最小二乘法,又是一个即熟悉又陌生的名字。对于学工科的我,简直就是听着最小二乘长大的(汗。。。)。但是,之前碰到要用最小二乘法的时候,我采取的办法都是拿来主义(抄。。。),并没有系统的了解一下什么是最小二乘法。包括最小二乘这个叫法,也从来都不理解(一直以为是一个外来词汇的音译翻译。。。)。所以,每次碰到最小二乘法,都是一脸懵bi。再加上拖延症(其实就是懒。。)作祟,最小二乘就像神一般的存在我的脑海中。直到有一天(此处省略500字。。。。),于是有了本篇文章。
1.引言
言归正传,在此先列举一下最小二乘家族成员。最小二乘法直线拟合,最小二乘法多项式(曲线)拟合,机器学习中线性回归的最小二乘法,系统辨识中的最小二乘辨识法,参数估计中的最小二乘法,等等。由此可见,我们每次碰到的都是最小二乘法这个多面体的其中一个面。如果只从单个面研究,就看不到它的整体,也就不能理解它的内涵。因此,为了搞明白这个多面体,我们就要从它的核心入手,剖析它最本质的内容。
先从最小二乘的名字来看,所谓最小二乘,其实也可以叫做最小平方和。那么,是什么的平方和最小呢?那肯定是误差最小,那是什么的误差呢?就是目标对象和拟合对象的误差。连起来看,就是通过最小化误差的平方和,使得拟合对象无限接近目标对象,这就是最小二乘的核心思想。可以看出,最小二乘解决的是一类问题,就是需要拟合现有对象的问题。这么看来,是不是也就可以理解为什么最小二乘应用如此广泛了呢。
2.最小二乘法解析
解释完了最小二乘的思想,下面就具体说一说最小二乘的方法(方法其实是将思想具体化)。从最小二乘思想中,我们可以提出以下几个问题。
1. 怎么列出误差方程?
2. 怎么最小化误差方程?
3. 怎么验证结果的准确性?
最小二乘法的核心,其实就是针对上述提出的三个问题的解法。
除此之外,还有一个重要的内容:
最小二乘应该说是一种思想,而只有结合了具体对象,才变成最小二乘法。这也就导致了多种多样的最小二乘公式、推导、证明等等。但是,其核心是最小二乘的思想,只是展示形式不同。那么,这个不同在哪里呢?
用一句话来说:基底不同。那么什么又是基底呢?
上式中的x1,x2,.....,xn就是基底。对于曲线拟合而言(见后面应用部分),x1=1,x2=x,x3=x^2.....。对于其他应用而言,x的含义又有所不同。看到这里,可能大家有一个疑问:都说最小二乘求解的是线性问题,为什么曲线拟合方程中出现幂次方这个非线性的环节了呢?
这就又涉及到了一个重要概念,那就是:所谓线性方程,是有针对的对象的,也就是有所指的。就像一个坐标点(x,y),其含义是针对x坐标轴和y坐标轴而言的。那么这里,对于曲线拟合过程。虽然方程针对x是非线性的,但是针对各个参数θ而言,这个方程就是线性的了。那么,如果所求是x,那么就无法用最小二乘法。换句话说,如果针对所求参数,方程是线性的,那么就可以使用最小二乘法求解。
2.1.误差方程
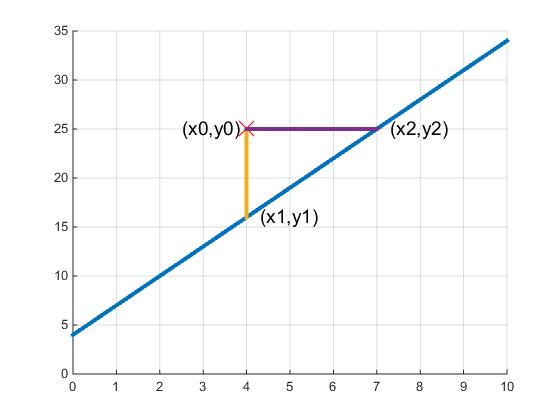
先说误差方程,就是用目标函数减去拟合函数,再取其平方即可。这里又涉及到一个问题,为什么要取平方和?如果不取平方和,取误差的绝对值之和,会有什么效果呢?可以从几个方面理解这个问题,先从几何的角度看这个问题。假设有一条直线y=ax+b,要在这条直线上找到一点,距离(x0,y0)这个点的距离最短。如果用绝对值的方法寻找,也就是取min(|y-y0|+|x-x0|),由于绝对值最小为0,所以最小的情况就是x=x0或者y=y0处,如下图1所示。
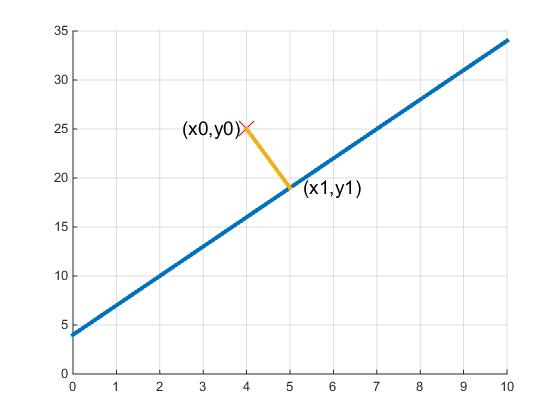
如果用平方和的方法寻找,就是取 ,可以看出该式是两点间距离公式,也就是距离的概念。那么最短的距离,就是点到直线的垂线,如下图2所示。
注:忽略纵轴与横轴的比值,在此只是示意图。
因此,相比于绝对值的方法,平方和的方法可以得到更短的距离,使得拟合函数更接近于目标函数。其实上述例子,就是从范数的角度考虑这个问题,绝对值对应的是1范数,最小二乘对应的就是2范数。此外,据说还可以从极大似然法中推导出平方和的公式,有兴趣的可以深入探究一下,我再次就不再赘述(其实我也没研究过。。哈哈。。)
2.2最小化误差函数
从高中我们就学过如何取极值,只不过不同于此的是,求取对象是一个一元二次方程。而最小二乘的误差函数形式多样,但其解决方法与求一元二次方程极值的方法相同。无非就是将原来对变量求导,变成了对向量求偏导(就是在向量某一个维度上的导数)。如果不是对向量求导,而是对函数求导,就是复变函数的变分法(可见都是换汤不换药,思想不变,重要的区别是求导对象不同)。求导之后,就是另求导的式子为0,解出极值点。再判断该极值点是极大值点还是极小值点,这样就得到了使误差函数最小化的向量值。到此,就完成了最小二乘法,是不是很简单呢。
2.3最小二乘的统计特性
如果只考虑应用,这部分的内容就不需要了解了。因为最小二乘的统计特性是探讨,最小二乘结果可靠的原因,需要用到随机过程这个工具,推导出最小二乘适用的原理。为了不让大家迷惑,以后单独探讨这个问题。
3.最小二乘法证明举例
已有N组{x,y}的数据,利用函数y=f(x;theta)去拟合数据,求当theta为何值时,拟合的效果最佳。
注:由于最小二乘法的应用场景多种多样,所以很多推导公式都是基于特定应用对象的。如遇到曲线拟合的问题,各参数基底是x的幂次方。在推导的过程中,就会出现范德蒙德矩阵,经常让人一脸懵逼。为了更简便的学习最小二乘推理过程,建议大家采用本文中的全部用符号替代所有参数基地,这样反而使得推导过程更加清晰。
3.1误差函数
3.2误差函数求偏导
针对误差和求偏导,有如下方程:
此处使用线性方程f去拟合数据。将上式经过化简整理,写为矩阵形式如下:
再结合 ,将上式每一行展开,再纵向求和,代入化简(化简过程比较繁琐,不过自己推导一遍会加深理解,有兴趣的可以自己推导一下,竟然可以将上式化简为非常简单的形式,很神奇)后可以得到如下方程:
注:下面公式(2)应为公式(1)
从以上计算可以看出,矩阵形式跟方程形式的最小二乘法是等价的,只不过是书写形式不同。如果直接从矩阵形式推导,可以更简便的得到结果(6)。特别注意,不可以直接用如下方法:
貌似这样得到的结果与我们计算得到的一样,但是其实是错误的。因为第一步Y=XA就是错误的,只有当误差项为0的时候,才可以这么写,否则的话存在误差项。
4.最小二乘法应用分析
4.1直线拟合
如果将最小二乘法中向量的维数设置为2,即(xi,1),拟合函数为y=ax+b,参数theta为2维,化简后的公式就是我们在书本上常见的直线拟合公式。
4.2曲线拟合
如果将最小二乘法中x,设置为如下形式:
最小二乘法就变成了曲线拟合公式。
4.3线性回归
机器学习中的线性回归算法,就是上面举例使用的公式。其中,线性代表的是拟合函数的形式,回归也可以称为拟合(起名问题都是历史遗留问题,哎。。)。在线性回归中,往往还经常听到一个名词,叫梯度下降。这种方法经常在如下情况使用,当XTX的逆无法求得的,也就无法用矩阵形式得到最小二乘的解。那么,就可以利用梯度下降的方法逐步的逼近出最优解。梯度下降可以算作解最小二乘的方法,跟矩阵解法、方程解法并列。具体区别可以参看知乎上对该问题的解释:
https://www.zhihu.com/question/24900876
4.4系统辨识中的最小二乘
就是将拟合函数用传递函数的时域表达式写出,通过输入输出数据,最终计算得到时域表达式中的各项参数,就实现了系统辨识。





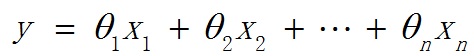

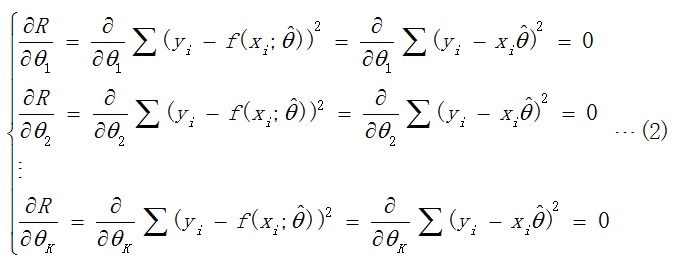
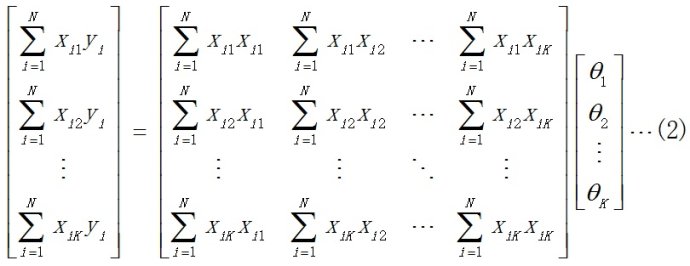

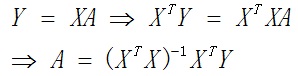
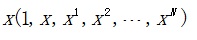
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








