基于树莓派的4D光场相机阵列

基于树莓派集群的灵活可扩展4D光场相机阵列构建

1 引言

1.1 捕捉4D光场

在三维（3D）空间中，光场或全光函数描述了光线在每个点沿所有方向传播的辐射度[2]。正如计算机图形学领域在可视化3D场景中成功探索的那样，四维（4D）光场函数L(u, v, s, t)表示自由3D空间中光线的辐射度，通常使用两个不同平面上的一对点(u, v)和(s, t)作为参数[10,12]。尽管光场的概念已有效应用于包括三维图形、计算机视觉和计算测光等多个领域的实用系统中，但从真实世界获取光场数据仍是一个具有挑战性的问题。生成四维光场的一种有效方法是使用专用的光场相机，也称为全光相机。自从提出在像平面上使用柱状透镜阵列来采集镜头光圈不同子区域入射光的光场相机以来[3]，已有若干构建可行光场相机的尝试，相关内容将在相关工作部分讨论。其中一些努力取得了成功，并推动了商业光场相机的生产[16,20]。

1.2 我们的贡献

在本研究中，我们提出了一种新的光场相机原型，其主要关注点在于简洁性和开放性。主要贡献在于，与以往方法不同，普通用户可利用常见且廉价的树莓派计算机轻松组装定制的光场相机。所提出的相机系统结构灵活，可根据用户对相机性能的需求（例如，视场角和4D光场图像的分辨率）进行重新配置。该原型还具有可扩展性，只需添加额外的组件即可扩展其功能。此外，通过用更新的树莓派系统的主板和/或相机模块进行替换，可以轻松升级相机系统，以增强其光线捕捉能力和性能。需要注意的是，使用紧凑且低成本的树莓派系统，有可能构建出体积更小的相机，生成比以往光场相机（例如[26–28]）分辨率更高的4D光场，而无需像以前那样依赖任何额外定制设计的硬件单位（例如[9,18,24,26,28]）。

为了展示我们使用树莓派系统构建DIY 4D光场相机的方法的有效性，我们构建了一个使用 10×10树莓派相机模块阵列来捕获原始图像的系统。在我们的系统中，各个相机模块分别连接到专用的Raspberry Pi主板，这些主板通过Wi-Fi网络由主机PC控制，同时将捕获的非平凡尺寸图像通过稳定且高速的有线网络传输到主机PC。除了硬件系统外，我们还开发了一种鲁棒的相机校准方法，能够从捕获的原始图像生成有效的4D光场。此外，我们在GPU上设计并实现了一个虚拟相机模型，旨在从获取的4D光场中创建多种摄影效果。

本文其余部分结构如下：在第2和3节回顾相关工作和基础理论之后，我们将在第4和5节中说明我们的光场相机系统的设计与实现。在第6和7节中，我们将展示我们的GPU辅助光场渲染器如何高效地处理所获取的4D光场，以交互方式合成诸如缩放和平移、重新对焦、焦点呼吸效应和景深等有趣的视觉效果。最后，第8节总结全文并探讨未来方向。

2 相关工作

在2000年初期，出现了多种构建密集相机阵列的方法，旨在生成各种类型的光场。吴等人[27]构建了一个由 8 × 8低成本视频相机阵列组成的分布式相机系统，每个相机以平均每秒18帧的帧率录制 320 × 240像素视频。有趣的是，该光场相机展示了重新对焦能力；然而，在生成景深效果时，渲染图像中包含烦人的伪影，这主要是由于相机数量不足和低图像分辨率所致。

张和陈[28]构建了一个由48个相机组成的相机阵列，其排列可以轻松重新配置以提高整体渲染质量。虽然通过渲染示例展示了利用可重构相机阵列进行视点相关图像捕获这一想法的有效性，但他们仅将该系统应用于从移动视点观察的图像生成，而未引入任何合成镜头效果。威尔伯恩等人[26]也使用定制硬件组件构建了一个可重构相机阵列，能够以高帧率录制640像素视频。特别是当采用配备广角镜头的相机时，该相机系统能够成功模拟合成孔径摄影。针对由多兆像素相机组成的光场相机系统，文卡塔拉曼等人[24]最近将相机阵列集成到单个单片传感器基板上，并结合集成透镜阵列，其尺寸足够小，可安装在移动设备上。林等人[15]最近还实现了在光场显微镜[13]中使用相机阵列对光的空间和角度分布进行采样的想法。

除了这些相机阵列系统外，还出现了构建手持式光场相机的尝试。吴等人[18]提出了一种全光相机，通过在成像传感器和主镜头之间放置微透镜阵列，在单次拍摄曝光中对四维光场进行采样。利用所采集的光场，他们证明了通过对虚拟镜头孔径的有效采样，可以实现更高质量的合成孔径效果，例如重新对焦和景深（另见[17]）。另一方面，乔治夫等人[9]提出了一种设计方案，通过将透镜和棱镜系统附加到传统相机上构建出有效的光场相机。当结合基于计算机视觉的算法时，他们报告称其相机在计算图像中可实现 700 × 700像素的高空间分辨率。与这些基于光学重采样的方法相比，后者通常强制在空间分辨率和角度分辨率之间做出固定权衡，而一些灵活技术已被提出用于构建能够采样更高品质4D光场的光场相机[14,23]。

最后，树莓派是一种运行基于Linux的操作系统的微型单板计算机，最初由树莓派基金会开发，旨在促进学校中的基础计算机技术和编程教育[8]。自2013年首款型号问世以来，树莓派计算机的几代产品已陆续发布，其应用领域迅速扩展，包括游戏、集群计算、家庭自动化、网页浏览和机器人技术等。本文表明，树莓派计算机还可有效用于构建可根据用户需求进行易于重新配置的DIY四维光场相机系统。

3 前期工作

3.1 相机参数估计

相机标定是估计相机模型参数以生成给定照片的过程，其中从世界空间到图像坐标系的映射通过一个相机矩阵进行近似，通常还包括畸变系数[11]。相机矩阵表示为两个矩阵的乘积，分别描述相机的内参和外参。

3 × 3内参矩阵MI，即从相机空间到图像坐标系的映射，由焦距fx和fy、主点偏移(cx, cy)以及轴倾斜系数γ组成。

$$
MI= \begin{bmatrix}
f_x & \gamma & c_x \
0 & f_y & c_y \
0 & 0 & 1
\end{bmatrix}
$$

与对于给定相机保持不变的内参矩阵不同，3 × 4外参矩阵ME包含了相机在世界空间中的具体位置和方向；因此，它通过平移T和旋转R来表示，从而实现从世界空间到相机空间的变换：

$$
ME= \begin{bmatrix}
r_{11} & r_{12} & r_{13} & t_1 \
r_{21} & r_{22} & r_{23} & t_2 \
r_{31} & r_{32} & r_{33} & t_3
\end{bmatrix}=[R | T]
$$

一旦估计出这两个矩阵，我们就能在世界空间 $(x_w, y_w, z_w)$ 和图像坐标 $(u, v)$ 之间转换点

$$
\begin{pmatrix}
z_c u \
z_c v \
z_c
\end{pmatrix}= MI \cdot ME \cdot
\begin{pmatrix}
x_w \
y_w \
z_w \
1
\end{pmatrix},
$$

其中zc表示点沿主轴的深度。除了这些矩阵外，我们通常还需要处理用于校正镜头畸变的额外参数，该校正通常通过径向(k1,k2,k3)和切向畸变系数(p1,p2)[5]来实现

$$
(u_{corrected}, v_{corrected}) = (1+ k_1 r^2 + k_2 r^4 + k_3 r^6)(u, v) + (2p_1 uv + p_2(r^2 + 2u^2), p_1(r^2 + 2v^2))
$$

3.2 光场数据的应用

在光场渲染中通常如[10,12]所述，待获取的四维光场的辐射度L(u, v, s, t)通过由两个不同（不一定平行）平面上的两点(u, v)和(s, t)所定义的光线进行参数化，其中坐标被归一化，使得(u, v)和(s, t)均位于单位正方形内[0, 1]×[0, 1]（见图1）。那么，在成像平面上形成的图像强度与通过给定镜头孔径接收到的入射光的照度成正比。已知成像点处的照度E(s, t)可表示为在镜头区域上对辐射度L(u, v, s, t)的加权积分。

$$
E(s, t)= \frac{1}{f^2} \int\int L(u, v, s, t) \cos^4 \theta \, du \, dv,
$$

其中f为焦距，θ是光线(u, v, s, t)与成像平面法线[22]之间的夹角。

一旦通过光片成功采样得到四维光场数据集，便可从中有效重现多种有趣的渲染效果，例如视图变换[10,12]、重新对焦[18]、景深控制[25]。例如，可通过应用合成摄影方程，从以焦距f拍摄的光场数据生成在新焦距f′处重新对焦的图像

$$
L_{f’}(u, v, s, t)= L_f(u, v, u+ \frac{s - u}{\alpha}, v+ \frac{t - v}{\alpha})
= L_f(u, v, u(1 - \frac{1}{\alpha}) + \frac{s}{\alpha}, v(1 - \frac{1}{\alpha}) + \frac{t}{\alpha}),
$$

其中 $\alpha= \frac{f’}{f}$。

如果忽略E(s,t)中的$\cos^4 \theta$项并近似为1，则照度图像值简化为

$$
E(s, t)= \frac{1}{\alpha^2 f^2} \int\int L_{f’}(u, v, s, t)\,du\,dv,
$$

对于每个图像像素(s, t)，随后在离散化的(u, v)空间上使用数值积分技术进行近似。请注意，尽管上述积分通常假设uv平面与镜头光圈平面重合，但本文实现的虚拟相机可以在世界空间中的任意位置和方向放置，这一点将在后文展示。

4 4D光场相机的构建

图2显示了我们开发的相机系统，主要由安装在三脚架上的 10× 10树莓派相机模块阵列和一个容纳100块树莓派1型B款主板的集群组成，该集群置于一个专门设计的亚克力支架中。每个树莓派相机模块（v.1.3）均采用固定焦点镜头，其景深范围从1米到无穷远，并配备OmniVision的500万像素CMOS传感器（OV5647），可输出 2592× 1944像素。该镜头的焦距为3.60毫米，结合 3.76× 2.74毫米的传感器成像面积，可提供大约 53.50度（水平）和41.41度（垂直）的视场角。

如图3所示，我们试图将相机尽可能紧密地排列在一起，以生成高分辨率的四维光场。由于相机模块的尺寸限制，相机阵列中相邻两个镜头中心之间的距离设定为28 mm；因此，相机阵列的有效面积为 280×280mm。阵列中的各个相机模块具有相应的地址(i,j), i,j= 0, 1,…,9，其中最左下角的为(0, 0)。一条15针带状电缆将固定在阵列上的每个树莓派相机板连接到专用树莓派板上对应的15针MIPI摄像头串行接口(CSI)连接器。

这100台树莓派计算机通过Wi-Fi网络无线连接到一台主机PC，由该主机PC控制整个相机系统。为了有效同时管理这100台计算机，我们使用安全外壳网络协议实现远程命令执行，以便轻松访问树莓派系统类Unix操作系统上的shell账户。主机PC的主要任务是发送启动图像捕捉的命令，并将捕获的原始图像收集到存储系统中。当100个相机模块完成图像捕捉后，原始图像通过有线局域网从100台树莓派计算机经由三台机架式网络交换机（TP-Link TL-SF1048）传输至主机PC，每台交换机最多支持48个10/100Mbps RJ45端口，每次传输通常耗时不到一分钟。

在当前实现中，相机模块被均分为两组。图像拍摄来自主机PC的命令通过先捕获第一组相机对应的图像，然后暂停约半秒，再捕获剩余图像的方式来执行。原因是当整个100台相机阵列同时工作时，相机模块与树莓派板之间的排线电缆会出现间歇性过强的信号干扰，导致图像噪声不规则。虽然通过分两步拍摄的方式已解决此问题，但该问题仍有待在未来彻底解决。

5 校准的4D光场的生成

5.1 在世界空间中设置四维光场

为了能够从相机阵列捕获的原始图像集合中生成有效的四维光场数据集，需要将四维光场L(u, v, s, t)的归一化参数空间适当地映射到真实世界。在我们的相机系统中，空间映射由棋盘格与相机阵列之间的相对位置定义（见图4）。

首先，我们使用一个方形棋盘格来定义一个右手三维世界坐标系，其中xw轴和yw轴分别平行于棋盘格的两个正交边，且其左下角位于原点。此处，棋盘格区域对应于四维光场参数空间中[0, 1]×[0, 1] st平面上的区域，该区域定义了视窗view window，相机阵列中的每个相机通过该视窗观察真实世界。

其次，当放置相机阵列时，相对于世界空间确定一个点 pca 和三个正交归一化向量 uca、vca 和 nca，类似于棋盘格的情况。其中，相机阵列区域被称为PRP窗口，因为它包含了相机模块的投影参考点。很自然地，映射到归一化参数空间中uv‐平面上[0, 1] ×[0, 1]区域的PRP窗口与视窗平行。然而在实际操作中，拍摄时只需尽量将棋盘格和相机阵列放置得相互平行即可。在此设置下，每个相机模块的相机中心，即投影参考点eij，被设计为在相机阵列中均匀分布。因此，我们可以认为所捕获的图像已经在uv‐平面上对PRP窗口区域进行了均匀采样。

在探索所捕获的图像数据以进行光场渲染之前，必须完成两项任务。首先，每次相机阵列相对于棋盘格的位置发生变化时，都需要通过校准过程重新计算几何参数pca、uca、vca和nca，该过程将在稍后说明。其次，对每个相机模块捕获的原始图像进行重采样，使所得图像在st平面上的视窗内实现规则采样，从而完成均匀采样的离散4D光场数据集的生成。

5.2 我们相机系统的校准过程

5.2.1 4D光场的离散参数空间

尽管可以采用不同的配置，但为了说明起见，我们假设相机系统使用一个 10×10相机阵列，并且视窗区域以 ns × nt的分辨率进行采样。因此，uv‐平面上的单位正方形在(ui, vj)=( i+0.5 / 10, j+0.5 / 10), i, j ∈[0, 9]处进行采样，其在世界空间中的位置eij可利用几何参数pca, uca, vca和nca轻松生成。另一方面，st平面上的单位正方形在(sk, tl)=( k+0.5 / ns, l+0.5 / nt ), k ∈[0, ns − 1], l ∈[0, nt − 1]处进行采样，其位置通过棋盘格的实际尺寸缩放至世界空间。需要注意的是，与PRP窗口不同，均匀采样的视窗空间的定义域可能大于单位正方形 [0, 1]×[0, 1]，只要所捕获的图像能够提供适当的颜色信息即可。（例如，如果可能的话，我们可以拥有像 [−1.2, 1.2] ×[−1.2, 1.2]这样的st域。）因此，在给定配置下，校准过程后获得的离散4D光场数据集表示一幅4D图像L(ui, vj, sk, tl)。

5.2.2 估计PRP窗口的几何参数

校准我们相机系统的第一子步骤是估计参与的相机模块的内参。然后通过估计每个相机的外参矩阵来确定其位置和方向在世界空间中获得。我们使用OpenCV库提供的函数执行了这些基本的相机标定过程[19]。理论上，相机的投影参考点估计值应在世界空间中的同一平面上。然而，由于系统构建和相机标定时引入的各种数值误差，这些参考点通常会在数值上偏离单一公共平面。尽管这些偏差通常很小，但在光场渲染阶段往往会带来困难，尤其是视觉上的问题。为了尽可能避免这些问题，我们通过以下校准过程来估计相机在世界空间中的 “最佳”位置以及PRP窗口的几何参数。

设(xij,yij,zij)为通过外参标定获得的第(i,j)个相机位置的世界空间坐标，i,j ∈[0, 9]。那么，对于一个假设包含所有相机中心的世界空间中的平面P(x, y,z)=ax+ by+cz+ 1= 0，我们得到如下超定线性系统，其中相机以任意顺序编号为ncam= 100：

$$
\begin{bmatrix}
x_1 & y_1 & z_1 \
x_2 & y_2 & z_2 \
\vdots & \vdots & \vdots \
x_{100} & y_{100} & z_{100}
\end{bmatrix}
\begin{bmatrix}
a \ b \ c
\end{bmatrix}
=
\begin{bmatrix}
-1 \ -1 \ \vdots \ -1
\end{bmatrix}
$$

对于使用最小二乘逼近方法得到的最优平面P∗(x, y, z)= a∗x+ b∗y+c∗z+ 1= 0，令P∗ij表示第(i,j)个相机投影到该平面上的世界空间位置。理想情况下，世界空间中新的相机位置应位于最优平面P∗(x, y,z)= 0上规则网格单元的中心，以此表示我们在世界空间中的相机阵列，因为我们的相机阵列正是如此设计的。由于数值精度问题，估计出的位置通常不会精确地与网格对齐。在构建我们的相机阵列时，我们在最优平面上放置了一个 10 × 10规则网格，以最小化投影后的相机中心的偏差。

为简化计算，考虑一个由投影后的相机中心的质心以及两个主方向定义的二维(2D)坐标系(x,y)：首先将世界空间的xw‐轴投影到最优平面上以确定x‐轴方向，然后计算与其正交的方向作为y‐轴方向（参见图5中的新坐标系）。然后，令P∗ij =(x∗ij ,y∗ij )t表示 ˆP∗ij在新二维空间中的坐标。

‐相机在二维空间中的投影位置，而Pij是(i,j)‐网格单元的中心。此外， ¯Pij表示由待估计的未知刚体运动变换后的点Pij)

最初，在尺寸为 280 × 280mm的PRP窗口区域中放置了一个 10 × 10均匀网格，将二维空间中的网格调整，使其中心与原点重合（见图5左侧的网格），其中网格的(i,j)号单元格的中心记为Pij=(xij,yij)t。然后通过刚体变换M(α, β; θ)= T(α, β)R(θ) so¯在平面上调整该网格，使得Pij与P∗ij¯之间的平方距离之和最小，其中Pij是变换后Pij的位置。这可以通过求解使平方和最小的刚体运动的平移（α∗和 β∗）和旋转（θ∗）位移来实现（最优位移估计的详细方法参见附录）。

请注意，包含世界空间中PRP窗口的最优平面P∗(x,y,z)= 0的法向量决定了单位向量nca（再次参见图4）。然后，PRP窗口的其余几何参数pca, uca和vca可轻松从指定相机阵列相对于最优平面的最优位置和方向的参数(α∗, β∗; θ∗)中获得。

5.2.3 重采样原始图像

生成最终四维光场数据集L(ui, vj, sk, tl)的最后一步，是在视窗上对在(ui, vj), i,j ∈[0, 9]处捕获的每幅图像，在均匀分布的采样点(sk, tl), k ∈[0, ns − 1], l ∈[0, nt − 1]处进行重采样。包含PRP和视窗的两个平面通常并不完全平行，这意味着相机模块的物理成像平面与视窗的物理成像平面不平行。因此，首先使用OpenCV库计算匹配两个平面上点的平面单应性矩阵，并为该相机创建一幅均匀采样的ns × nt图像。

基于树莓派集群的灵活可扩展4D光场相机阵列构建

6 光场渲染

6.1 用于光场渲染的虚拟相机模型

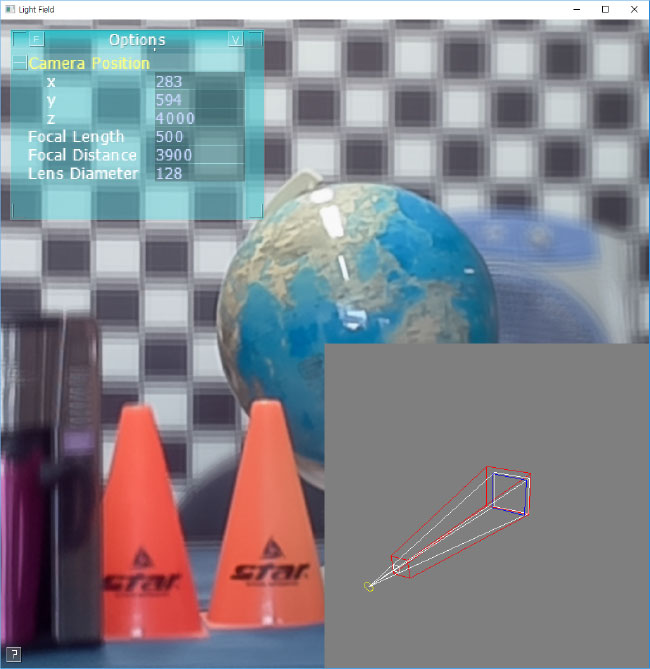
为了有效渲染采集到的4D光场数据集，我们定义了一个虚拟相机，由用户交互式操作。首先，在世界空间中通过一个点ec来指定相机坐标系，该坐标系决定了相机的外参，该点表示相机空间的原点，即相机的投影参考点，以及三个正交归一化向量uc、vc和nc，分别表示相机空间的xc、yc和zc轴，其中相机朝向负zc轴方向，类似于OpenGL系统（见图6）。

其次，关于内参，我们模拟中画幅胶片摄影，尽管其他格式也是可能的。具体而言，我们采用120胶片格式，其实际图像尺寸为 56× 56mm。因此，(i) 当用户选择焦距 f（单位：mm）作为虚拟镜头参数时，视场角 θf（单位：度）或无限对焦时的视角被设置为 θf = 2 tan⁻¹(56/(2f))。接下来，(ii) 如果用户通过设置对焦距离 do（即镜头与完全合焦的（假想）物平面之间的距离）来对相机进行对焦，则放置正交于zc轴的虚拟胶片平面于zc = di处，其中心点位于zc轴上，而像距 di则根据薄透镜公式 1/di + 1/do = 1/f 确定。

为了控制渲染图像中的景深，(iii) 用户还需设置光线通过的有效镜头孔径的直径 dl（单位为 mm）。实际相机的孔径通过f数进行调节，该值是焦距与入瞳直径的比值。我们允许用户直接指定直径 dl，因为它能更直观地反映镜头孔径相对于所渲染的四维光场的相对大小。

默认情况下，我们的虚拟相机模型会自然产生焦点呼吸效应，即当对焦距离改变时视场角发生的变化。因此，正如在传统的单镜头系统中观察到的那样，通过移动镜头或传感器（焦距固定）实现对焦时，当对焦更近（更远）时，视场角会变得更窄（更宽），其中根据薄透镜公式，对应于对焦距离 do 的新视场角变为 θfov = 2 tan⁻¹(56(do−f)/(2f do))。在我们的虚拟相机系统中，我们也允许(iv) 用户选择性地启用无呼吸效应模式，在该模式下，无论物距如何变化，有效视场角保持不变，这类似于某些昂贵镜头中的设计。该模式通过固定镜头与虚拟胶片之间的距离来实现，此时在对焦更近时，有效焦距会缩短。具体而言，可以很容易地证明，当有效焦距 fe = f · do / (do + f) 保持不变时，视场角将保持恒定，其中 f 是镜头的焦距。

6.2 对胶片和镜头光圈的采样

在渲染时对虚拟胶片上的某一点进行采样时，镜头光圈区域也会使用一组点样本进行随机采样，在我们的实现中，这些点样本是基于同心映射的圆盘采样方法生成的[21]。对于胶片上的给定采样点（再次参考图6），根据薄透镜理论，生成一组对应于镜头光圈上采样点的光线：首先将连接胶片采样点与镜头中心的直线与焦平面相交，得到一个参考点 po，然后从每个镜头采样点穿过 po 生成相对于世界空间的光线，从而形成一组光线样本。

每条光线采样与存在于世界空间中的四维光场的光片相交，以获取辐射函数L的(ur, vr)和(sr,tr)坐标。为了从四维光场数据集中获取合适的辐射值L(ur, vr, sr, tr)，需要应用适当的滤波操作。尽管存在其他成本较低的方法，例如最近邻与双线性滤波器的组合，但我们发现，对完整4D函数进行计算代价最高的四线性滤波在GPU实现中仍然足够快速。在通过这些采样光线从四维光场中收集所有辐射值后，使用加权平均法确定胶片采样点的最终辐射值。

请注意，当我们使用微小孔径模拟pinhole camera时，镜头的中心即投影参考点ec，成为镜头上唯一的采样点。例如，如果要使用视场角为 θf 的虚拟相机渲染 1024×1024像素的图像，则可以从反转图像左下角开始枚举像素，计算从第(i,j)个像素中心出发的光线Rij(t)=ec+ t · rij的方向rij，该方向可在世界空间中计算得出

$$
\mathbf{r}_{ij} = -\mathbf{n}_c + \tan\left(\frac{\theta_f}{2}\right)\left(\frac{2i+1}{1024}-1\right) \mathbf{u}_c + \tan\left(\frac{\theta_f}{2}\right)\left(\frac{2j+1}{1024}-1\right) \mathbf{v}_c.
$$

另一方面，当镜头的孔径直径不为零且为dl > 0时，针对每个胶片采样点，需处理与镜头区域成正比数量的镜头采样点对应的光线。虽然这会增加每次渲染所需的计算时间，但能自然地产生重新对焦和景深控制等效果。

7 实验结果

为了验证所提出方法的有效性，我们构建了一个如前所述的4D光场相机系统，并测试了其性能。所有软件实现和性能评估均在一台配备Intel Core i7-5960X CPU、64GB主内存以及Nvidia GeForce GTX 1080显卡（8GB显存）的PC上进行。GPU编程使用OpenCL 1.2 API实现[1]。

所开发的系统包含三个主要组成部分：
– 由 10× 10个相机阵列组成的相机系统，每个相机模块通过 CSI 连接器连接到专用的 Raspberry Pi 主板（见图2），
– 从捕获的原始图像生成校准后的 4D 光场数据集的系统软件，以及
– 实现有效光场渲染的应用软件。

7.1 图像采集与校准

。a左下(0, 0)，b右下(0, 9)，c左上(9, 0)，以及d右上(9, 9))

图7展示了使用我们的相机系统捕获的示例四维光场数据集的四幅原始图像。为了对该示例数据集进行相机系统校准，我们将定义世界坐标系的棋盘格放置在相机阵列前方约3.6米处。（注意：原始图像中的棋盘格仅仅是场景中的一个物体，而用于校准过程的棋盘格大致放置在标记锥体的距离处。）在拍摄过程中，来自相机阵列的每幅分辨率为 2592× 1944像素的原始图像均以最高质量的 JPEG 图像保存为文件。每幅原始图像的大小约为2.7兆字节；因此，每次图像捕获过程存储所有原始图像所需的总硬盘空间约为270兆字节。

当通过所述校准过程从原始图像数据生成分辨率为 10 × 10 ×1248×1152的四维光场数据集时，最终二进制数据加载到主存/显存中的大小为411.3MB，用于光场渲染。图8展示了生成的四维光场函数在图7中所述四个角点处的2D切片(0.05, 0.05,·,·)：左下为 L(0.05, 0.95,·,·)，右下为 L(0.05, 0.95,·,·)，左上为 L(0.95, 0.95,·,·)，右上为 L(0.95, 0.05,·,·)。

，b右下角(0, 9)，c左上角(9, 0)，以及d右上角(9, 9))

在生成光场数据集的过程中，我们意外发现所使用的老旧相机模块在清晰度、亮度和白平衡方面常常无法产生一致质量的图像，这一点可以从图8的四个样本图像中识别出来。我们希望使用更新版本的相机模块能显著缓解这一质量问题。

7.2 光场渲染及其性能

图9展示了该应用程序软件用户界面的快照，用户可通过该界面控制各种相机和渲染参数，以交互方式从校准的光场数据集中生成渲染图像。开发高效光场渲染器最重要的因素之一是充分利用渲染算法中固有的高度并行性，这使得在GPU上实现高效计算成为可能。

为了揭示使用GPU所带来的性能提升，我们首先测量了在CPU和GPU上计算图像所需的时间，该图像通过虚拟针孔相机生成，其中仅在镜头区域的中心采样一个点。

分辨率	CPU (ms)	GPU (ms) (8,8)	GPU (ms) (16,8)	GPU (ms) (16,16)	GPU (ms) (32,16)
768×768	289.84	1.56	1.34	1.41	1.68
1024×1024	510.41	1.62	1.53	1.91	2.05
1536×1536	1149.38	2.83	2.73	3.15	3.34
2048×2048	2023.93	4.04	3.87	4.79	4.87

表1 虚拟针孔相机的渲染时间（单位：毫秒）。GPU时间中括号内的数对表示OpenCL内核所采用的工作组大小。我们观察到GPU上渲染时间显著减少，其中最佳耗时以粗体标出

生成图9中透视视图所需的 CPU 和 GPU 时间在示例 4D 光场数据集的分辨率上进行了比较。正如直观所见，渲染时间为基本上与单线程CPU程序运行时渲染图像的图像像素数量成正比。然而，正如预期的那样，GPU上的OpenCL实现实现了显著的加速，其计算时间随图像像素数量呈亚线性增长，这表明GPU在处理更大规模的并行任务时具有更高的效率。特别是，我们观察到通常在OpenCL工作组大小为(16, 8)时，GPU上获得最佳性能；因此，该配置被应用于我们的整个并行渲染器中。

图10展示了使用具有非零光圈直径的虚拟镜头所获得的部分渲染结果（另见图11中的另一个示例数据集）。在渲染这些分辨率为 1024×1024像素的图像时，应用了四线性滤波器从4D光场数据中获取辐射值。在图10a的图像序列中，焦距和光圈直径保持固定，而对焦距离发生变化。在默认模式下，随着对焦平面前后移动，产生了自然的呼吸效应。我们的虚拟相机还提供了无呼吸效应模式，如图10b所示，在该模式中，焦距会根据变化的对焦距离进行调整，以保持视场角恒定。

通过分别调整光圈直径和焦距，使用我们的虚拟相机还可以轻松生成景深效果和变焦效果，如图10c、d所示。最后，对于此示例数据集，移动相机以获取图10e中的图像序列，该序列展示了显著的透视和视差变化以及轻微的景深效果。请注意，只要虚拟相机的视景体与4D光场块覆盖的区域有足够的相交，我们的系统中的虚拟相机就可以在世界空间中自由移动，具有任意的位置和方向。

所有这些精美的镜头效果并非轻易获得，因为与针孔相机不同，每个图像像素都需要对镜头上的多个点进行采样。在我们的实现中，我们将镜头采样数nls设置为与虚拟镜头面积和镜头采样率均成正比，以便用户能够直观地控制各种镜头效果的质量。更具体地说，镜头采样大小定义为nls= γ ls² / (2¹⁰ π) · π(dl/2)²，其中分母中的项 2¹⁰π是一个归一化因子，反映虚拟镜头的物理尺寸。

光圈直径 (dl)	镜头采样率 (γls) 1.0	2.0	4.0	9.0	16.0
64毫米	2.67	4.83	6.06	11.74	19.41
128毫米	4.22	6.62	11.56	23.38	40.82
192毫米	6.04	10.38	18.33	39.25	64.06
256毫米	7.81	14.01	25.88	60.61	87.38

表2 GPU上的光场渲染时间（单位：毫秒）。生成图12a中视图的 1024 × 1024像素图像所需的时间（f= 444mm 且 do= 4000mm）。为了研究 GPU 上的计算负担，我们测试了不同的光圈直径和镜头采样率组合。通常，镜头采样率在 4.0 到 9.0 之间时可获得满意的镜头效果，其 GPU 时间以粗体突出显示

如表2所示，计算时间受到光圈直径和镜头采样率的显著影响。可以预期的是，渲染图像中失焦区域的散景质量由镜头采样率决定，它决定了镜头样本的密度。我们的实验表明，镜头采样率在4.0到9.0之间时通常能产生足够好的镜头效果，而不会过度增加渲染时间（见图12）。

的左下，位于(0, 9)的右下，顶部左下角位于 (9, 0)，右上角位于 (9, 9)。b各种镜头效果：无焦点呼吸的重对焦（前两张图像）、景深（中间两张图像）和平移（最后一张图像）)

8 结论与未来工作

本文介绍了一种基于树莓派计算机的相机系统，可便捷地捕捉四维光场。为了便于从采集的图像数据中进行光场渲染，我们提出了一种有效的校准和重采样过程，以生成与归一化4D空间对齐的4D光场数据集。我们还表明，通过调整所提出的虚拟相机模型提供的各种参数，可以从获取的4D光场中生成多种良好的镜头效果，例如重新对焦、焦点呼吸效应、景深以及缩放和平移。

我们的光场相机系统架构具有可扩展性和灵活性，能够轻松地根据用户需求进行定制。由于基于常见且价格低廉的树莓派计算机，该相机系统可以低成本构建，并能方便地升级到具有更强光线捕捉能力的新版本。

在构建相机系统时，我们遇到的一个意外困难是相机模块拍摄的原始图像质量存在问题，这进而对四维光场生成过程产生了负面影响。我们发现，较旧的500万像素相机模块（v.1.3，发布于2013年）所拍摄的图像往往不够清晰，并且各相机模块之间的亮度和白平衡不一致，从而对最终的4D光场渲染质量产生不利影响。我们认为，使用最近升级的800万像素模块（v.2.1）将有助于轻松捕获质量更高的4D光场。

目前，10 × 10相机阵列的配置仅提供有限的视场角。虽然在阵列中使用更多的相机模块或构建额外的相机阵列可以简单地扩大视野，但一个更有趣的解决方案是利用当前的相机系统捕获多个重叠的四维光场，然后将它们拼接在一起，生成具有更大视场角的集成光场数据集。需要注意的是，在相机阵列上附加一个配备RGB-D传感器的支持Google Tango的移动设备，将有助于估计拍摄序列中相对的六自由度相机阵列位姿，这对于生成覆盖更广泛三维区域的复合四维光场至关重要。未来的工作将涉及为此混合四维光场采集过程开发一种软件解决方案。

此外，当前系统尚不能生成光场视频。另一个有趣的研究方向是通过在现有的4D空间中增加时间维度来生成有效的五维（5D）光场，从而让用户能够通过光场渲染创建各种动画效果。尽管可以使用现有的树莓派相机模块轻松录制视频以获取5D光场的原始图像，但如何以紧凑形式表示重建的光场数据集并高效地进行渲染仍然是具有挑战性的任务。

最后，构建一个四维RGB-D光场相机系统仍是一项未来的工作，该系统可能仅使用少量用于静态场景的移动RGB-D传感器，或一组具备深度感知能力的树莓派相机模块，以增强传统4D光场并提供更精细的高质量深度信息（例如参考[7]所使用的）。此外，由于高分辨率且具有详细深度信息的光场已易于获得，因此开发适用于各种显示设备（包括裸眼3D显示）的适当光场渲染技术仍将是一个挑战（例如，参见[4]中为基于投影的光场显示器设计的渲染技术）。