水流驱动传感器网络监测管道泄漏

水流驱动的传感器网络用于输水管道中的泄漏与污染监测

帕拉·阿米唐舒和克里希纳·坎特，天普大学，美国

在本文中，我们提出了用于城市供水系统泄漏和污染监测的水流驱动的传感器网络的概念。本研究的独特之处在于，该传感器网络可部署于地下管网中，仅需通过人孔接入连接点，并且仅依靠水能采集驱动，无需交流电源或频繁更换电池。尽管水務系统可能受到多种污染物的影响，但实际可部署的传感器数量有限。因此，许多类型的污染物通过“代理感知”方式进行检测，而这种方式可能并非100%可靠。本文解决的主要问题包括：（a）自适应调整网络以利用可用能量，从而最大化泄漏/污染检测能力；（b）在自然水流几乎为零的时期，通过最小化的人工水循环或泄漏来提高检测能力。文章通过大量仿真表明，所提出的方法可显著缩短泄漏/污染报告时间（从3.5小时缩短至 ∼6分钟），并且通过自适应控制可将人工水循环减少 ∼33%，同时仍将采集和传输的数据量提升30%。

1 引言

供水系统（WDS）通过复杂的管道系统将淡水从水源和储水水库/水箱输送到工业、商业 和住宅区。然而，淡水资源持续减少，到2025年，全球三分之二的人口将面临水资源压力， 约25%的人口将经历严重的水资源短缺[1]。随着人口向城市地区迁移，城市水务系统的压力不断加剧，而大多数系统状况堪忧，存在大量水管泄漏、渗漏和污染问题[2]。传统的水质监测主要依赖人工操作[3]，对于大规模且高负荷的供水系统而言已显不足。因此，迫切需要开发基于信息与通信技术的解决方案，以比目前普遍采用的人工操作更低成本的方式检测和定位泄漏与污染。这一需求极为紧迫

检测还有助于延长这些系统的工作寿命，对于资金紧张的供水公用事业具有巨大价值。

本文的主要目标是开发一种传感器网络，用于持续监测水管中的水泄漏和污染，并将相关数据报告给控制站，以便进行检测与定位所需的分析。尽管该概念在理论上很简单，但由于以下环境限制，实现这一问题的有效解决方案极具挑战性：（a）大多数管道大多埋于地下，只能通过人孔的连接点进入；（b）人孔通常无法接入交流电源；（c）射频通信需穿透水、管材、土壤、岩石等介质，面临严重的衰减，因而需要高功率；（d）无法利用太阳能为传感和通信供电；（e）定期在人孔中更换电池可能非常昂贵。

为了解决这些问题，本文考虑水流驱动传感器网络（WDSN）[4,5]，其完全由水流通过小型水力风扇单元供电。我们采用小型超级电容器来存储采集的能量，主要原因是当前超级电容器具有较长的循环寿命和高充放电效率[6]。假设传感器节点仅位于管道连接点或阀门位置，通过人孔进行安装。其下部浸入水中，用于能量采集以及污染、流速等测量；上部则配备能量存储装置、升压器、稳压器以及计算/通信单元。我们假设上部配有合适的无线射频（例如WiFi），天线嵌入在已有的“智能”井盖外露侧[7]。实际上，传感器模块可能仅部署在某些特定连接点，例如仅大直径管道的连接处，或那些非常老旧或其他原因易发生泄漏或污染的位置。但为简化起见，我们将假设在每个连接点都进行部署。

由于管道中流速（由用水量驱动）的变化，采集能量的可用性在空间和时间域上均存在变化。在支管中，流量可能会显著波动，并在夜间较晚时段或其他特殊情况（如正常工作时间内家中人数极少）下降至接近零。因此，必须根据可用能量分布来自适应数据采集与传输。通过利用单个传感器节点的高度相关检测能力，我们提出了一种基于节点能量预算的动态采样与传输速率自适应方案。由于大多数供水系统都配备有可从控制室集中控制的水泵，因此可以通过将水从水库抽回同一或另一个水库，人工向系统内循环水。我们研究了此类循环在低自然流速期间保持网络运行的作用，从而提升污染/泄漏检测能力。

由于水可能以多种方式受到污染，针对单一污染物进行传感是不切实际的，因此必须在不同连接点部署一组传感器并进行协同工作，以便共同覆盖所有主要污染物。在本文中，我们提出了一种协作式自适应采样率自适应方案，该方案基于单个节点的采集能量以及各类水质传感器的相关传感能力。因此，本文的主要贡献如下：

• 我们开发了一种传感器网络架构，其中固定传感器通过人孔部署，并由从流动水中采集的能量供电。

由于管道中的流速有时可能不足以收集到维持传感器网络运行所需的足够能量，我们提出了一种基于节点能量预算的最优采样和传输速率自适应方案。

• 在可以实现自动人工水循环的系统中，我们研究了为保持传感器网络运行所需的最小循环问题。

• 我们利用多个水质传感器的相关传感能力，通过形成传感器联盟来有效感知多类污染物。

我们通过使用现有测量数据进行广泛的仿真研究，量化了该方法的优势，并表明所提出的方法在仅需极小的人工循环时，可在深夜时段将报告时间从3.5小时减少至∼6min。

据我们所知，这是首个在供水系统实际约束条件下尝试实现供水管网最优监测的研究工作。

与任何信息物理系统一样，安全问题在水质监测网络中也变得至关重要，但对安全问题的全面探讨已超出本文的范围。在大多数情况下，水质监测网络的安全面临相似的挑战，并可采用与其他无线传感器网络相同的方法（例如，参见参考文献[8, 9]）。我们为关键智能电网通信开发了一种轻量级完整性机制，该机制也可用于水质监测网络[10]。

文章的结构如下。第2节概述了供水系统，并讨论了泄漏与污染检测问题的动机。第 3节描述了水质监测网络和人工水循环机制。第4节提出了WDSN充电模型，以在低水流时段为传感器网络提供充足的能量。第5和6节基于节点能量预算研究传感速率自适应问题。第7节给出了方案评估。相关工作在第8节中报告。文章在第9节进行总结。

2 背景

2.1 水泄漏与污染问题

城市供水系统中的泄漏问题在全球范围内普遍存在，甚至在最发达的国家也十分严重。例如，在美国，大多数水務系統已有 100+年历史，尤其是在东海岸的大城市。例如，2010年费城的一项审计显示，由于泄漏导致的水资源损失达26%，另有8%是由于计量不准确、窃水以及数据处理与管理问题所致[12]。参考文献中的综合调查显示，美国36个城市的损失百分比介于15%至35%之间，如表 1 所总结。欧洲因泄漏损失超过25%的水，一些国家甚至达到50%[13]。

美国环保署报告[14]全面分析了美国饮用水配送系统中的水资源损失情况，包括水量计量、水表类型、水平衡审计、泄漏检测与定位、管道更换/修复以及维护与预防措施等方面的详细信息。费城水务局昆克尔[15]及其早前著作[16]对水务系统的现状以及泄漏监测与修复进行了全面讨论。参考文献[17]详细综述了水管实用的漏损管理方法。

由于通过泄漏点、生锈管道、内部积聚、操作失误等导致的渗漏，污染与泄漏问题密切相关。水源性疾病暴发事件频发。在加拿大沃克顿，由于资源污染，大肠杆菌污染饮用水，导致2500人中毒，7人死亡，该事件发生在 2000[18]年。2007年，芬兰诺基亚因废水与配水网络发生交叉连接，导致8500人患病。

由于潜在污染物或化学物质种类繁多，针对每种特定化学物质进行传感检测可能非常昂贵且缓慢，因为通常需要采集水样，加入合适的试剂进行处理，测量特定的副产物，然后将水样丢弃。这一难题促使人们采用代理感知技术，通过易于测量的水质特性（如pH值、电导率、温度或添加氯的耗损曲线）来推断某些化学物质的存在。

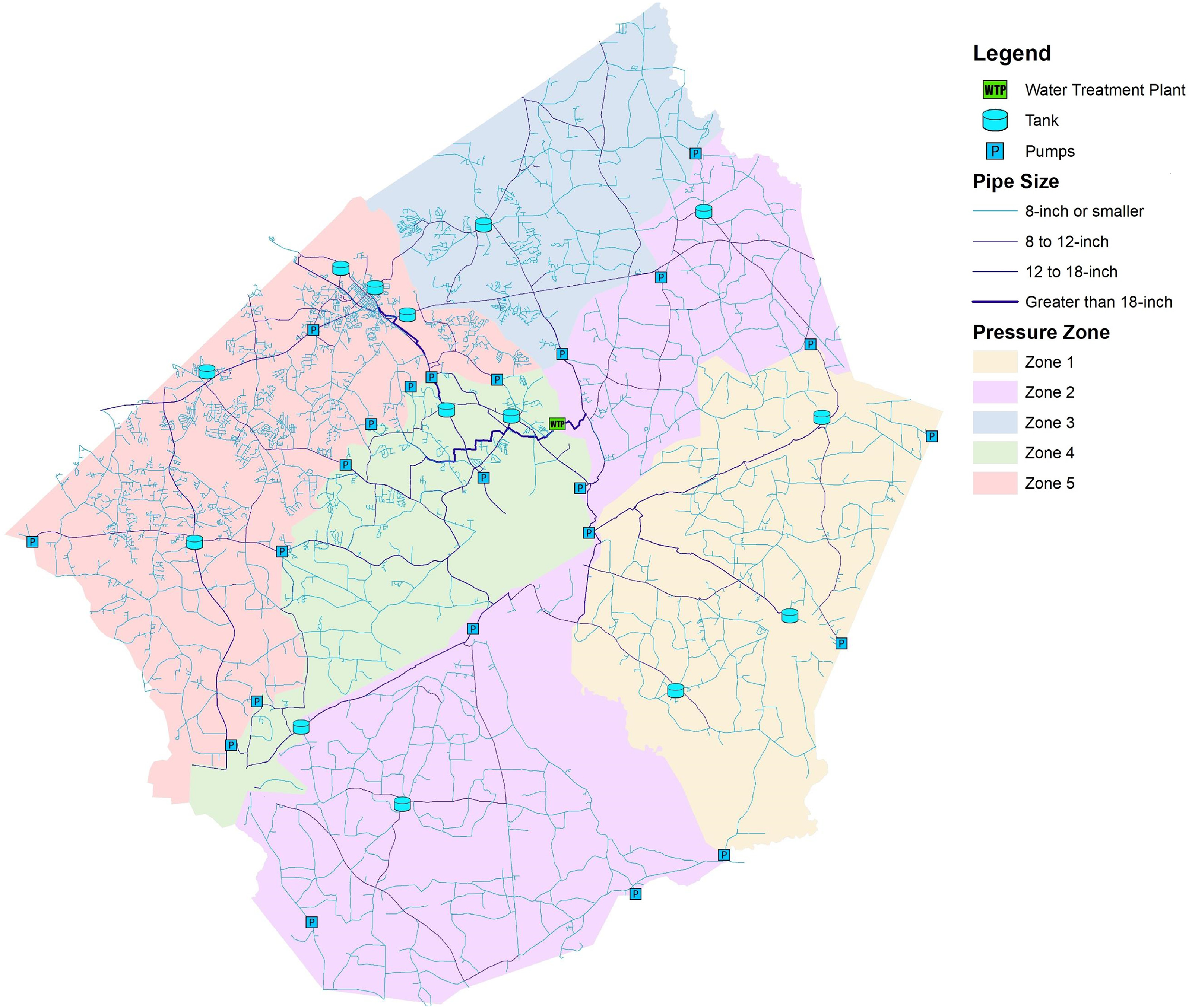
2.2 配水管网

一个配水系统由多个水库和从其延伸出的主管道组成，进一步划分为支干管和分支管道，并从这些管道引出服务连接供给用户。该网络包含多个泵站，可根据需要产生水流，以满足用水需求以及向水箱储水。如今，该网络越来越多地配备先进的监控与数据采集系统，可通过控制室进行访问，从而实现对水泵的远程操作以及对抽水量的远程控制[19]。我们将利用这一能力，生成一种偶尔的人工水循环，以保持所提出的传感器网络运行。

图1显示了一个供水管网的示例。整个网络相当不规则，密集连接区域服务于人口更密集的地区，布局紧密跟随道路布局。颜色代表不同的水压区，其中一区为最低，五区为最高。该图为循环结构，但水流受阀门设置的影响——某些阀门可能只允许单向流。然而，水流回路确实存在且属于正常现象。节点度普遍较小，很少超过4。管道和连接部分由于其使用年限、工艺、运行环境以及所用材料的不同，可能处于各种不同的物理状况，包括沉积物、锈蚀/腐蚀、裂缝/孔洞、薄弱部位、劣质/泄漏接头，以及

供水管网通常被划分为分区计量区域或DMAs。一个DMA通常覆盖一个街区，仅有少量进出主管道，可被视为一个子网，效用公司希望能够将其隔离或调控。因此，所有从 DMA进出的管道都安装有阀门和流量/压力计。至少应在DMA的粒度上安装传感/通信设备，但更密集的部署可能非常理想。

2.3 水泄漏与污染的传感

人们已开发出多种传感技术用于水利基础设施的监测，这些技术涵盖磁学、声学、超声波、热感、视频成像等多种类型。根据型号的不同，传感器可安装在水管附近区域、管壁表面，或插入管道内部。参考文献中的美国环保署报告[14]对各类传感器进行了详细讨论。超声波技术利用施加的超声信号的波传播时间差（多普勒频移）测量流体速度。电磁感应产生的电压与流速成正比，在较宽范围的流量下均具有较高的准确性。这两种设备均可测量水流速率，但在存在大量压力瞬变的噪声环境中将其与微小泄漏关联起来可能极具挑战性。

声学方法通常通过检测泄漏的水产生的振动来实现直接泄漏检测，以确定泄漏的位置和程度[20]。振动频率通常随着泄漏尺寸的增大而降低；因此，该方法对较小的泄漏更为有效。然而，较小的泄漏产生的音量也更低。市场上现有的一种方法（撒哈拉泄漏检测）将有线声学装置插入管道中进行泄漏检测，并已被用于检测水管泄漏。声学设备的有效性因多种因素而异，例如泄漏类型、开口大小、管材和土壤条件[21]。在某些情况下，使用声学设备可能无法检测到泄漏，例如存在背景泄漏时、泄漏引起的压力非常低时，或探测时土壤已经饱和含水。地震检波器可用于检测/监测地表声音。但总体而言，这些方法充其量较为粗糙，且需要操作员具备较高的专业知识/培训水平。许多其他技术已被提出，但都存在这样或那样的问题。化学示踪剂在确定泄漏量或泄漏位置方面并不十分准确。探地雷达（GPR）可以准确地检测和定位泄漏[22–24]但需要大量人工参与以及完整的分配系统地图。基于泄漏导致固体特性变化的方法可能有用，但准确性不高。通过人为制造压力瞬变（例如通过开关阀门）可用于漏损检测与定位[25]但需要繁琐的校准，且无法适用于长管道，因为瞬变过程会在长距离上传播衰减。利用管道内检测机器人进行泄漏检测的方法见参考文献[26, 27]。

许多水质传感器通常用于监测常规的水质参数，例如pH值、氯、总有机碳（TOC）、氧化还原电位（ORP）以及电导率和温度[28, 29]。一些研究致力于利用这些传感器获取的数据进行污染事件检测。在参考文献[30]中，作者研究了不同污染物对现成商用产品在监测标准饮用水参数（如pH值、游离氯、氧化还原电位（ORP）、溶解氧、比电导、浊度、总有机碳（TOC）、氯化物、氨和硝酸盐）方面的响应。大多数传感器对大量测试污染物均有响应。在参考文献[31]中，作者探索了一种使用11种化学和生物污染物的实时事件自适应检测、识别和预警（READiw）系统。在参考文献[32]中，作者已

研究了来自五种独立水质测量（pH值、电导率、浊度、余氯、TOC）的信号以触发污染事件。在参考文献[33]中，作者提出了一种基于Dempster‐Shafer证据理论的饮用水系统污染检测方法。数据驱动估计模型用于水质污染检测在参考文献[34, 35]中已有报告。

如前所述，在地下管网基础设施中部署合适的传感与通信系统极具挑战性，这使得许多方案难以实施。例如，许多解决方案提出了在管壁表面进行传感器密集部署，包括 PipeNet[36], NAWMS[37], MISE-PIPE[38],和PipeTECT[39],但这种方法不太现实。其他提议如SPAMMS[40]需要在管道内壁涂覆RFID标签，同样不切实际。像Kadri中提出的流动式声学传感器这样的流动传感器更为现实，但需要精心规划手动插入和从管道中取出，且可能卡在管道内部（例如被藻类缠住）或阀门周围。像TriopusNet这样的自主移动式机器人流动传感器可能更灵活，但更适合特殊检测任务，而非日常使用。关于固定传感器的其他提议包括[43–46]也存在类似的限制。

与这些方法不同，我们的研究重点是仅涉及在可进行传感的连接点处监测水流特性和污染的技术。通信方面存在一定的挑战，因为将天线部署在井盖外部的唯一实用方法是将其集成在智能井盖顶部（例如，坚固且平躺在井盖顶部的环形或偶极子天线，以便车辆碾压不会影响其工作）。泄漏检测仍然具有挑战性，因为泄漏很可能发生在管道中间某处，而在连接点处可测量的参数仅有流速、压力以及可能的流型。对于较大的泄漏，可以通过历史记录的流速和压力数据，并比较随时间的变化，来确定泄漏可能发生的位置，精确到管道段落。更精确的定位可以通过使用WaterGEMS等软件包对网络进行协同仿真来实现。

然而，本文并不侧重于详细探讨此类方法；本文的重点在于保持传感网络的正常运行并高效工作，以充分发挥已部署传感器的能力。

3 水流驱动的水质监测网络（WDSN）

我们假设一种基于软件的泄漏/污染检测方案，其中整个DMA在模拟器（如 Water‐GEMS）中建模[47]。布置在DMA不同位置的传感器节点记录并报告污染监测参数以及压力、温度、流速等数据。这些传感器读数随后与相应位置的模拟值进行比较。如果某个节点的传感器数据与模拟器的输出存在显著差异，则怀疑该传感器节点附近区域存在泄漏或污染。因此，通过部署的传感器持续监测DMA系统的水力学状态，可以实时发现可能表明泄漏的异常情况（例如压力或流量需求的显著变化），如图2(a)所示。一旦怀疑发生泄漏/污染，可采用传统直接人工检查方法[48, 49]来精确定位泄漏位置或污染源。

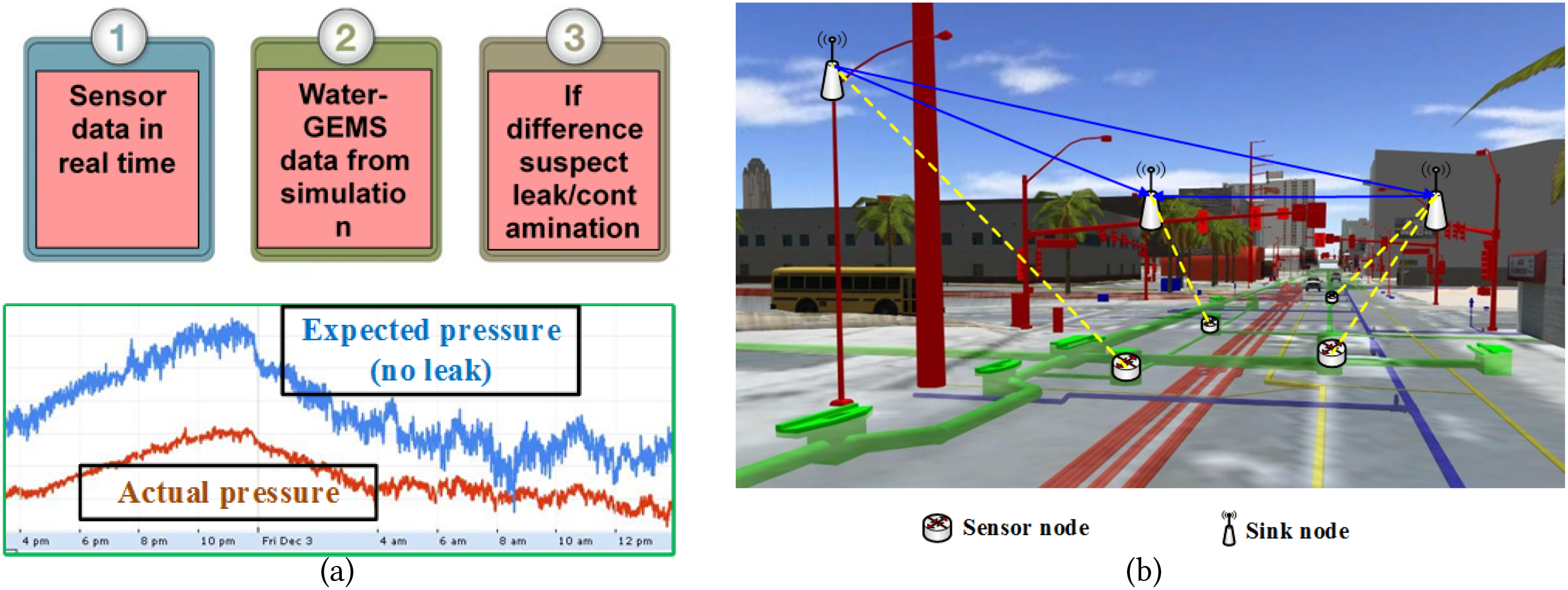供水系统水质监测网络中的间接泄漏/污染检测。(b) 所提出的供水系统水质监测网络的架构。)

3.1 网络操作

如前所述，我们假设传感和通信节点仅部署在连接点处，并从流动水中获取能量。我们假设这些节点不是时间

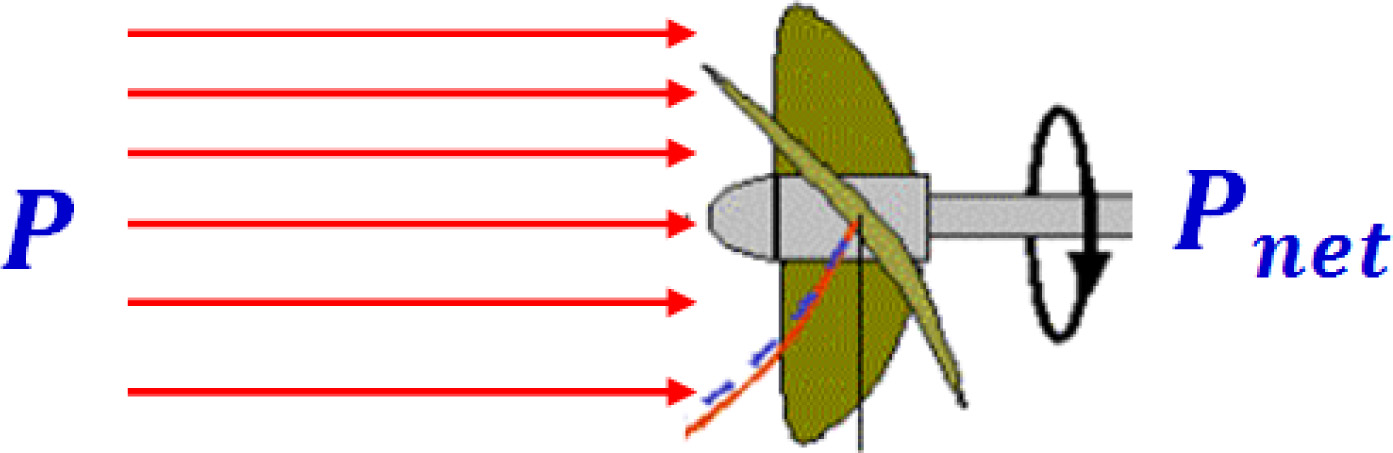一种基于风扇的能量收集器。(b)Pnet在不同水流速度下的表现。)

同步并使用基本的低功耗监听（LPL）[50]原理来节省能量。1在LPL中，空闲接收器以适当的睡眠/唤醒占空比运行，发送方总是在其消息前添加足够长的前导码，以确保与处于睡眠状态的接收器进行通信。此外，我们还假设部署了一组战略位置的汇聚节点用于数据采集。这些汇聚节点被认为具有稳定的电源（例如交流电或长效电池），并且具有到DMA中中央控制节点的第二通信接口（可能是有线的）。我们假设汇聚节点的部署不受人孔位置限制，而是基于可访问性和供电可用性的考虑。所有非汇聚节点通过单跳直连WiFi/远距离Zigbee通信收集、存储并将传感数据和剩余能量转发至最近的汇聚节点。虽然通常可以通过基于树的转发机制实现多跳通信[51–53],但本文仅限于单跳通信。单跳限制可能需要在分区计量区域内部署多个汇聚节点，这些节点能量充足且始终处于活动状态。它们可以通过长距离WiFi/3G/4G/LTE技术相互之间以及与控制中心进行通信。尽管并非必需，为简化起见，我们假设其中一个汇聚节点是特殊的，所有其他节点都将数据发送给它，由其最终传送到控制中心。整个水质监测网络架构如图2（b）所示。

水质监测网络中的普通传感器节点所采集的能量取决于水流速率。我们假设每个节点都配备了一个合适的基于风扇的能量采集器，流动液体的动能带动叶片旋转并产生电能，如图3(a)所示。这种能量转换的基本方程已被充分研究确立[54]。流速为v(m/s)的流体通过面积为A(m 2)的风扇时，其动能功率（单位：瓦特）由以下公式给出

P= ∂ mv2)= 1 2 v2 ∂m ∂t = 1 2 v2ρAv= 1 2 ρAv3, (1) 其中m为流体质量， ρ为密度（水的密度为1,000 kg/m3）。设η f d表示旋转体的流体动力效率， ηem为机电转换效率，ηsc为超级电容器的充电效率。则用于超级电容器充电的净电功率为

Pnet= η f d η em η sc = η e · P, (2) 其中 η e表示整体效率。不用说， η e取决于多种因素，属于机械/电气设计领域。这里我们仅假设 η e —˜通常不会优于10%。图3（b）显示了最终收获的功率Pnet作为

使用2.5英寸直径风扇时的水流速率与 ηe= 5–15%。该图最引人注目的方面是，在极低水流速度下，采集能量实际上为零，因此需要有效管理以确保在低流速期间（尤其是夜间水流速率可能持续数小时偏低时）的正常运行。

3.2 保持网络存活

保持水质监测网络（WDSN）持续运行的最简单方法是选择容量足够的超级电容器以度过长期的低谷期。然而，这种方法不仅使解决方案变得非常昂贵，而且忽略了一个供水管网的重要方面：如果流速非常低，则泄漏率和污染扩散速率也会非常低。因此，更好的思路是适应充电速率来调整采样和传输速率，从而在无需大量能量存储的情况下提供有效的覆盖范围。事实上，这里存在一种内在的补偿机制：如果在低谷期发生大泄漏，相关传感器将自动充电并恢复正常运行。类似地，一个泄漏严重的系统可能始终提供充足的可收集能量，此时使用大电容器则是浪费的。然而，在长时间的低谷期内让污染监测频率大幅下降可能是不可取的。为此，我们提出在分区计量区域（DMA）内采用人工水循环机制来补充超级电容器。

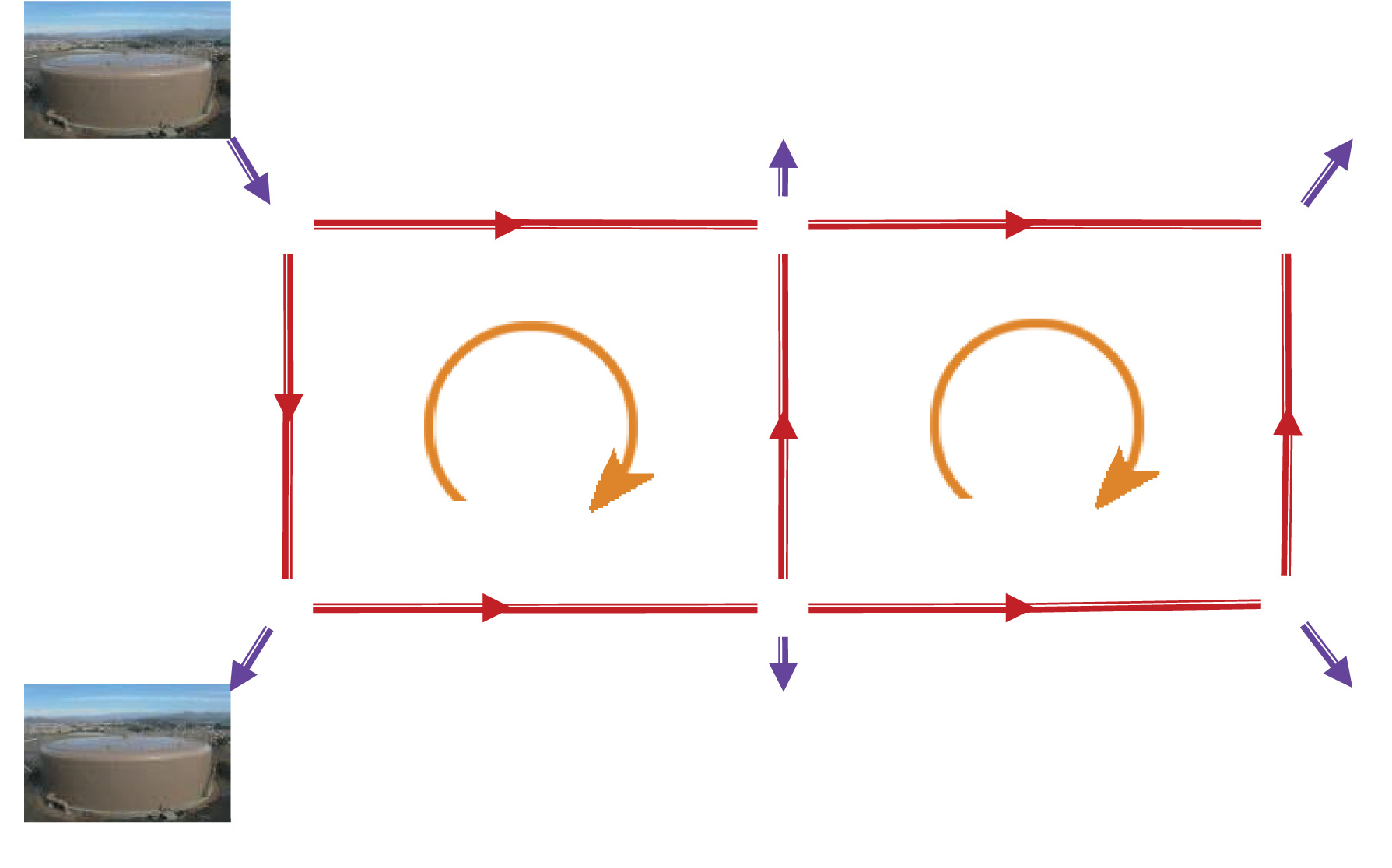
我们利用此能力进行人工循环水，以产生水流。这种水循环不会造成任何水资源损失——它只是水库之间的环形流动，如图 4 所示。此处从节点1和2注入或抽出系统中的水，也会在其他附近环路中产生额外的水流，如图所示。显然，孤立循环的影响会随着远离循环区域而迅速减弱。换句话说，如果希望在距离水库和水泵多跳的管段中产生较大的人工水流（例如图 4 中的5‐6段），则需要较大的人工流速，而这可能无法实现或不理想。在这种情况下，我们可以采用另一种技巧——在某些点进行人工排水（例如，在节点5或6）。这种可从控制室操作的能力在水務系统中正变得越来越普遍，主要用于冲洗管道。出于明显的原因，我们希望尽量减少此类人工 泄漏。即使没有自动控制，如果手动操作非常不频繁，人工循环和泄漏机制也可能有用。

显然，超级电容器的容量（以及相应的成本/尺寸）与所产生的人工流动的频率和幅度之间存在一种权衡。较大的超级电容器可以在夜间通过1‐2次显著流动完成充电，而较小的则需要多次较小的水流。它是一种

可以根据所有这些因素定义一个确定超级电容器尺寸设计的优化问题，但由于篇幅限制，我们不深入讨论该问题。相反，我们讨论一种用于计算在不同连接点所需流速的模型，以提供足够的采集能量供所有传感器节点使用。这一方面自然与基本的速率自适应机制相关联，而该机制是减少循环需求所必需的。

4 水质监测网络人工水循环模型

我们假设，每当一定数量的传感器节点的电压降至阈值充电时间 τ以下时，分区计量区域（DMA）中的所有传感器节点都会进行短暂的充电。设电压ini和电压target分别表示超级电容器的初始电压和所需目标电压， C为超级电容器的电容。则通过充电在超级电容器中存储的能量为[55]

Pnet.τ ≥ 1 2 C(V2 target − V2 ini), (3)

其中Pnet是公式（2）中的充电功率。因此，所需的水流速度由下式给出

v ≥[C(V2 target − V2 ini)/τ · ρ · A · ηe] 1 3 = V(assume). (4)

因此，充电后所有节点的电压至少为Vtarget。（注意，那些几乎已充满电的节点可能不会接受太多额外电荷。）用于充电的人工水流只能在加压点P P 处产生，这些加压点是与水库/水箱相关联的水泵。从P Ps处可以以一定的调节速率向系统内泵入或抽出水。实际上，加压点能产生的水流速或管道可承受的水流速均存在最大限值。接下来我们描述三个基于不同设计目标的优化问题。

MIN_DIFF：由于加压点的数量有限，且其泵送速率也受限，因此可能无法满足所有传感器节点的最小流速要求（公式(4)）。因此，MIN_DIFF的目标是最小化在放置传感器节点的所有管段上，所需流速与实际达到的流速之间差异的总和。设ai、Qj、Rj分别表示节点i的节点流量、管道j的管道流量和管道阻力。设v i和Ai分别表示第i条管道的水流速度和截面积，Vj表示管道j处传感器节点所需的最小流速。设 V max j 表示管段j所能支持的最大水流速度，amax i 表示加压点i所能支持的最大流量。C和L

分别表示分配系统中连接点和环路的数量，P 表示所有管道的集合，S 表示放置传感器节点的子集。然后，

Minimize ∑ j ∈S max(0, Vj − vj) subject to vj= |Qj | Aj ≤ V max j , ∀j ∈ P ± ai ± ∑ pipe j connected to i Qj= 0, ∀i= 1, 2,…, C ± ∑ pipe j ∈ Ll Rj Q 2 j= 0, ∀Ll= L1, L2,…, LL |ai| ≤ amax i ∀i ∈ PP. (5)

我们已在公式(5)中使用达西‐魏斯巴赫公式来计算摩擦水头损失。在非加压点中，如果某个连接点i处存在背景流量，则将ai赋值给该背景流量。否则，在非加压点处假设ai为零。这些背景流量可根据传感器节点报告的水流测量结果进行估算。

在公式(5)中，第一组约束条件确保通过第j段管道的水流速度j（等于该管道段的体积流量/流量除以管道段的横截面积）小于该管道段所能承受的最大水流速度 V max j 。第二组约束条件是节点流量连续性关系node-flow continuity relationships，用于确保所有连接点处的流入和流出总和为零。第三组约束条件是回路水头损失关系loop-head loss relationships，表明形成回路的管道中水头损失的总和为零[56]。在这两个约束中使用 ±符号是为了考虑假设的水流方向。第四个约束条件指出，所有加压点i处的水流速率小于某个最大阈值amax i 。注意，当MIN_DIFF的目标值为零时，加压点能够满足所有传感器节点的流速要求。

MIN_泵水： 如果所有传感器节点的流速要求都能被满足，则我们希望以最小化泵水量的方式实现。注意，只有当MIN_DIFF的结果为目标值为零时，才求解MIN_ PUMPING。鉴于对MIN_DIFF的符号和解释已明确，以下公式表述清晰，不再进一步说明：

Minimize ∑ i∈PP |ai| subject to v j = |Qj | A j ≤ V max j , ∀j ∈ P v k ≥ Vk , ∀k ∈ S ± a i ± ∑ p i p e j connected to i Qj = 0, ∀i= 1, 2,…, C

± ∑ pipe j ∈ Ll Rj Q 2 j= 0, ∀Ll= L1, L2,…, LL |ai| ≤ amax i ∀i ∈ PP. (6)

MIN_流量： 该问题是最小_加压问题的一个变体，我们假设存在一组排放点（或故意泄漏点）LP，在这些点上可以以不同的调节速率故意排放水。由于加压点数量有限，其思路是在充电时间内从某些管段排放/泄漏一定量的水，以产生足够的水流来维持传感器节点的运行。由于排放会造成水的浪费，因此我们希望最小化排放量。该问题可建模如下：

Minimize ∑ i∈LP |ai| subject to vj= |Qj | Aj ≤ V max j , ∀j ∈ P vk ≥ Vk, ∀k ∈ S ± ai ± ∑ pipe j connected to i Qj= 0, ∀i= 1, 2,…, C ± ∑ pipe j ∈ Ll Rj Q 2 j = 0, ∀Ll= L1, L2,…, LL |ai| ≤ amax i ∀i ∈ PP ∪ LP. (7)

在上述公式中，目标值为零意味着在没有任何水流量（浪费）的情况下，加压点仍可满足节点的需求。在这种情况下，通过再次求解与之前相同的MIN_PUMPING问题，可以实现保持加压点最小流速的次要目标。

我们使用图4中的简单示例来说明这些问题。假设水从水库1泵入，从水库2泵出。令节点3–6为排放点，其排放速率为a3–a6。因此，节点流量连续性关系和环路水头损失关系如下所示：

a1 − Q1 − Q2= 0 Q1 − a2 − Q3= 0 Q3 − a3 − Q4 − Q6= 0 Q4+ Q2 − a4 − Q5= 0 Q5+ Q7 − a5= 0 Q6 − a6 − Q7= 0 ⎫⎪⎬⎪⎭ Node-flow continuity relationships, (8)

R2Q 2 2 − R4Q 2 4 − R3Q 2 3 − R1Q 2 1 = 0 R5Q 2 5 − R7Q 2 7 − R6Q 2 6 + R4Q 2 4 = 0 ⎫⎪⎬⎪⎭ Loop-head loss relationships. (9)

方程（8）仅仅是图4中每个节点的流量守恒定律。方程（9）表示任何环路中的环路水头损失必须为零。

我们使用AMPL求解此情况下的上述优化问题，AMPL是一种用于求解大规模优化问题的建模语言[57]。所需参数列于表2中。最大抽水能力a max（表2中假设为0.069m3/s）对应于直径为8英寸的管道中流速为7英尺/秒的情况。

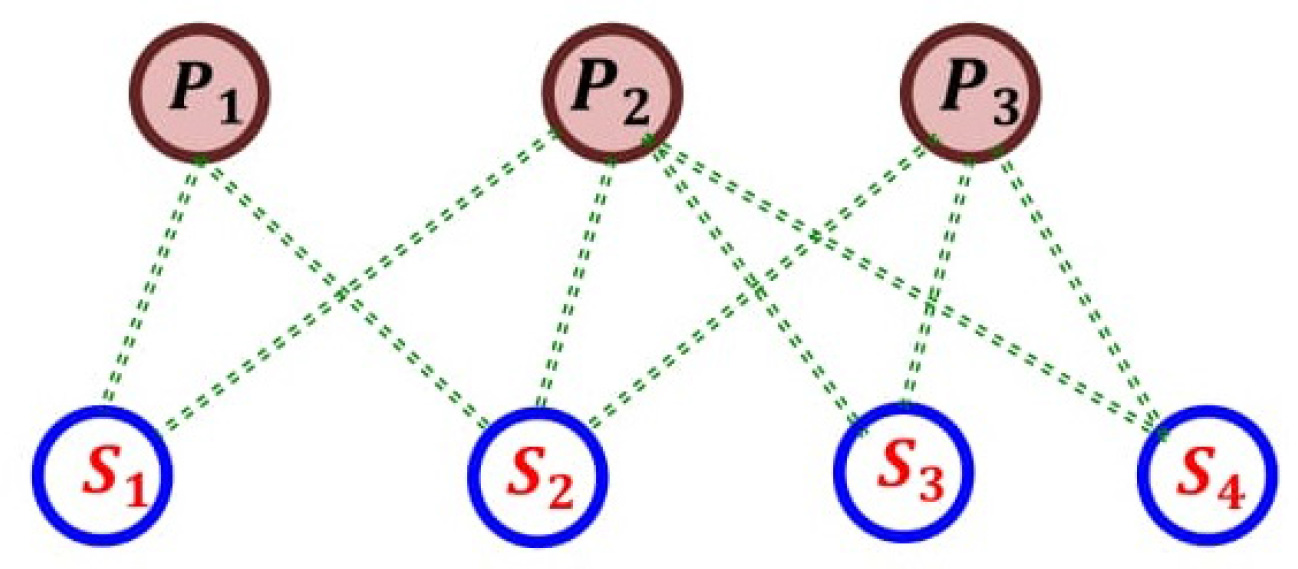
图 5显示了不同∑j ∈P 最大值(0、变量j − v j) 随充电时间的变化情况。正如预期，目标值随着充电时间的增加而减小，并且随着目标的降低而减小

电压 Vtarget。图 6显示了通过 PPs 泵入和泵出的总水量随充电时间的变化情况。在图 6中，最初优化问题 MIN_PUMPING 不可行，因此图中没有数据点。当 MIN_DIFF 的目标值为零时，MIN_PUMPING 开始给出可行解，且该解也是充电时间的递减函数。

图 7显示了在不同充电时间下的总放电量，其中最大放电速率假设与最大泵送速率相同。请注意，图5和7表现出高度相似性，这是因为在MIN_DIFF中，每当所需速度与实际达到速度之间存在非零差异时，MIN_DISCHARGE中就需要有非零的流量。此外，随着充电时间的增加，总放电量减少，因为传感器节点有更多时间为其超级电容器充电。

5 泄漏监测中的采样率自适应

如前所述，根据超级电容器中的当前电荷状态自适应调整测量/传输活动，对于维持泄漏/污染检测活动的最大覆盖范围至关重要。即使在人工水循环条件下也是如此，因为供水管网某些管段中的传感器节点可能难以有效充电。

通常，位于附近区域的一组传感器节点在水流方面可能存在显著的相互依赖性，从而影响其可充电能力以及泄漏/污染检测性能。我们可以将这些节点视为在博弈论意义上形成一个联盟，该联盟可用于提升性能。可通过在不同管道段使用任何商业模拟器（如 Water‐GEMS）模拟泄漏/污染，并结合分析单个节点检测能力之间的相互依赖性来形成联盟，即如果联盟内的任意管道段发生泄漏/污染，至少有若干传感器节点能够检测到该事件。联盟成员可根据各节点的能量可用性协作调整其采样率，例如，能量收集较少的传感 器节点的低采样率可由能量较多的节点的高采样率进行补偿。这种机制与文献中讨论的基于单个节点的速率/能量分配方案截然不同[47]，相关内容将在下文讨论。[58, 59]并且在下文中讨论。

我们假设时间被划分为 区间，每个区间为T个时间单位。采样率在每个区间周期性地更新，具体如下：所有节点记录其在每个区间内的平均采集能量。基于它们的历史能量分布，节点预测下一区间的预期采集能量，然后传感器节点利用该预测值计算其最大可能采样率，如第5.2节所述，该采样率用于压力或水流传感器。与泄漏检测传感器（如压力或水流传感器）不同，潜在污染物种类繁多，如前所述。在这种情况下，传感设备配备有异构且多种的传感器。此类异构多传感器设备的协作自适应方法在第 6节中讨论。最大可能采样率通过 beacon消息进行广播。汇聚节点利用这些速率计算各个节点的最优采样率，并通过发送信标消息进行广播，如第5.2节所述。

5.1 预测能量收集

图 8展示了能量采集的概念模型。可用能量存储在能量队列（EQ）中，本例中为超级电容器。采样的值存储在易失性内存中，我们称之为数据队列（DQ）。在发送数据包时，传感器节点从RAM中取出 个项，其大小为 min ≤ ≤ max。其中， min是节点在具备足够能量进行立即传输前需累积的最小样本数。

然而，如果节点能量不足，则会继续采样并将样本存储在随机存取存储器中（如果可能的话）。当下一个能量脉冲到达时，它将传输所有累积的样本，最多达到 max的限制。

每个传感器节点使用归一化最小均方自适应滤波器，在周期为T的区间内估算其超级电容器中的能量到达。在NLMS滤波器中，历史能量采集曲线存储于向量Et−1中。基于该曲线，通过Et−1与自适应滤波器系数Wt−1的点积，计算下一区间 λ t的预测采集能量，即 λ t= Et−1Wt−1，并记录误差et。随后，滤波器系数将被更新。

Wt= Wt−1+ s · et · Et−1 1+ |Et−1|2, (10) 其中s是滤波器的步长。假设超级电容器泄漏功率以及由于不同操作（传感/传输/接收等）导致的平均功耗分别为 μl和 μe。平均功耗 μe需要根据能量可用性进行调整，以维持节能，即 Ae+ λ t −(μe+ μl)T ≥ 0 ∴ μe ≤ Ae+ λ t T − μl, (11) 其中Ae是该区间t开始时的可用能量。

采样值以到达率r存储在DQ中，而数据包传输速率为μp。注意， λ t和 μe以能量为单位表示，而r以采样数量为单位表示。我们计算传感器节点在下一个时间区间内能够支持的最大采样率，且不发生DQ缓冲区溢出。假设在计算最大采样率时，DQ中等待的包数量为 N。 DQ的容量假设为C。为了维持能量预算， μe= A ·r+ B · μp+ C，其中 A、 B和 C分别为表示传感、传输及其他操作（信标发送/接收、处理等）功耗的常数。为了避免DQ缓冲区溢出， N+(r − m · μp) · T ≤ C ∴ r ≤ C−N T + m · μp = C−N T + m μe − A · r − C B ∴ r ≤ C−N T + m μ e −C B 1+ m · AB = R(assume), (12) 这给出了采样率的上限。所有传感器节点周期性地计算其最大采样率R，并在信标消息中广播，汇聚节点利用该信息来确定各个传感器节点的采样率。

5.2 计算最优采样率

在接收到来自所有传感器节点的最大采样率R后，汇聚节点制定采样率自适应问题，在满足所需能量约束的前提下最大化某个效用函数。假设一个联盟中有N个节点。由于联盟中传感器节点的检测能力高度相关，联盟中的传感器节点可根据其可用的收集能量共享数据采样任务，以降低能耗。我们通过考虑两个因素来定义节点i的效用

• 传感速率ri。随着ri的增加，采样点的数量增加，效用也随之增加。

在
电压 Vtarget。图 6显示了通过 PPs 泵入和泵出的总水量随充电时间的变化情况。在图 6中，最初优化问题 MIN_PUMPING 不可行，因此图中没有数据点。当 MIN_DIFF 的目标值为零时，MIN_PUMPING 开始给出可行解，且该解也是充电时间的递减函数。

图 7显示了在不同充电时间下的总放电量，其中最大放电速率假设与最大泵送速率相同。请注意，图5和7表现出高度相似性，这是因为在MIN_DIFF中，每当所需速度与实际达到速度之间存在非零差异时，MIN_DISCHARGE中就需要有非零的流量。此外，随着充电时间的增加，总放电量减少，因为传感器节点有更多时间为其超级电容器充电。

5 泄漏监测中的采样率自适应

如前所述，根据超级电容器中的当前电荷状态自适应调整测量/传输活动，对于维持泄漏/污染检测活动的最大覆盖范围至关重要。即使在人工水循环条件下也是如此，因为供水管网某些管段中的传感器节点可能难以有效充电。

通常，位于附近区域的一组传感器节点在水流方面可能存在显著的相互依赖性，从而影响其可充电能力以及泄漏/污染检测性能。我们可以将这些节点视为在博弈论意义上形成一个联盟，该联盟可用于提升性能。可通过在不同管道段使用任何商业模拟器（如 Water‐GEMS）模拟泄漏/污染，并结合分析单个节点检测能力之间的相互依赖性来形成联盟，即如果联盟内的任意管道段发生泄漏/污染，至少有若干传感器节点能够检测到该事件。联盟成员可根据各节点的能量可用性协作调整其采样率，例如，能量收集较少的传感 器节点的低采样率可由能量较多的节点的高采样率进行补偿。这种机制与文献中讨论的基于单个节点的速率/能量分配方案截然不同[47]，相关内容将在下文讨论。[58, 59]并且在下文中讨论。

我们假设时间被划分为 区间，每个区间为T个时间单位。采样率在每个区间周期性地更新，具体如下：所有节点记录其在每个区间内的平均采集能量。基于它们的历史能量分布，节点预测下一区间的预期采集能量，然后传感器节点利用该预测值计算其最大可能采样率，如第5.2节所述，该采样率用于压力或水流传感器。与泄漏检测传感器（如压力或水流传感器）不同，潜在污染物种类繁多，如前所述。在这种情况下，传感设备配备有异构且多种的传感器。此类异构多传感器设备的协作自适应方法在第 6节中讨论。最大可能采样率通过 beacon消息进行广播。汇聚节点利用这些速率计算各个节点的最优采样率，并通过发送信标消息进行广播，如第5.2节所述。

5.1 预测能量收集

图 8展示了能量采集的概念模型。可用能量存储在能量队列（EQ）中，本例中为超级电容器。采样的值存储在易失性内存中，我们称之为数据队列（DQ）。在发送数据包时，传感器节点从RAM中取出 个项，其大小为 min ≤ ≤ max。其中， min是节点在具备足够能量进行立即传输前需累积的最小样本数。

然而，如果节点能量不足，则会继续采样并将样本存储在随机存取存储器中（如果可能的话）。当下一个能量脉冲到达时，它将传输所有累积的样本，最多达到 max的限制。

每个传感器节点使用归一化最小均方自适应滤波器，在周期为T的区间内估算其超级电容器中的能量到达。在NLMS滤波器中，历史能量采集曲线存储于向量Et−1中。基于该曲线，通过Et−1与自适应滤波器系数Wt−1的点积，计算下一区间 λ t的预测采集能量，即 λ t= Et−1Wt−1，并记录误差et。随后，滤波器系数将被更新。

Wt= Wt−1+ s · et · Et−1 1+ |Et−1|2, (10) 其中s是滤波器的步长。假设超级电容器泄漏功率以及由于不同操作（传感/传输/接收等）导致的平均功耗分别为 μl和 μe。平均功耗 μe需要根据能量可用性进行调整，以维持节能，即 Ae+ λ t −(μe+ μl)T ≥ 0 ∴ μe ≤ Ae+ λ t T − μl, (11) 其中Ae是该区间t开始时的可用能量。

采样值以到达率r存储在DQ中，而数据包传输速率为μp。注意， λ t和 μe以能量为单位表示，而r以采样数量为单位表示。我们计算传感器节点在下一个时间区间内能够支持的最大采样率，且不发生DQ缓冲区溢出。假设在计算最大采样率时，DQ中等待的包数量为 N。 DQ的容量假设为C。为了维持能量预算， μe= A ·r+ B · μp+ C，其中 A、 B和 C分别为表示传感、传输及其他操作（信标发送/接收、处理等）功耗的常数。为了避免DQ缓冲区溢出， N+(r − m · μp) · T ≤ C ∴ r ≤ C−N T + m · μp = C−N T + m μe − A · r − C B ∴ r ≤ C−N T + m μ e −C B 1+ m · AB = R(assume), (12) 这给出了采样率的上限。所有传感器节点周期性地计算其最大采样率R，并在信标消息中广播，汇聚节点利用该信息来确定各个传感器节点的采样率。

5.2 计算最优采样率

在接收到来自所有传感器节点的最大采样率R后，汇聚节点制定采样率自适应问题，在满足所需能量约束的前提下最大化某个效用函数。假设一个联盟中有N个节点。由于联盟中传感器节点的检测能力高度相关，联盟中的传感器节点可根据其可用的收集能量共享数据采样任务，以降低能耗。我们通过考虑两个因素来定义节点i的效用

• 传感速率ri。随着ri的增加，采样点的数量增加，效用也随之增加。

在水质监测网络中，主干管通常比分支管线更重要，因为主干管中的水会被分配到不同的支干管和分支管线中。因此，安装在主干管中的传感器节点被认为比安装在分支管线中的传感器更重要。于是，我们根据节点i在水质监测网络中的位置，为其采样数据赋予一个相对权重α i i。

除了分布层次结构之外，供水系统人员在确定权重α i时可能还需考虑其他因素。例如，分区计量区域（DMA）内的水压通常存在显著差异，高压区域的节点可被赋予更高的权重，因为这些区域发生泄漏时会导致更大的水资源损失和潜在损害。对于污染监测，可以为靠近水库的节点分配更高的权重，因为任何接近水库的污染都需要尽早检测，以防止其扩散。此外，老旧且易损管道也可被赋予更高的权重。在联盟中，某些传感器节点的检测能力可能高于其他节点，因此这些节点也可被分配更高的权重。

考虑到这些因素，联盟内的加权比例公平性可以通过将节点i的效用函数建模为Ui(ri) = α i · log(ri)来实现，其中 α i是归一化权重。我们的目标是在满足单个节点的能量预算的前提下，最大化联盟的总体效用，即∑N i=1 Ui(ri)。我们还假设汇聚节点对一个联盟设定每时间间隔最多M 样本/时间间隔的上限，以避免冗余采样，即∑N i=1 ri ·T ≤M，或∑N i=1r i ≤ M T = M。直观上，我们可以认为联盟中的传感器节点共同作为一个单一的虚拟传感器节点，以最大M 样本/时间间隔的速率进行感知和报告。M基本上是一个控制参数，用于控制联盟的整体采样率，即如果汇聚节点希望更频繁地接收样本，则增加M，反之亦然。因此，该优化问题可表示为 Maximize N ∑ i=1 Ui(ri), subject to N ∑ i=1 ri ≤ M, ri ≤ Ri,∀i, ri ≥ 0,∀i, (13) 其中ri ≤Ri为从公式(12)获得的最大采样率约束(MSRC)。由于对数函数是凹函数，该问题是一个凸优化问题，可通过求解相应的拉格朗日函数和卡鲁什‐库恩‐塔克(KKT)条件进行集中求解。我们提出了一种求解该问题的算法，将在第5.3节中介绍。

5.3 提出的自适应速率分配方案CARA

基于上述步骤，我们现在描述所提出的协作式自适应速率分配（CARA）方案，如算法1所示。 在该算法中，汇聚节点维护两组节点：未分配集合U和已分配集合A。初始时，所有节点都属于集合U，但随着为其分配采样率，这些节点将被转移到集合A。汇聚节点首先为每个传感器i分配采样率ri = α i ∑ i ∈ U α i M（第4–7行）。已分配采样率ri与最大采样率Ri之间的差值存储在diff[i]中。在此采样率分配之后，若任意节点j违反了最大采样率约束（MSRC，由公式（12）得出），则计算diff[j]< 0。对于这些节点，汇聚节点将其采样率设置为其最大采样率Rj（第11行），并将diff[j]公平地分配给其他节点（第14–17行）。此过程持续进行，直到所有节点均满足最大采样率约束为止。最终计算出的采样率被广播至所有传感器节点。

; 16: diff[i]= Ri − ri 17:结束循环 18: diff[j]= 0 19: else 20: EXIT 21:结束如果 22:结束循环 23：返回ri ∀i)

所提出方案的最优性：所提出的方案根据节点的加权效用并考虑能量约束，公平地为所有节点分配采样率。我们证明了在给定假设下，所提出的方案是最优的。我们首先提出并证明以下引理1和引理2。

引理 5.1。 优化问题的解 Maximize N ∑ i=1 Ui(ri)= N ∑ i=1 α i · log(ri) subject to N ∑ i=1 ri ≤ M, ri ≥ 0,∀i (14) 是ri= α i ∑ i α i M， ∀ i={1, 2,…， N}。

证明. 显然ri对于任意 i都不可能为零。这是因为令 ri= 0会导致目标值 −∞。因此，最后一个约束是无效的。于是，问题方程(14)的拉格朗日函数和KKT条件为 L= N ∑ i=1 α i · loд(ri) − λ N ∑ i=1 ri − M , (15) ∂L ∂ri = α i ri − λ= 0, (16) λ N ∑ i=1 r i − M = 0. (17) 公式（16）给出r i = α i λ 和 λ 0。代入公式（17），得到 λ= ∑ i α i M，从而得出r i = α i ∑ i α i M。

引理 5.2。 如果一个节点的采样率从问题公式（14）中的最优速率降低了 δ，并将该降低量按比例分配给其他节点，则总体目标函数是关于 δ的递减函数。

证明。假设对于任意节点j，我们分配一个数量 αj ∑i α iM −δ并按比例将其 δ分配给所有其他节点，使得所有节点i j被分配的速率为 α i ∑i α i M+ α i ∑ij α i δ。假设Δ=∑N i=1 α i且 Γ=∑ij α i。如果新的目标函数为F(·)，则我们可以证明 F= αj log(αj Γ M−δ)+∑ ij α ilog(α i Γ M+ α i Δ δ), ∂F ∂δ = − αj αj Γ M−δ +∑ ij α i Δ(MΓ+ δ Δ) < 0. (18) 因此，F(·) 是 δ 的严格递减函数。

理论 m 5.3.所提出的CARA算法为问题方程（13）提供了最优解 .

证明. 由引理1可得，对于优化问题方程(14)，有ri= α i ΓM。现在，我们在问题方程(14)中引入最大采样率约束(MSRC)ri ≤，假设rj= α j α j Γ M。 我们分两步考虑这个问题。第一步，我们将总采样率进行划分 ˜ M=Γ αj Rj超过 N个节点。然后利用引理 1，rj= αj Γ · Γ αj Rj= Rj。因此，节点 j的 MSRC被满足。对于任何其他节点 i，ri= α i Γ · Γ α j · Ri= α i α j Rj。此时，通过改变 j的效用无法 进一步提高 rj（减小rj会导致整体目标函数下降，如引理 2所示）。 现在，我们介绍M− ˜ 所有M − M中公平地分配给i j。根据引理1，所有i j的新采样率为 rnew i = ri+ α i Δ ·(M− M˜)= α i αj Rj+ α i Δ · M− α i Δ · Γ αj · Rj = α i Γ · M+ α i Δ(αj Γ · M− Rj)= ri+ α i ∑ ij α i · abs(diff[j]), (19) 这与根据算法1（第15行）分配的速率相同。在此阶段，如果其他任何节点违反MSRC约束，则执行类似操作，直到所有节点都满足MSRC约束。因此，获得了所有节点的最优采样率。

6 异构多传感器污染传感与自适应

异构传感器网络是指无线节点配备多种不同类型传感器（如音频、视频、加速度等）的网络。近年来，无线设备越来越多地配备了多模态传感器。手机和智能手机就是具有多种传感器的无线节点的典型示例。这些多模态传感器节点正越来越多地被用于灾后恢复应用 [60, 61],地震监测[62, 63],传染病监测[64],等等。在许多此类应用中，传感器读数在空间上、时间上以及不同类型的传感器之间是相关的。一个典型的示例是地震监测场景，其中所需的传感器包括加速度计、音频传感器、摄像头等，这些传感器中的多个可以集成在一个无线设备中。加速度计通常与速度地震仪结合使用，用于测量和记录地面运动的程度或

振动。音频样本还可用于追踪建筑物倒塌的声音。视频和图像可用于构建地震造成损毁的空间视图。在此示例中，三种传感器均测量地面运动这一相同现象的某些方面。请注意，在此示例中，加速度传感器是检测地震的直接传感器，而音频设备和摄像头则是代理传感器。此类代理传感器可靠性较低，因为建筑物倒塌的声音和图像可能由其他灾害（如气旋、飓风等）引起。

本文中，我们将异构多模态感知的概念扩展到供水管网中的污染检测场景。我们的主要目标是探讨上述相关的不同传感器检测能力，以高效且协同地报告污染事件，尤其是在夜间低能耗时段。在供水系统中，传感器之间的相关性可能由两个因素引起。第一个因素是空间相关性，它源于供水管网拓扑结构和水流。例如，考虑图9，其展示了一个Y型接头，水从管道1流入，并分配至管道2和3。假设每个节点处都部署了一些传感器（例如铁锈、氯、 pH值等）。当管道1发生污染时，该污染会传播至管道2和3，由于水流产生的空间相关性，因此无需在节点1设置传感器。第二个因素是传感器间相关性，即不同类型传感器之间的固有依赖关系。例如，余氯和pH值之间存在相关性（或“兼容性”），在短时间内可以通过其中一个推断出另一个的浓度。由于节能在大多数传感应用中至关重要，利用空间相关性和传感器间相关性可以使传感器周期性开关，同时仍能有效完成传感任务。

在这种多传感器环境中，协作采样在异构无线传感器网络中的应用具有两方面优势。首先，需要利用传感器之间的传感器间相关性，关闭部分传感器模块，同时仍保持合理的覆盖范围。其次，可以利用不同连接点处不同无线设备的空间和相关检测能力，降低能量受限节点的采样率，并通过提高高能量节点的采样率进行补偿。

6.1 各种水质指标

美国环保署已定义了12类潜在水污染物，相关报告见参考文献 [67,68]。表 3列出了这些污染物类别及其示例。由于潜在污染物的数量相当多，为每一种污染物部署对应的独立传感器成本高昂且繁琐。一个更实用的方案是使用测量指示性或替代参数的传感器，以检测异常水质，进而进行可能的污染评估指或替代参数来检测异常水质，以进行可能的污染评估 [67]。参考文献 [67]中报告称，通过测量三种常见的替代参数——余氯、电导率和总有机碳（TOC），可以检测出12类污染物中的10类[68]：余氯、电导率和总有机碳（TOC）。

上述研究发现，游离氯是污染最敏感的指标，其浓度在远低于致死浓度一到两个数量级时，便已表现出与基线值显著不同的变化。这些研究还表明，水中的总有机碳（TOC）是检测多种有机化合物存在的一个重要替代指标，其灵敏度范围从∼0.5mg/L 到超过 1mg/L，具体取决于基线水平和变异性。为了测量水中的总有机碳（TOC），有时会使用 254纳米波长的紫外线吸收法[67]。这是因为有机物含量会吸收紫外线，因此测量紫外线吸光度可以反映水中有机物的浓度。

除了氯和总有机碳外，电导率也被发现对某些无机污染物和金属有轻微响应，尽管与游离氯余量和总有机碳相比，其响应较弱。然而，电导率传感器有可能检测到不会触发氯或总有机碳响应的一些污染物。通常情况下，电导率传感器在较高浓度下对污染物产生响应。

除了游离氯余氯、总有机碳和电导率之外，其他水质参数对各种污染物类别也具有敏感性。氧化还原电位（ORP）通常表现出与余氯相似的行为，可用于验证余氯变化的观察结果。pH值对于理解水体的水化学性质至关重要。浊度或水的浑浊程度作为污染的主要指标具有波动性和不可靠性，但结合其他测量参数时，可能有助于理解水质污染情况。这六个参数构成了水质监测传感器网络中通常包含的最常见的一组替代指标。[67].

上述六个参数无法检测的两类污染物是化学战剂和植物毒素。挥发性有机碳（VOC）分析仪可用于检测和识别此类污染物的特定化合物。

定义与假设：我们假设，在供水系统（WDS）中部署了少量配备多种异构传感器的无线设备，用于监测目的。由于一个无线设备上安装有多个传感器，我们将整个设备称为一个节点，而用词语传感器来描述附着在该节点上的各类传感器（如氯、OPR、pH值等）。我们假设污染物可能通过某些泄漏或人为方式，经由不同的管道段进入系统。一次污染事件指某一类型的污染物通过特定的管道段进入系统。因此，若在一个包含l根管道的供水系统中考虑c种类型的污染物，则总共假设有 E= c ·l个污染事件存在于该系统中

供水系统。我们考虑一个无环的供水系统，其中污染事件根据水流方向在下游连接点传播。我们忽略了独立传感器在不同污染物浓度下的响应时间，这将是我们未来的研究重点。

在本文中，我们仅考虑那些主要为无害且由管道中的缓慢渗漏或积聚所导致的污染物。对于因恐怖主义行为注入或意外有毒化学品泄漏等危及生命的高毒性物质，需要使用专门为此类污染物设计的传感器进行监测，这些传感器以固定频率采样，而不考虑节能问题。此类高毒性物质的检测通常需要停止供水并冲洗整个系统，这不在本文的讨论范围内。

6.2 提出的自适应方案

通常，位于附近区域的一组传感器节点在污染检测能力方面可能存在显著的相互依赖性。我们可以将这些节点视为在博弈论意义上形成一个联盟，该联盟可用于实现性能提升。联盟可以通过在不同管道段模拟污染来构建，使用任何商业模拟器（例如Water‐GEMS） [47]并通过分析单个节点检测能力之间的相互依赖性来确定，即如果联盟中的任一管道段发生污染，至少有几个传感器节点能够检测到该污染。此外，联盟内部的污染需要快速向下游方向传播，以便下游的传感器能够迅速响应并报告污染情况。联盟成员可根据各个节点的能量可用性协作调整其采样率，或关闭部分传感器，例如，采集能量较低的传感器节点采用较低的采样率，而能量较高的节点则以更高的采样率进行补偿。

我们假设时间被划分为 区间，每个区间为 Φ个时间单位。采样率和传感器的活动在每个区间内周期性地更新，具体如下。所有节点在每个区间内持续跟踪其平均采集能量。基于历史能量分布，它们使用归一化最小均方（NLMS）自适应滤波器预测下一区间的预期采集能量。各节点通过 信标消息广播该区间的预测能量可用性以及超级电容器的存储能量。汇聚节点随后利用这些信息来自适应调整各个传感器的活动或其采样率。下面，我们提出两种版本的采样率自适应方案。第一种方案称为 异构协同采样(HCS)，旨在使节点的采样率与其在某一区间内的预测能量预算相匹配。我们还提出了HCS的另一种版本，称为 高级HCS（AHCS），该版本考虑了超级电容器的存储容量以及由于存储不足导致的能量损耗，并在更小的时间尺度上进行处理。问题建模所用的符号列于表 4中。

6.3 异构协同采样（HCS）

在接收到所有传感器节点的能量可用性信息后，汇聚节点构建采样率自适应问题，以在满足所需能量约束的条件下最大化某个效用函数。假设有 N个节点组成一个联盟，并且共有 S种不同类型的传感器。需要注意的是，不同传感器的检测能力可能是相关的。例如，在存在草甘膦的情况下，氯、pH值和氧化还原电位传感器的读数会同时发生变化。图10展示了代理感知的概念框图，其中顶点P1, P2, P3表示污染物的类型（如草甘膦、二甲基亚砜），而S1, S2, S3, S4表示用于感知污染物特性的不同传感器（如氯、pH值和氧化还原电位传感器）。它们之间的边是权重weights，反映了传感器对污染物感知的准确程度。

然而，联盟中位于污染事件下游方向的一些节点可能会因污染物的传播而做出响应。由于联盟内传感器节点的检测能力高度相关，这些传感器节点可以根据其可用的收集能量，在彼此之间共享数据采样任务，以降低能耗。

∀t; 4: V ={ϕ}; 5: 对每个传 感器 i ={1, 2,. . . , S}执行 6: 如果 rm i < Rm ·x m i 成立 7: 分配 rm i = Rm · x m i ; 8: V = V ∪i; 9: Δ= Em −∑ir m i(e i+ c i); 10: 对每 个传感器 j V 执行 11: r m j = r m j + ∑k θ kmj∑iV ∑k θkmi · Δ (ej+cj ) ; 12: 结束 循环 13: 结束如果 14: 结束循环 15: V ={ϕ}; 16: 对每个传感器 i ={1, 2,. . . , S}执行 17: 如果 rm i > RM ·x m i 成立 18: 分配 rm i = RM ·x m i ; 19: V = V ∪i; 20: Δ= Em −∑ir m i (e i + c i ); 11: 对每个传感器 j V 执行 22: r m j = r m j + ∑k θkmj∑iV ∑k θkmi · Δ (ej+cj ) ; 23: 结束循环 24: 结束如果 25: 结 束循环 26: 返回 rm i ∀m)

能量。我们通过考虑以下因素来定义报告污染事件k的总体效用： 传感器采样和报告的速率，即rmi∀ i,m。随着传感速率的增加，整体检测能力也随之提高。 •它们对应的污染检测概率表示为pkmi∀i,m, k。如果某个传感器由于污染事件k显示出显著偏差，则提高其采样率将增强对该污染事件效用函数的贡献。pkmi在以下情况下被视为零：(a) 节点m不在事件k的下游，或 (b) 从污染点到节点m的近似水流传播时间超过某一阈值。条件(b)非常重要，因为污染事件需要在合理的时间内被检测到。 考虑到这两个因素，传感器报告事件k的有效速率由ek=∑ S i=1∑ N m=1p km i · rim给出。因 此，通过将事件k的效用建模为Uk(ek) = log(