交通传感器数据实时清洗

交通传感器网络中的实时数据清洗

摘要

通过部署物联网（IoT）技术，城市环境的许多方面都可以实现实时监控。在智慧城市中，交通出行、污染、停车、垃圾、照明可以通过低成本传感器网络进行控制和管理。传感器实时生成的此类大数据流需要采用适当的技术进行处理，以即时检测错误测量。
本文中，我们实现了一种快速的数据清洗过程以消除交通传感器故障。然后，我们提出了一种交通模型，该模型充分利用了交通传感器测量到的异常数据检测结果。在实际案例场景中的实验表明，异常检测能够进一步提升交通模型在模拟真实城市交通方面的性能。

索引术语

IoT技术，异常检测，大数据，STL分解，数据清洗

一、引言

传感器网络基础设施在智慧城市中被广泛用于交通管理，以监控和分析交通状况。由于交通传感器安装在道路表面下方，无法持续进行维护，因此传感器可能出现故障。
为流式时间序列提供实时异常检测具有重要价值，因为它使我们能够在时间敏感的过程中及时自动识别传感器故障。
交通仿真软件是进行道路交通分析和城市交通模拟的重要工具。通过将交通传感器数据作为输入，可实时运行交通仿真，以建模整个城市背景下的交通流量。为了获得有意义的结果，应尽可能缩短传感器数据采集与模型输出生成之间的延迟。因此，对输入数据中的异常必须在最短时间内完成检测。本文旨在提出一种方法，用于实时检测由传感器故障引起的异常，并将其从交通模型的输入中去除。
所讨论的用例为中等规模的意大利城市摩德纳的交通传感器网络，该城市人口密度为 1017 inhabitants/km²，公共道路长度超过 900 km，面积为 184727 inhabitants。
来自约400个交通传感器的数据被输入到一个定制化交通模型中，以实时提供整个城市道路网络的交通数据。通过比较模型在包含与排除异常传感器观测数据情况下的输出结果，评估了数据清洗过程所带来的改进效果。
近年来，针对时间序列数据的数据清洗技术已被讨论、分类和比较。在[1]中使用了基于约束的算法，重点关注速度约束。随后提出了时间序列异常检测算法：自回归积分滑动平均模型（ARIMA）、长短期记忆网络（LSTM）、基于密度的空间聚类算法（DBSCAN）以及生成对抗网络（GANs）。时间序列异常检测可通过多种技术实现：统计方法、机器学习算法和深度神经网络。在[2]中，对上述三类中的不同单变量异常检测方法在公开可用的数据集上进行了比较和评估。此外，使用 Loess的季节‐趋势分解（STL）也被用于异常检测，并与其他方法（如四分位距（IQR））结合使用。在[3]中提出了一种双层异常检测方法：首先研究时间序列的非平稳性和周期性变化，然后利用环境中可观测的变量来解释任何额外的信号变化。[4]的作者将STL分解与季节性自回归积分滑动平均模型（SARIMA模型）相结合，以检测非周期性时间序列中的异常。最后，[5]中描述的方法将 STL分解与扩展孤立森林相结合。我们的方法将STL分解与来自传感器数据的基于约束的滤波器相结合，这一方法在前述方法中尚未出现。该滤波器能够识别出STL分解技术无法识别的异常值。
本文其余部分结构如下。第二节概述了用例背景。第三节描述了所采用的方法：数据清洗过程（第四节），包括数据过滤和异常检测，以及排除异常的交通仿真生成（第五节详细描述）。第六节讨论了在实际案例场景中应用所述方法所获得的结果。第七节勾画了结论与未来方向。

II. 背景

A. 传感器网络

智慧城市利用传感器向公众、企业、城市管理者和其他智能系统共享信息。
对于交通管理，存在大量利用不同技术的传感器，能够确定通过城市道路的车辆数量（例如感应线圈、预制线圈、压力传感器、雷达、视频）。其中感应线圈是最常用的传感器，这种技术50年前就被引入，至今仍广泛存在于许多城市。感应线圈传感器由导线“绕制”成环形线圈，并安装在道路表面内部或下方。在摩德纳，感应线圈检测器分布在不同位置，通常靠近交通信号灯。这些传感器根据数据提供商的不同，以不同的频率收集交通数据（即车辆数量和平均速度）。在摩德纳，我们有两个交通数据提供商：位于城区的传感器由市政府管理，每1分钟发送一次数据；而省级和区域道路的传感器归地区所有，其数据由一家区域性公司以15分钟的频率进行分发。
传感器数据被收集并用于在交通模型[6]–[8]中模拟车辆的实际路线。摩德纳传感器地图¹显示了摩德纳市内所有可用的交通传感器，其中绿色的传感器作为输入用于交通模型。其余未被纳入交通模型输入的传感器可能是不可靠的传感器（例如，在日时间段内仅获得少量测量值，或其大部分测量值为零值），或是位于市区以外道路的传感器。

¹ 摩德纳传感器地图：https://trafair.eu/modenasensormap/

B. 传感器数据采集

来自两个数据提供商的传感器数据被实时收集到 PostgreSQL数据库[7]中。该数据库使用了两个扩展：PostGIS用于处理地理空间数据，Timescale用于在处理大量数据时提升性能。从2018年9月至今（2020年6月），该数据库已收集了摩德纳市交通传感器记录的超过2.65亿条观测数据。每条观测数据包含一条记录，内容为传感器标识符、传感器测量的流量、速度、车辆类型（仅限省级和区域级传感器）以及测量的时间间隔，并存储在数据库中。解析交通传感器数据并将其存储的流程是用Python实现的。

III. 提出的方法

我们的目标是通过对来自交通传感器的数据进行异常识别，从而在交通仿真模型的输入中排除这些异常，实现对交通观测数据的数据清洗。如图1所示，该方法包含以下几个步骤：（1）过滤具有异常流量‐速度相关性的观测数据（这些观测数据在数据库中被标记为“已过滤”）；（2）通过用平均值替换“已过滤”的观测数据进行异常修复；（3）通过STL分解进行异常检测；（4）通过去除异常生成交通仿真模型的输入；（5）运行模型。

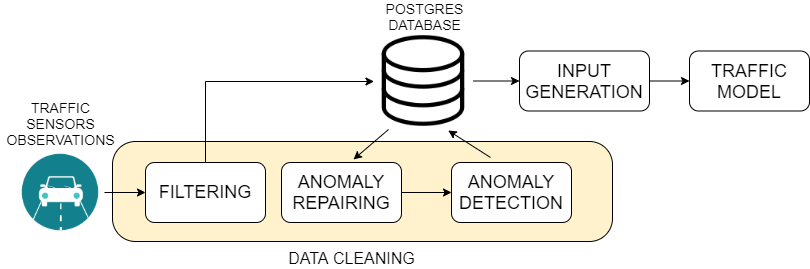
将通过比较交通模型在输入数据中排除异常或包含异常时的性能，来研究数据清洗所带来的影响。

IV. 数据清洗

数据清洗的过程包括提出的方法中的前三个步骤，如图1所示，分别为过滤、异常修复和异常检测。在接下来的子章节中，将详细描述这些步骤。

A. 流量-速度相关性过滤器

交通传感器提供的流量和速度值彼此之间具有很强的相关性。假设一个传感器位于单车道上，如我们的情况所示，在固定时间间隔内，以特定平均速度通过该传感器的车辆数量存在一个上限。该数值由以下公式给出：

$$
\text{num vehicles} = \frac{\text{speed}[Km/h] \times 1000}{\text{vehicle length} + \text{safe distance}[m]}
$$

其中speed是传感器提供的平均速度，vehicle length是不同类型车辆的平均长度，safe distance是基于车辆速度应在每对车辆之间保持的安全行车距离（按 speed/3.6计算）。
num vehicles的值表示基于车辆平均速度在一小时内可通过的最大车辆数。允许的流量值的上限是将num vehicles的值根据观测对应的时间间隔（分别为1分钟或15分钟）除以60或4得到的。如果传感器提供的流量高于此数值，则该观测被视为异常；因此，将其标记为“已过滤”。
我们实时应用此过滤器，即每次将观测数据存储到数据库时，都会包含“已过滤”或“未过滤”的信息。我们将车辆长度的值设置为4。

B. 异常修复

大多数传感器每分钟提供一次测量值，并以此时间间隔进行过滤。然后，数据需要每15分钟聚合一次，以便用于交通模型。因此，一旦传感器测量值被标记为已过滤，就不能简单地从交通传感器观测中移除。为了评估更大时间间隔内的聚合流量，流量值会被累加，因此移除观测数据相当于将其视为零。
然而，这相当于假设在该时间间隔内没有任何车辆正在通过。这一假设并不正确，因此需要找到一种替代解决方案。由于过滤观测值中的测量值不可靠，因此考虑同一传感器在邻近时间区间内的观测值进行替换。我们决定采用15分钟的时间间隔。过滤观测值的流量将被该传感器在同一时间间隔内测得的可靠（未过滤）流量的平均值所替换。
聚合速度更难评估；由于传感器提供的测量值是平均速度，我们假设过滤后的观测数据的速度等于在15分钟时间间隔内仅考虑未过滤测量值的加权平均速度。当某个传感器在15分钟时间间隔内的可靠观测少于2个时，该异常修复技术无法应用。此时，该15分钟时间间隔的聚合流量和速度被归类为异常，并且不会用于后续步骤中。

C. 通过STL分解进行异常检测

使用Loess的季节‐趋势分解（STL）是一种将时间序列分解为三个组成部分的滤波过程：趋势、季节性和余项（也称为残差）[9]。将时间序列分解为各组成部分有助于异常检测。
加性分解考虑了由以下公式描述的时间序列模型：

$$
y_t = \tau_t + s_t + r_t, \quad t = 1, 2, …, N
$$

其中 $ y_t $ 表示在时间 $ t $ 的观测值，$ \tau_t $ 是时间序列中的趋势，$ s_t $ 是周期为 $ T $ 的季节性信号，而 $ r_t $ 是余项分量。
趋势分量包含数据中的低频变化，具有非平稳的长期变化，即持续增加或减少。而季节性分量则由数据在基线附近的变化（周期性模式）构成。通常情况下，趋势比季节性变化更快。其余的变化被归入残差中。
通过迭代多次应用局部加权回归（Loess平滑器）来实现时间序列分解。这些应用的结果是一条表示原始时间序列平滑的曲线，该曲线在计算时考虑了邻域内可变数量观测值的值。
STL 的一种变体是 RobustSTL [10]，它被定义为一种鲁棒且通用的季节性‐趋势分解方法，能够从具有长季节性周期和高噪声的数据中提取季节性。RobustSTL 所采用的方法包括四个步骤：
1) 通过应用双边滤波并利用窗口内 2H+1个具有相似值的观测数据来平滑时间序列，实现去噪；
2) 使用最小绝对偏差（LAD）损失结合稀疏正则化进行趋势提取；
3) 通过非局部季节性滤波进行季节性提取，该方法考虑时间维度上不同距离及季节性值加权的 K个季节性邻域中的 2H+1个观测数据；
4) 通过计算季节性均值进行最终调整，该均值被添加到趋势中并从季节性中移除。

需要向算法提供若干配置参数：周期 $ T $（即每个季节性周期内的观测数量）、步骤1中双边滤波器的超参数（dn1和 dn2）、邻域数量（H）、趋势提取的正则化参数（reg1和 reg2）、过去的季节样本数量（K），以及季节性提取步骤中双边滤波器的超参数（ds1和 ds2）。
每一步之后，通过移除该步骤中提取的成分来更新输入信号。在第4步之后，重复这些步骤，直到当前迭代的余项与前一次迭代的余项之间达到收敛。收敛性通过以下公式计算：

$$
\text{convergence} = \sqrt{(r_i - r_{i-1})^2}, \quad i = 1, 2, …, N
$$

其中 $ r_i $ 是迭代 $ i $（当前迭代）时的余项，$ r_{i-1} $ 是迭代 $ i-1 $（前一次迭代）时的余项。如果收敛程度高于阈值，则继续进行下一次迭代；否则，认为分解结果已确定。在后一种情况下，结果为3个时间序列，分别表示趋势、季节性和残差。
分解完成后，可以通过分析残差曲线并使用不同的方法来检测异常。一种解决方案是应用四分位距（IQR）。
在确认残差符合正态分布（零均值和单位方差）后，计算第一四分位数（Q1）和第三四分位数（Q3）。上下限通过以下公式求得：

$$
\text{lower fence} = Q1 - k \times IQR \
\text{upper fence} = Q3 + k \times IQR
$$

其中 IQR是第三四分位数与第一四分位数之差，$ k $ 是乘数。乘数值越高，检测到的离群值越少。$ k $ 的取值取决于我们想要检测的离群值类型；较高的 $ k $ 值用于检测极端离群值。残差值低于 lower fence 或高于 upper fence 的观测数据为离群值。
我们设置了 $ n $ 个进程，用于对传感器数据进行实时的STL分解，其中 $ n $ 是我们数据集中传感器的数量。实际上，每个传感器的时间序列分解相互独立。我们采用了一个在线提供的 RobustSTL 实现²。
每15分钟执行一次分解。用作输入的时间序列是通过对特定传感器的一周流量测量值的对数按15分钟进行分组生成的。

² https://github.com/LeeDoYup/RobustSTL

应用IQR方法后，仅考虑最近15分钟内的异常，因为之前时间间隔中的异常已被之前的分解过程提取。我们选择每15分钟聚合一次观测数据，因为交通模型的输入需要这种方式，具体将在第五节中描述。选择使用一周的观测数据是在为分解提供足够上下文与快速获得结果之间的一种权衡。事实上，一个月数据的分解所需时间（平均约12分钟）远大于一周数据的分解时间（平均约15秒）。因此，我们将周期 $ T $ 设置为一周内观测数量除以7。经过多次实验，我们决定将其他配置参数设置如下：dn1=1, dn2=1, H=3, reg1=10, reg2=0.5, K=1, ds1=50, ds2=1。
最后，我们将IQR方法中 $ k $ 的初始值设为3，以避免真正的异常交通状况被标记为异常。在IQR方法中将 $ k $ 的值设为3，以便排除确实是异常的观测数据。当使用更低的 $ k $ 值时，我们注意到大量观测数据被视为异常，但通过检查流量和速度值发现它们似乎并非真实异常。这可能是因为我们的传感器位于交通信号灯附近，因此可能出现峰值，这些峰值可能与交通信号灯变为绿色有关。

V. 交通模型

交通仿真模型是有助于规划、管理和分析城市交通的数学工具。动态交通模型能够创建交通状况随时间变化的详细演化过程。所采用的模型是一种动态微观模型。在微观模型中，每辆车的移动行为由个体决策决定，这些决策依赖于：与其他车辆的交互、道路环境以及交通信号。车辆的移动不依赖于宏观或概率规律。模型中的每一辆车都是具有自身目标和行为特征的独特实体，并具备与其他实体交互的能力。我们采用了开源微观仿真模型SUMO³，并配置该模型以根据交通传感器数据生成车辆行驶路线，如[8]所述。该模型以交通传感器的测量值为输入，生成摩德纳市各条道路上的车辆计数及其平均速度的数据。

A. 输入生成

车辆路线的创建考虑了按15分钟时间间隔聚合的实际交通传感器数据。该模型包含称为校准器的对象。校准器是 SUMO套件的一部分，类似于虚拟交通传感器，其根据路面传感器的实际测量值进行校准。每个校准器可生成期望的交通流量，即由与该校准器相关联的传感器所统计的车辆数量。
对于城市中的每个真实交通传感器，在仿真中都会插入一个对应的校准器。交通传感器提供的车辆计数和速度是校准器希望达到的值。如果未向校准器提供特定时间间隔内的交通流量信息，则不会添加或移除车辆。相反，若提供了需要达到的车流信息，校准器将通过添加或移除车辆来实现指定的交通流量。因此，从输入数据中清除传感器故障至关重要，以获得更真实的仿真结果。
我们使用开放街图（OpenStreetMap）作为地理数据源来定义道路网络，并将其存储到数据库中。每条道路路段都是由多个点组成的线对象。然后，道路路段被划分为更小的路段，即两个连续点之间的道路部分。

B. 输出

仿真在高性能计算资源上进行。一旦仿真完成，其输出将存储在数据库中。每15分钟收集一次每个车道段（在我们的用例中超过17000个）的流量（辆/小时）和平均速度（米/秒）值。对从多次仿真中获得的交通数据的分析见[12]。此外，针对每个传感器位置提供额外的输出：该点在仿真期间观测到的15分钟聚合车辆计数和速度的时间序列。

C. 交通模型评估

交通模型的主要目标是模拟出与城市街道中实际观测值足够接近的交通流量。模型输出的是在交通传感器所在确切位置统计到的车辆数量。在交通传感器所在位置模拟出的车辆数必须与真实车辆计数进行比较。即使使用了交通传感器数据来驱动模型，校准器也并不总能插入所需数量的车辆：仿真中插入的车辆数与真实传感器计数的车辆数可能存在差异。这种情况主要发生在传感器测量到极高的流量时，其对应的校准器会插入大量车辆，导致仿真中出现拥堵，从而阻止附近其他校准器再添加更多车辆。这种极高的流量可能是由传感器故障引起的，进而影响整个仿真的性能。
[13]中描述了所提出交通模型的评估方法。对于每个用作模型输入的传感器，通过三种不同指标计算两个时间序列之间的距离，即传感器观测到的实际流量与模拟流量：快速动态时间规整（DTW）、点对点距离（PWD）和计数时隙距离（CTD）。
使用FastDTW评估DTW，FastDTW是DTW的一种复杂度较低的版本，如[14]所述。该指标允许序列在时间轴上拉伸，能够找到时间序列中的对应区域，并且可以容忍噪声、时间偏移以及Y轴上的缩放[15]。PWD被评估为仿真中所有时间步长内的测量流量与模拟流量之间的差值求和。我们不使用绝对距离，而是根据符号对距离进行求和，因为后续的时间间隔可能会弥补前一个时间间隔中观察到的差异。CTD 是指测量流量与模拟流量之差大于每分钟2辆车的时间间隔数量。
根据“对齐”和“未对齐”两种情况，结合所提出的指标对校准器进行了分类。若校准器的实测数据与模拟流量之间的DTW距离大于1200，PWD大于30，且CTD大于仿真总时间步长的一半，则该校准器被视为“未对齐”。
被分类为“未对齐”的校准器无法正确插入输入所要求的预期车辆数量。
为了评估仿真的性能，我们需要生成一些指标，这些指标可以通过一个唯一值来总结在每个传感器位置观察到的距离。我们定义了5个指标，用于比较在考虑或排除异常情况下进行的仿真：对齐校准器的百分比、平均均方根误差（RMSE）、平均DTW减少量、平均PWD减少量、平均CTD减少量。对于每次仿真，将被分类为对齐的校准器数量除以校准器总数，以获得对齐校准器的百分比。分别计算包含异常的仿真和在同一时期排除输入中异常的仿真所得到的对齐校准器百分比值。较高的百分比意味着更多的对齐校准器，从而表明模型性能的优化。在每个传感器位置评估实际测量值与模拟流量之间的时间序列均方根误差（RMSE），并取平均值。针对包含和排除异常的每次仿真，分别计算平均RMSE值。较高的平均RMSE表示更大的误差，因此意味着模型性能的下降。在两个仿真中，于每个传感器位置评估实际测量值与模拟流量时间序列之间的DTW距离，方法如下：

$$
\frac{1}{N} \sum_{i=1}^{N} \left( \text{DTW}(m_{i,1}, s_{i,1}) - \text{DTW}(m_{i,2}, s_{i,2}) \right)
$$

其中 $ m_{i,1} $ 是第一个仿真中传感器 $ i $ 的实际测量时间序列，$ s_{i,1} $ 是传感器位置的模拟流量，$ N $ 是传感器总数。平均 DTW减少量通过比较两次仿真的性能获得：一次考虑异常，另一次从输入中排除异常。评估两次仿真在每个位置观测到的DTW距离之间的差异，并将这些差异的均值称为平均DTW减少量。如果该值为正值，则表示距离减小；否则，第一次仿真的表现更优，因为距离增大了。类似地，通过评估两个仿真在相同周期内每个传感器的PWD距离或CTD距离的差异，得到平均PWD减少量和平均CTD减少量。

VI. 实验与结果

为了验证我们方法的有效性，本文描述了将第三节介绍的方法应用于2019年4月交通数据所得到的结果。
2019年4月，来自交通传感器的观测数据数量为1300万条，涉及338个传感器。
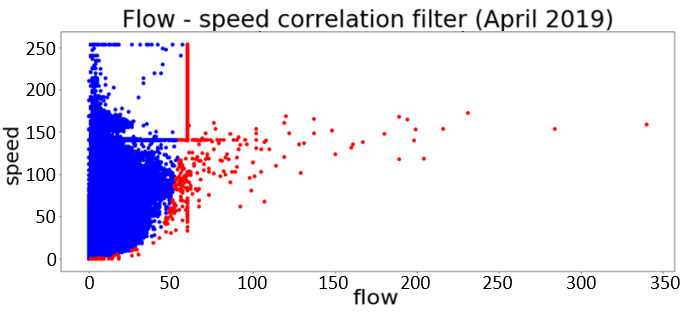
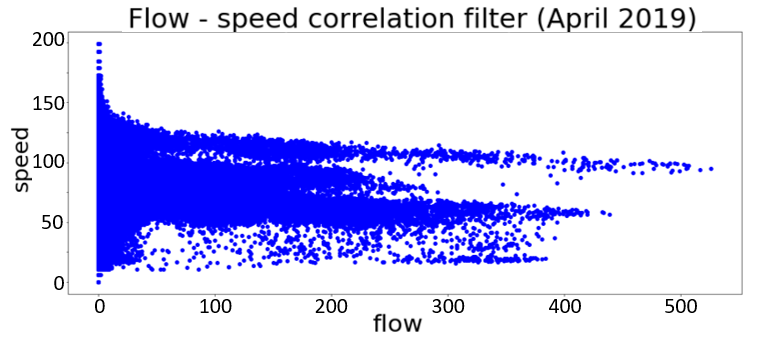
使用流量‐速度相关性过滤器，共过滤出450845个观测数据（占总观测数的3%）。这些过滤后的观测数据与259个传感器相关。图2中的散点图显示了2019年4月城市传感器（图2a）和市区以外省级或区域道路上传感器（图2b）的流量和速度值；红色点为过滤后的观测数据。可以看出，在来自省级和区域传感器的数据中未发现过滤后的观测数据。在图2a中，我们可以注意到，对于低流量值，极高的速度值被视为“非异常”。实际上，如果没有交通流（低流量），车辆可能会高速行驶，尤其是在夜间。然而，对于较高流量值，极高车速的观测被视为“异常”并被过滤。过滤后的流量值将按照第四节B部分所述进行替换。

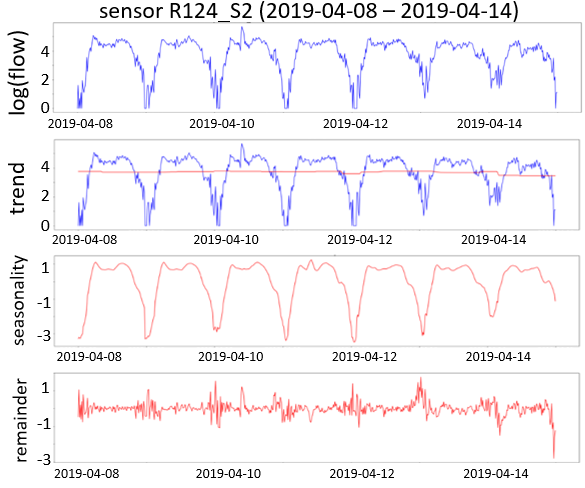
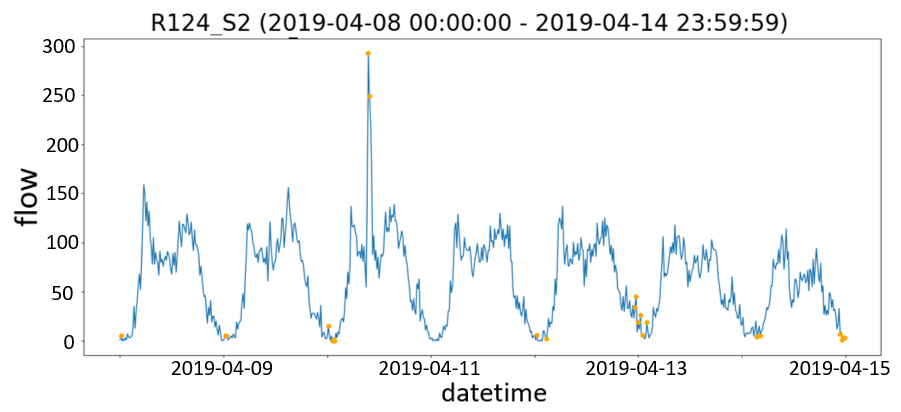
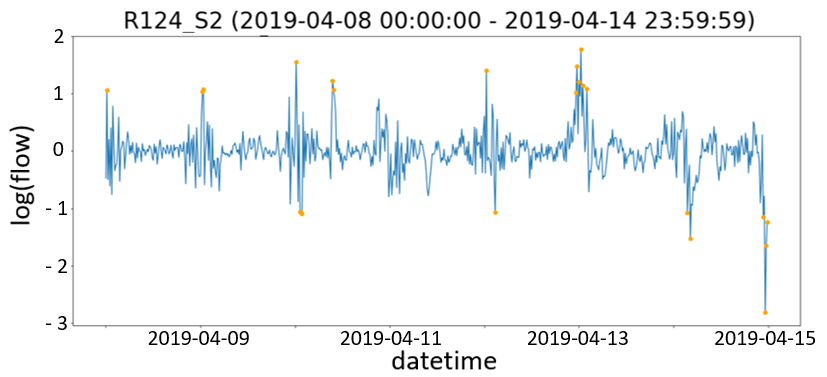
在对每分钟已过滤数据应用异常修复阶段后，所有传感器观测数据将每15分钟聚合。通过对聚合交通数据应用IQR方法进行STL分解，检测到与310个传感器相关的13932个异常（占观测数据的不到0.1%）。图3a显示了一个分解示例，该示例涉及一个传感器在2019年4月8日至2019年4月14日之间的观测数据。时间序列分解将序列视为趋势、季节性和余项（也称为噪声）成分的组合。图3b在所有观测数据的时间序列上绘制了以橙色突出显示的异常；而图3c则在时间序列的余项成分上展示了异常。

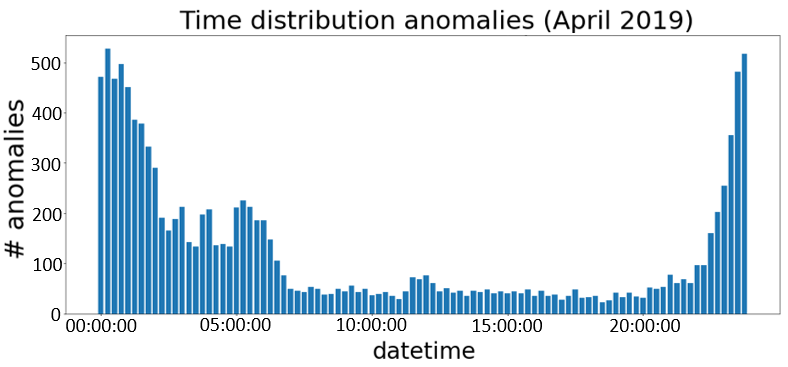
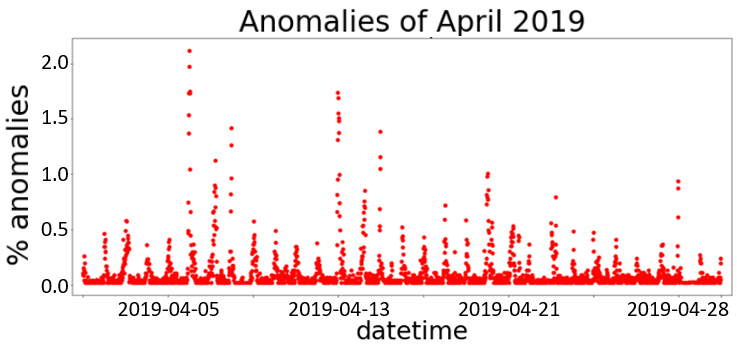
分析异常的时间分布，大多数异常在夜间被检测到，如图4所示。图5显示了2019年4月每天的异常百分比：在某一天（2019年4月6日），异常百分比超过了2%。

一旦STL检测到异常，这些异常将被存储在数据库中。每个异常都与聚合观测的15分钟时段及其所属的传感器相关联。
对于2019年4月的每一天，进行了两次仿真。第一次仿真使用所有可用传感器的观测数据作为输入（未对这些数据进行数据清洗）。而对于第二次仿真，则对交通数据执行了数据清洗过程，并从输入中移除了异常观测数据。无需进行异常修复，我们只需将异常观测从交通模型的输入中删除，校准器在模拟车辆时会考虑之前的和后续的参考值。在表I中，列出了2019年4月每一天的所有评估指标。

对包含异常输入数据的仿真所评估的指标用后缀‘before’标记，而对排除异常后仿真的指标则用后缀‘after’标记。第五节第V‐C节中描述的对比指标，是以未进行输入数据清洗过程的仿真作为第一次仿真，以输入中不含异常的仿真作为第二次仿真来进行评估的。观察2019年4月的数据，在77%的每日模拟中，排除异常后对齐校准器的百分比有所增加（如表I第三列所示），仅有3天对齐校准器的数量减少。在73%的情况下，平均RMSE误差减小（如表I第五列所示）。如果平均DTW减少量为正值，则说明排除异常后异常会降低平均DTW距离。在仅有60%的每日模拟中，平均DTW减少量为正值（如表I第六列所示），这可能与从输入时间序列中排除异常有关，因为DTW对缺失值敏感。其他指标不受缺失值影响，因为它们仅评估每个时间间隔内数值对之间的距离，当某个值缺失时，该距离不参与计算。在60%的每日模拟中，平均PWD减少量为正值（如表I第七列所示），这意味着在大多数天数中，数据清洗过程降低了平均PWD。在90%的每日模拟中，平均CTD减少量为正值（如表I第八列所示），因此，在模拟流量与实际测量值之间的距离大于2 (veh/minute) 的时间间隔数量显著减少。83%的天数在5个指标中至少有3个表现出改善。对于每一天，计算了已过滤的一分钟数据数量以及使用STL检测到的异常数量。过滤值和异常数量最多的日期通常表现出更好的性能（例如，见表I中的4月5日、6日和20日）。为进一步探究性能提升的原因，观察了受影响较大位置的测量值和模拟流量的时间序列。图6显示了4月1日前后（保留输入中的异常与排除异常）实际测量值与模拟流量的对比，表明3个传感器位置的性能受到显著影响。在数据清洗过程之前，位于R137 S11、R047 S4和R027 SM125传感器位置的校准器无法正确跟踪实际测量值：R137 S11在某些时间间隔出现极高的流量，R047 S4在大部分仿真时间内流量为零，而R027 SM125则无法跟随实际仿真后半段的流量。基于这些原因，它们均被分类为未对齐校准器。经过数据清洗过程后，测量数据与模拟流量之间的相似性上升，校准器被分类为对齐。

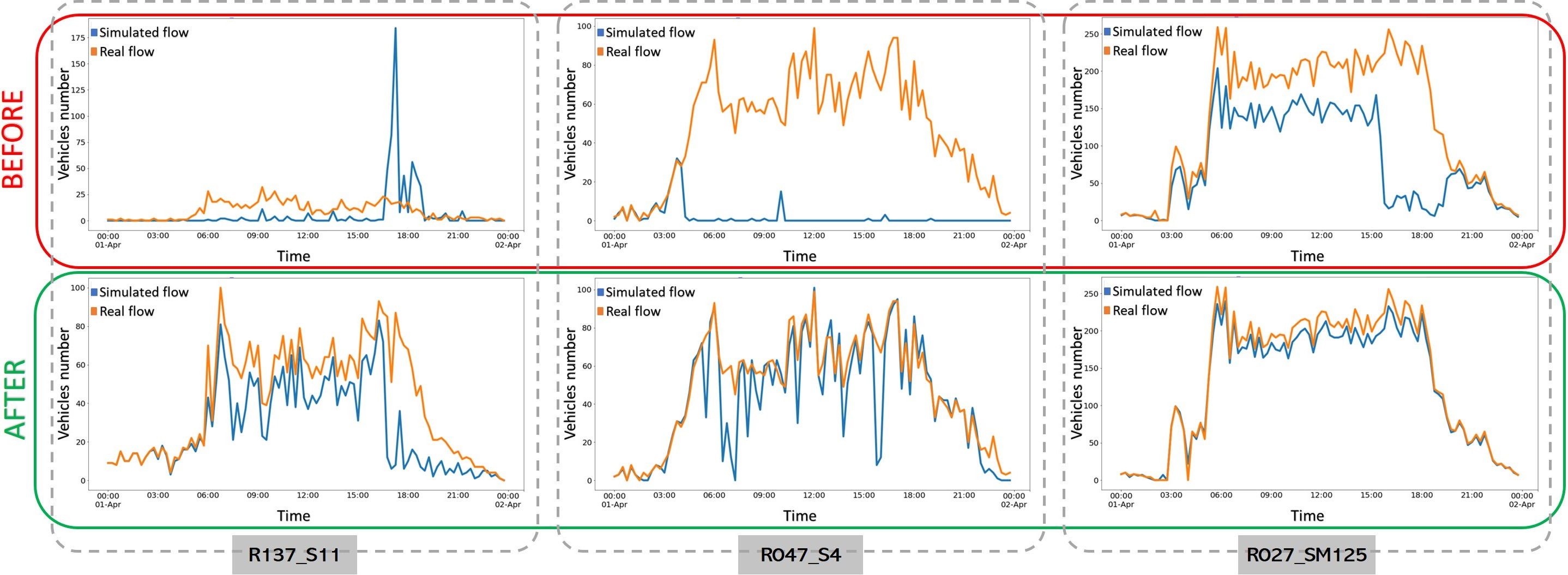
最后，比较了仿真输出结果（每个道路路段的流量和速度）。由于我们移除了被检测为异常的高流量值，预期结果是车辆总数减少。然而，车辆总数在全局范围内增加，并且57%的道路路段日均车辆总数平均增加。仅有11%的道路路段的日平均速度差异的绝对值大于 10 km/h。通过计算因异常检测导致的速度增加和速度降低的数值总和，最终结果表明数据清洗过程加速了仿真中的车辆行驶。受数据清洗过程影响较大的道路路段在流量变化图⁴中显示。在30天中至少有20天日均流量增加的道路用红色表示，流量减少的道路则用蓝色表示。

⁴ 流量变化图 https://trafair.eu/flowvariationmap/

DAY	% Aligned before	% Aligned after	Mean RMSE before	Mean RMSE after	Mean DTW reduction	Mean PWD reduction	Mean CTD reduction	N_filtered	N_anomalies
1	0.86	0.88	28.79	27.50	3.59	1.30	2	9821	404
2	0.85	0.85	28.96	27.28	88.03	2.41	2	9512	589
3	0.83	0.86	30.86	29.37	142.05	0.46	2	9979	603
4	0.84	0.82	29.19	30.15	-131.43	-0.98	4	9931	624
5	0.79	0.81	33.07	30.84	114.21	1.90	1	10188	1026
6	0.82	0.83	27.26	27.08	10.05	2.05	2	11185	681
7	0.91	0.94	19.41	19.12	-14.50	0.85	3	10914	784
8	0.83	0.85	27.83	30.38	6.26	-1.21	5	9678	116
9	0.83	0.81	28.35	28.56	-59.62	-0.39	2	9770	254
10	0.83	0.85	29.28	29.21	66.02	0.84	3	9908	309
11	0.81	0.84	30.04	29.76	73.66	-0.02	3	9758	212
12	0.81	0.79	29.73	32.06	-114.46	-1.19	5	10393	449
13	0.83	0.83	25.84	26.63	-16.12	0.13	3	11092	677
14	0.92	0.94	18.52	18.55	87.98	1.00	2	10664	723
15	0.82	0.84	29.21	30.05	-118.95	0.41	4	9514	114
16	0.83	0.83	30.95	30.15	33.93	1.15	3	9500	274
17	0.82	0.83	31.87	33.02	-67.18	-0.33	3	10001	225
18	0.84	0.84	30.33	28.40	-294.32	1.47	-1	9950	243
19	0.85	0.87	29.83	24.01	-29.10	-1.13	1	10364	336
20	0.84	0.89	23.76	19.87	50.86	0.22	1	10753	600
21	0.93	0.96	15.53	13.00	-42.23	-1.08	1	10262	543
22	0.93	0.96	17.69	13.88	37.32	0.37	0	9980	35
23	0.84	0.89	27.67	20.46	78.73	1.32	-2	10182	371
24	0.80	0.90	29.56	21.98	171.81	1.75	0	10099	176
25	0.91	0.94	18.11	14.35	7.75	0.21	0	10432	250
26	0.82	0.85	29.22	23.17	7.01	0.16	-1	10048	178
27	0.84	0.85	25.28	21.78	-135.00	-0.61	1	11026	139
28	0.86	0.90	29.69	27.63	19.99	-0.46	1	10587	360
29	0.81	0.85	31.49	25.35	28.37	-1.66	1	9694	42
30	0.82	0.84	32.57	25.85	-89.27	-0.50	1	9517	173

表I：包含异常的模拟（之前）与排除异常的模拟（之后）之间的模型评估指标比较

VII. 结论与未来工作

本文提出了一种新方法，用于实时检测交通传感器观测数据中的异常，以提高交通仿真的性能。在真实场景中评估了有无数据清洗过程时交通模型的性能，即使检测到的异常总数仅占输入数据的低百分比，仍观察到显著改进。
本文的核心思想是主要识别传感器故障和恒定误差，因此由真实异常交通状况（如交通事故、道路施工等）引起的异常不应被检测到。基于此原因，我们尽量避免误报，同时接受可能出现部分漏报。在近期，我们将尝试比较不同方法，以区分由传感器故障和真实交通事件引起的异常。
未来的工作还将聚焦于应用结合预测的异常修复技术，以替换通过STL分解检测出的异常数据所产生的缺失值。该方法可在检测到大量连续异常的情况下提升交通模型的性能。