【模板】Tarjan算法求无向图割点

最新推荐文章于 2025-12-27 16:49:17 发布

原创最新推荐文章于 2025-12-27 16:49:17 发布 · 341 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #图论 #c++ #数据结构

这篇博客介绍了图的割点检测算法，利用Tarjan算法进行深度优先搜索来判断图中哪些节点是割点。割点是指在无向图中，删除该点会导致连通块数量增加的节点。文章提供了详细的算法实现，包括代码示例，解释了割点判定法则，并通过样例输入和输出解释了算法的正确性和有效性。

参考视频：董晓算法——Tarjan 割点

题目背景

割点

题目描述

给出一个 $n$ 个点， $m$ 条边的无向图，求图的割点。

输入格式

第一行输入两个正整数 $n, m$ 。

下面 $m$ 行每行输入两个正整数 $x, y$ 表示 $x$ 到 $y$ 有一条边。

输出格式

第一行输出割点个数。

第二行按照节点编号从小到大输出节点，用空格隔开。

样例 #1

样例输入 #1

样例输出 #1

1 
5

提示

对于全部数据， $1\leq n \le 2\times 10^4$ ， $1\leq m \le 1 \times 10^5$ 。

点的编号均大于 $0$ 小于等于 $n$ 。

tarjan图不一定联通。

概念

对图深搜时，每一个节点只访问一次，被访问过的节点与边构成搜索树

时间戳dfn[x]：节点x第一次被访问的顺序
追溯值low[x]：从节点x出发，所能访问到的最早时间戳
割点：对于一个无向图，如果把一个点删除后，连通块的个数增加了，那么这个点就是割点(又称割顶)。

割点判定法则：

如果x不是根节点，当搜索树上存在x的一个字子节点y，满足low[y]>=dfn[x]，那么x就是割点
如果x是根节点，当搜索树上存在至少两个子节点 $y_1,y_2$ ，满足上述条件，那么x就是割点

low[y]>=dfn[x]，说明从y出发，在不通过x点的前提下，不管走哪条边，都无法到达比x更早访问的节点。故删除x点后，以y为根的子树 $s u b t r e e (y)$ 也就断开了，即环顶的点割得掉

反之，若low[y]<dfn[x]，则说明y能绕行其他边到达比x更早访问的节点，x就不是割点了，即环内的点割不掉

当访问已经打上时间戳的节点y时，注意low[x]=min(low[x], dfn[y])，dfn[y]不能换成low[y]，因为这是无向图，能过走回祖先节点，比如下图low[6]显然不能是1，否则dfn[5]=5<low[6]=1

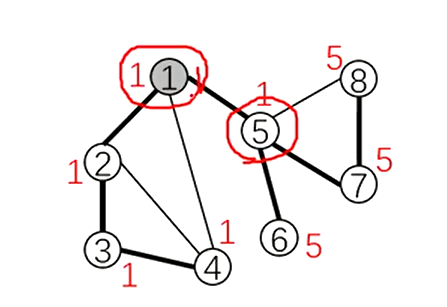
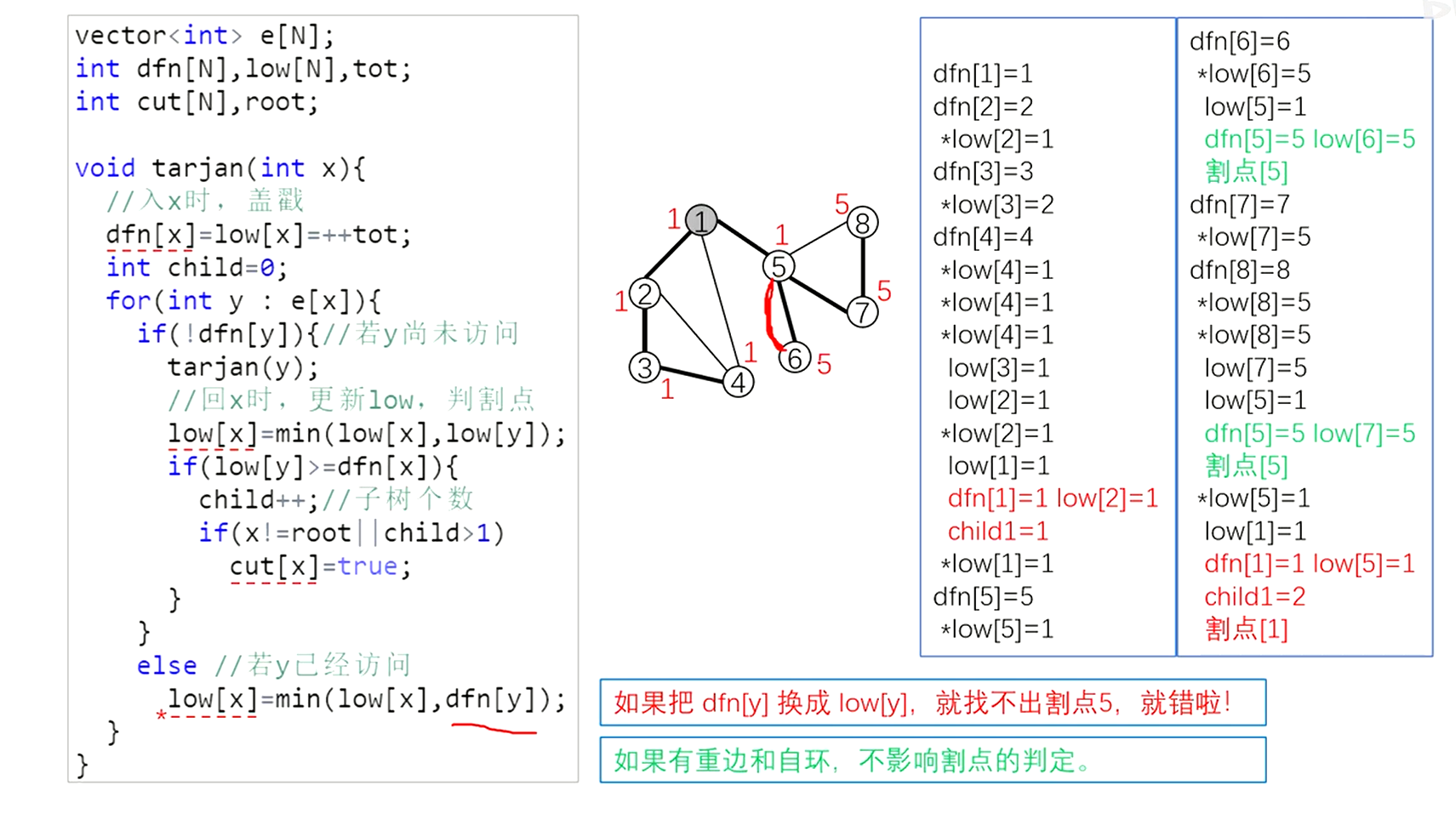
代码

#include<iostream>
#include<string>
#include<vector>
#include<cmath>
#include<algorithm>
#include<set>
#include<stack>
#include<map>
#include<cstring>
#include<queue>
using namespace std;
const int N = 2e4 + 5, M = 1e6 + 5;
int h[N], e[M], edge[M], idx;
int dfn[N], low[N], cut[N], root, tot, cnt;
void add(int u, int v) {
    e[idx] = v;
    edge[idx] = h[u];
    h[u] = idx++;
}
void tarjan(int x) {
    dfn[x] = low[x] = ++tot;
    int child = 0;
    for (int i = h[x]; i != -1; i = edge[i]) {
        int ne = e[i];
        if (!dfn[ne]) {
            tarjan(ne);
            low[x] = min(low[x], low[ne]);
            if (low[ne] >= dfn[x]) {
                child++;
                if (x != root || child > 1) cut[x] = true;
            }
        }
        else low[x] = min(low[x], dfn[ne]);
    }
}
int main()
{
    memset(h, -1, sizeof(h));
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n, m;
    cin >> n >> m;
    while (m--) {
        int u, v;
        cin >> u >> v;
        add(u, v);
        add(v, u);
    }
    for (int i = 1; i <= n; i++) {
        if(!dfn[i]) root = i, tarjan(i);
    }
    for (int i = 1; i <= n; i++) {
        if (cut[i]) ++cnt;
    }
    cout << cnt << "\n";
    for (int i = 1; i <= n; i++) {
        if (cut[i]) cout << i << " ";
    }
    return 0;
}