leetcode刷题日记：104. Maximum Depth of Binary Tree（二叉树的最大深度）和108. Convert Sorted Array to Binary Search

要求一个二叉树的最大深度，可以先求出二叉树的左子树的深度和右子树的深度，比较这两者的大小选取其中大的在加一就是我们要求的二叉树的深度，显然这是递归定义的，递归终止的条件是$root==NULL$递归终止的地方树的深度是0，返回0，有了递归终止条件和递归循环下去的条件，我们可以写出如下代码：

int maxDepth(struct TreeNode* root) {
    if(root==NULL){
        return 0;
    }
    int leftdepth = maxDepth(root->left);
    int rightdepth = maxDepth(root->right);
    return leftdepth>rightdepth?leftdepth+1:rightdepth+1;
}

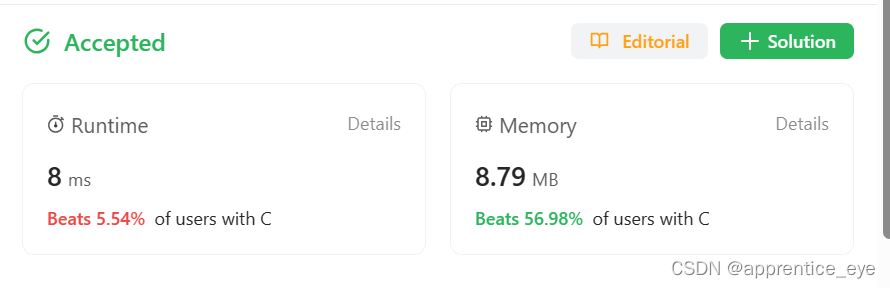
运行结果如图

108. Convert Sorted Array to Binary Search(将有序数组转换为二叉搜索树)

将有序数组转换为二叉搜索树，二叉搜索树可以将查找一个元素的时间复杂度从$O(n)$降到$O(lo{g}_{2}n)$，对于有二叉搜索树有这样一个特点对于树左子树的结点都小于根结点，树右子树上的结点都大于根结点，显然这也是递归定义，而且这种树的结构是不是很符合二叉搜素，所以在创建二叉搜索树的时候我们需要用到二分查找的算法，将整个数组的整个界限不断的二分，直到剩下一个元素，这是终止条件。
有了上面的这种说法所以我们就能写出下面的代码：

void createBinarySearchTree(int *nums, int left, int right, struct TreeNode* root){
     int middle = (left+right)/2;
     root->val = nums[middle];
     if(left<middle){
         root->left = (struct TreeNode *)malloc(sizeof(struct TreeNode));
         createBinarySearchTree(nums, left, middle-1, root->left);
     }else{
         root->left = NULL;
     }
    if(middle<right){
         root->right = (struct TreeNode *)malloc(sizeof(struct TreeNode));
         createBinarySearchTree(nums, middle+1, right, root->right);
    }else{
         root->right = NULL;
    }   
 }
struct TreeNode* sortedArrayToBST(int* nums, int numsSize) {
    struct TreeNode * root = (struct TreeNode *)malloc(sizeof(struct TreeNode));
    createBinarySearchTree(nums, 0, numsSize-1, root);
    return root;
}

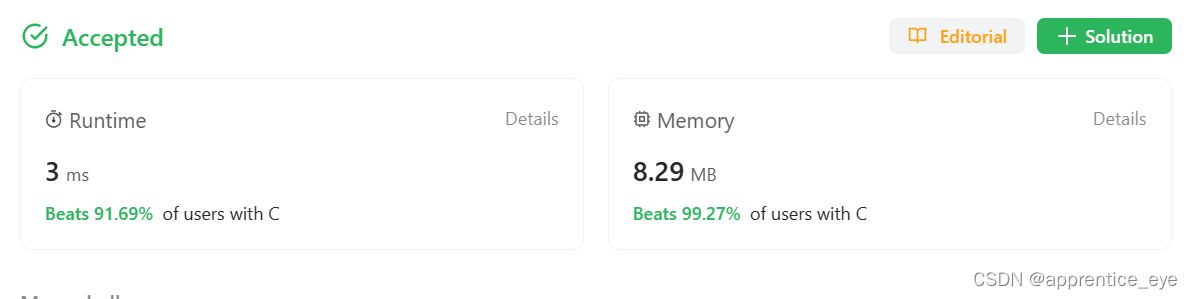
运行结果：