[HOT 100] 0051. N 皇后

1. 题目链接

51. N 皇后 - 力扣（LeetCode）

2. 题目描述

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

3. 题目示例

示例 1 :

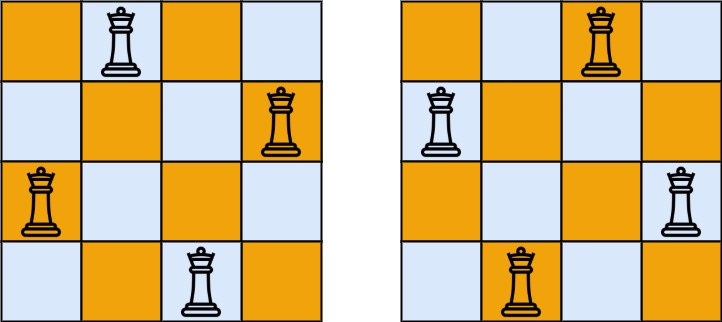
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2 :

输入：n = 1
输出：[["Q"]]

4. 解题思路

N皇后问题：在n×n的棋盘上放置n个皇后，使其互不攻击。每个皇后所在行、列、主对角线和副对角线均不能有其他皇后。使用回溯算法逐行放置皇后，通过标记数组快速判断冲突。

关键步骤：

1. 行处理：每行放置一个皇后，避免行冲突。
2. 列冲突：使用col数组标记已占用的列。
3. 对角线冲突：
   • 主对角线（左上→右下）：r - c为定值，索引转换为r - c + n - 1。
   • 副对角线（右上→左下）：r + c为定值，直接作为索引。
4. 回溯过程：尝试当前行的所有列，若合法则递归处理下一行，否则回溯。

5. 题解代码

class Solution {
    public List<List<String>> solveNQueens(int n) {
        List<List<String>> ans = new ArrayList<>(); // 存储所有解
        int[] queens = new int[n]; // queens[r]表示第r行皇后所在的列
        boolean[] col = new boolean[n]; // 标记列是否被占用
        boolean[] diag1 = new boolean[2 * n - 1]; // 主对角线（左上到右下）
        boolean[] diag2 = new boolean[2 * n - 1]; // 副对角线（右上到左下）
        dfs(0, queens, col, diag1, diag2, ans); // 从第0行开始递归
        return ans;
    }

    private void dfs(int r, int[] queens, boolean[] col, boolean[] diag1, boolean[] diag2, List<List<String>> ans) {
        int n = col.length;
        if (r == n) { // 所有行处理完毕，生成棋盘
            List<String> board = new ArrayList<>(n);
            for (int c : queens) {
                char[] row = new char[n];
                Arrays.fill(row, '.'); // 初始化全为.
                row[c] = 'Q'; // 在皇后位置放置Q
                board.add(new String(row));
            }
            ans.add(board);
            return;
        }

        for (int c = 0; c < n; c++) { // 尝试当前行的每一列
            int d1 = r - c + n - 1; // 主对角线索引
            int d2 = r + c; // 副对角线索引
            if (!col[c] && !diag1[d1] && !diag2[d2]) { // 当前位置合法
                queens[r] = c; // 记录皇后位置
                col[c] = diag1[d1] = diag2[d2] = true; // 标记占用
                dfs(r + 1, queens, col, diag1, diag2, ans); // 处理下一行
                col[c] = diag1[d1] = diag2[d2] = false; // 回溯，解除标记
            }
        }
    }
}

6. 复杂度分析

• 时间复杂度：O(n!)
  最坏情况下需要遍历所有可能的放置方式，但由于剪枝（冲突检测），实际复杂度远小于O(n!)。
• 空间复杂度：O(n^2)
  递归栈深度为O(n)，标记数组和中间结果占O(n)空间。生成的结果包含O(n!)个解，每个解占用O(n^2)空间（不计入复杂度分析）。