简单的线性回归

import numpy as np
import matplotlib.pyplot as plt

# X 表示训练数据的特征, 即披萨的直径
X = np.array([[6], [8], [10], [14], [18]])
# X = np.array([6, 8, 10, 14, 18])
# 让X变成只有一列, 行数不知道多少(-1表示)
# X = X.reshape(-1, 1)

# y 表示披萨价格的向量
y = [7, 9, 13, 17.5, 18]

plt.figure()
plt.title("Pizza price plotted against diameter")
plt.xlabel("Diameter in inches")
plt.ylabel("Price in dollars")
# x轴数据，y轴数据，format_string控制曲线的格式字串
# format_string 由颜色字符，风格字符(省略)，和标记字符
plt.plot(X, y, "k.")
plt.axis([0, 25, 0, 25])
plt.grid(True)
plt.show()

代码结果：

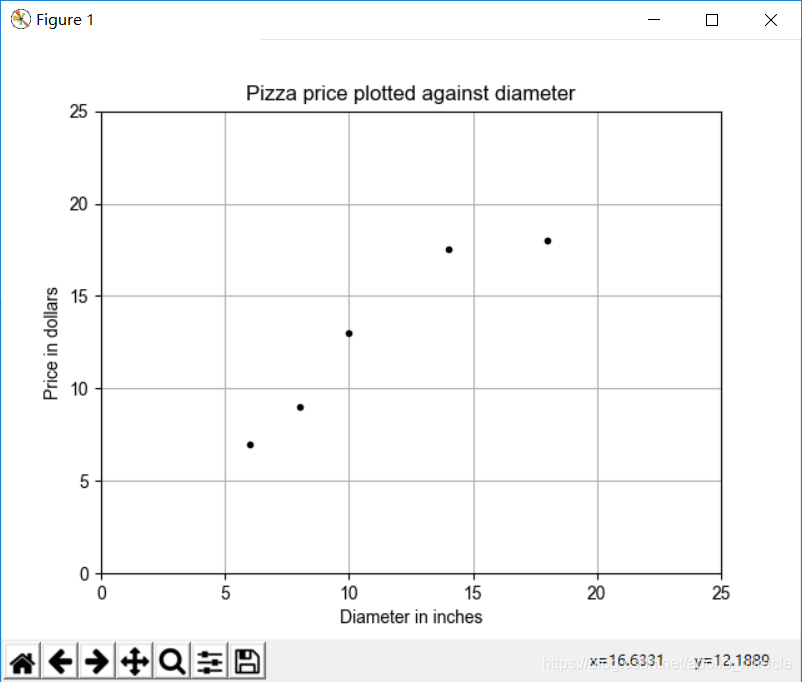
import numpy as np
# 线性回归
from sklearn.linear_model import LinearRegression

# X 表示训练数据的特征, 即披萨的直径
X = np.array([[6], [8], [10], [14], [18]])

# y 表示披萨价格的向量
y = [7, 9, 13, 17.5, 18]

# 创建一个估计器实例
model = LinearRegression()
# 用训练数据拟合模型
model.fit(X, y)
# 可以是一个列表(预测多个披萨)
test_pizza = np.array([[12]])
# 预测一个直径为12的披萨的价格(列表)
predicted_price = model.predict(test_pizza)[0]
print('A 12" pizza should cost: $%.2f' % predicted_price)

# 2.3计算残差平方和
residual = np.mean((model.predict(X) - y) ** 2)
print('Residual sum of squares: %.2f' % residual)

代码结果：

A 12" pizza should cost: $13.68
Residual sum of squares: 1.75

"""求方差"""
import numpy as np

# X 表示训练数据的特征, 即披萨的直径
X = np.array([[6], [8], [10], [14], [18]])

# 求x平均值
x_bar = X.mean()

# 求方差, 贝塞尔校正(样本数量减一)
variance = ((X - x_bar) ** 2).sum() / (X.shape[0] - 1)
# variance = np.sum((X - x_bar) ** 2) / (X.shape[0] - 1)
print(variance)

# 2.5使用numpy中的var的方法计算方差, 参数ddof可以设置贝塞尔校正
variance = np.var(X, ddof=1)
print(variance)

代码结果：

23.2
23.2

"""求协方差"""
import numpy as np

# X 表示训练数据的特征, 即披萨的直径
X = np.array([[6], [8], [10], [14], [18]])

# y 表示披萨价格的向量
y = np.array([7, 9, 13, 17.5, 18])

# 求x平均值
x_bar = X.mean()

# 求y平均值
y_bar = y.mean()

# 求协方差
covariance = np.multiply((X - x_bar).transpose(), y - y_bar).sum() / (X.shape[0] - 1)
# covariance = np.sum(np.multiply((X - x_bar).transpose(), y - y_bar)) / (X.shape[0] -1)
print(covariance)

# 使用numpy中的cov的方法计算协方差
variance = np.cov(X.transpose(), y)[0][1]
print(variance)

代码结果：

22.65
22.650000000000002

"""评价模型"""
import numpy as np
from sklearn.linear_model import LinearRegression

# X 表示训练数据的特征, 即披萨的直径
X_train = np.array([[6], [8], [10], [14], [18]])
# y 表示披萨价格的向量
y_train = [7, 9, 13, 17.5, 18]

# X 表示测试数据的特征, 即披萨的直径
X_test = np.array([[8], [9], [11], [16], [12]])
# y 表示披萨价格的向量
y_test = [11, 8.5, 15, 18, 11]

model = LinearRegression()
model.fit(X_train, y_train)
# LinearRegression类的score方法返回模型的R方值
r_squared = model.score(X_test, y_test)
print(r_squared)

代码结果：

0.6620052929422553