数据驱动的动态分析3：Dynamic Mode Decomposition(DMD)

@[TOC](lecture3-Dynamic Mode Decomposition(DMD))

纯新手！纯个人理解，主要拿来应用时间序列分析，没有数学基础，自用，勿喷。
lecture1介绍了SVD，lecture2介绍了POD，很重要，但是没做整理，略。

研究问题

在一个线性系统里，如何对未来数据进行预测？

公式

lecture里只介绍了 SVD-based DMD:

1. 数据准备

将时间序列数据矩阵 $V_1^N$ 拆分为两个矩阵：
$$V_1^{N-1}=[v_1,v_2,\dots ,v_{N-1}]$$
$$V_2^N=[v_2,v_3,\dots ,v_N]$$
其中 $v_k\in {\mathbb{R}}^n$ 表示第 $k$ 个时间点的状态快照,$V_1^N\in {\mathbb{R}}^{M\times N}$是一个数据矩阵，，其列代表各个快照。这些快照被假设通过线性映射相互关联，该线性映射定义了一个线性动力系统：
$$v_{i+1}=A{v}_i$$

以矩阵形式表示：
$$V_2^N=A{V}_1^{N-1}+r{e}_{N-1}^T,$$
The SVD-based approach yields the matrix $\tilde{S}$ that is related to $A$ via a similarity transform.

---

2. 奇异值分解 (SVD)

对 $V_1^{N-1}$ 进行奇异值分解：
$$V_1^{N-1}=U\Sigma W^T$$

• $U\in {\mathbb{R}}^{n\times r}$：左奇异向量矩阵（POD，正交分解模式），满足 $U^{T}U=I_r$
  POD的核心：找到最优正交基 $U$
• $\Sigma \in {\mathbb{R}}^{r\times r}$：奇异值对角矩阵
• $W\in {\mathbb{R}}^{(N-1)\times r}$：右奇异向量矩阵，满足 $W^{T}W=I_r$
• $r$：保留的奇异值个数（可根据能量准则截断）

---

3. 构建降阶矩阵

计算降阶矩阵：

$$\tilde{S}=U^T{V}_2^{N}W{\Sigma }^{-1}$$
其中 $\tilde{S}\in {\mathbb{R}}^{r\times r}$ 是原系统矩阵 $A$ 在 POD 子空间上的投影。

构建推导：

$$V_2^N=A{V}_1^{N-1}+r{e}_{N-1}^T$$

• $re$：残差

假设条件

1. $r$ 与 $U$ 正交，即 $U^{T}r=0$
2. $V_2^N$ 的列在 $U$ 的列张成的空间 Column Space中（POD 假设），即 $V_2^N=UC$ 对某个 $C$ 成立
   Column space: 该矩阵的所有列向量通过线性组合所能得到的所有向量的集合。这句话意味着：下一个时刻的任何一个状态（即 $V_2^N$ 的任意一列），都可以完全由过去时刻的主导模式 $U$ 的线性组合来表示。

推导过程

由已知条件：
$$V_2^N=AU\Sigma W^T+r{e}_{N-1}^T$$

两边左乘 $U^T$：
$$U^T{V}_2^N=U^{T}AU\Sigma W^T+U^{T}r{e}_{N-1}^T$$

利用正交性假设 $U^{T}r=0$：
$$U^T{V}_2^N=U^{T}AU\Sigma W^T$$

整理得到：
$$U^{T}AU=(U^T{V}_2^N)W{\Sigma }^{-1}\equiv \tilde{S}$$
于是得到降价矩阵（Reduced-Order Model, ROM）：
$$\tilde{S}=U^T{V}_2^{N}W{\Sigma }^{-1}$$

---

4. 特征分解

对 $\tilde{S}$ 进行特征分解：
$$\tilde{S}{y}_i={\lambda }_i{y}_i$$

• ${\lambda }_i$：第 $i$ 个 DMD 特征值
• $y_i$：$\tilde{S}$ 的第 $i$ 个特征向量

这里A和$\tilde{S}$做的是合同变换（维基百科说是相似变换相关），$\tilde{S}$的特征值近似A的特征值，如果y是$\tilde{S}$的特征向量，则$Uy$近似A的特征向量。

• 当 $U$ 是方阵且正交时（即保留所有POD模式，$r=n$），$\tilde{S}=U^{T}AU$ 是相似变换，特征值精确相同
• 当 $U$ 是瘦正交矩阵时（$r<n$，降阶情况），$\tilde{S}$ 是 $A$ 在子空间上的投影，特征值是 $A$ 的 $r$ 个主导特征值的近似

---

5. 重构 DMD 模式

将降阶特征向量映射回原始状态空间：
$${\varphi }_i=U{y}_i$$
其中

• ${\varphi }_i\in {\mathbb{R}}^n$ 是第 $i$ 个 DMD 模式（A的近似特征向量）。
• $U\in {\mathbb{R}}^{n\times r}$，用来project back to high dimensional space (from coordinate to vector)
• $y_i\in {\mathbb{R}}^r$, low dimension coordinate

---

6. 结果（deepseek说的）

• DMD 特征值：${\lambda }_i$ 描述模式的动态行为（增长/衰减率和频率）
• DMD 模式：${\varphi }_i$ 表示在状态空间中的相干空间结构

通过 DMD 分解，原系统动态可近似为：
$$v(t)\approx \sum _{i=1}^r{\varphi }_i{\lambda }_i^{t/\Delta t}{b}_i$$
其中 $b_i$ 是初始幅值，可通过初始条件 $v_1$ 在 DMD 模式上的投影求得。

仿真

数据描述

generate data from numerical integration of a partial differential equation
非线性薛定谔方程：

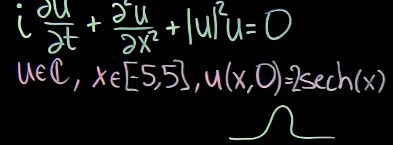
initial situation:

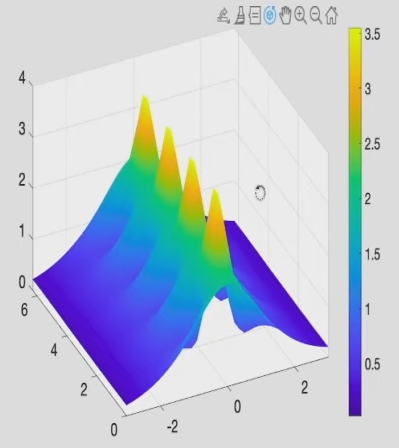
一开始是S曲线，随着时间推移，lt localizes and bunches up （局部化并聚集起来，黄色尖峰），然后breath out, and thenm sucks in.
过程：

1. seed dyamic mode decomposition
2. create data matrics (complex matrics)：each column of X is advanced by one time step when you look at the same column of Y
   
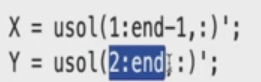
3. 计算DMD
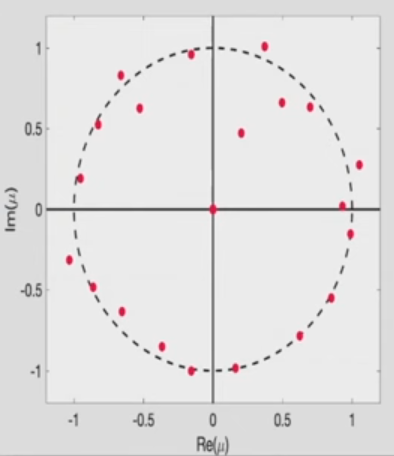
4. 在复平面绘制：横轴实轴，纵轴虚轴。描述：0附近有很多eigen values，只有20个非零的eigen values.（非零数量是A较小维度的数量）
   

如果能量是守恒的，在每个时间点对复数解进行空间积分 =0 不随时间变化，说明系统上的粒子数量守恒：
$${\int }_{-5}^5|u(x,t){|}^{2}dx$$

unitary matrix 酉矩阵 这个方法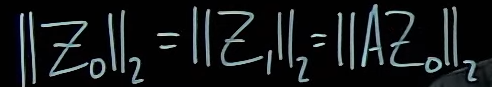

unitary prediction 可以预测更长的时间，牺牲了部分准确性(short-term accuracy)。从长远来看，解决方案保持有界(bounded error)且相对接近。（regular DMD方法在更长的时间尺度误差会很大）

参考

https://www.youtube.com/watch?v=w-CjCteRPuU
deepseek帮助理解 https://chat.deepseek.com/
维基百科 借鉴公式 https://en.wikipedia.org/wiki/Dynamic_mode_decomposition