从度量张量、相关系数生成椭圆参数

原创已于 2025-05-20 13:24:08 修改 · 1.2k 阅读

26 ·

CC 4.0 BY-SA版权

文章标签：

#线性代数 #矩阵 #几何学 #数据可视化

于 2024-11-01 11:51:47 首次发布

度量张量、高斯随机变量相关系数都可以用椭圆来进行可视化，下面讲一下两者的本质和联系，以及绘制椭圆可视化过程中的常见问题。都以二维平面的椭圆为例。

度量张量

又叫黎曼度量，物理学译为度规张量，是指一用来衡量度量空间中距离，面积及角度的二阶张量。 $x_i$ 为欧几里得空间中一点的坐标，在其构成的局部坐标系统中，对 $x_i$ 附近（切空间）的的点有 $x=x_i+dx$ ，度量张量可记为 $G(x_i)$ ，满足
$ds^2 = dx^T G(x_i )dx$ 如果对这个度量张量进行可视化，可以用 $dx^T G(x_i) dx = 1$ 的椭圆来绘制。
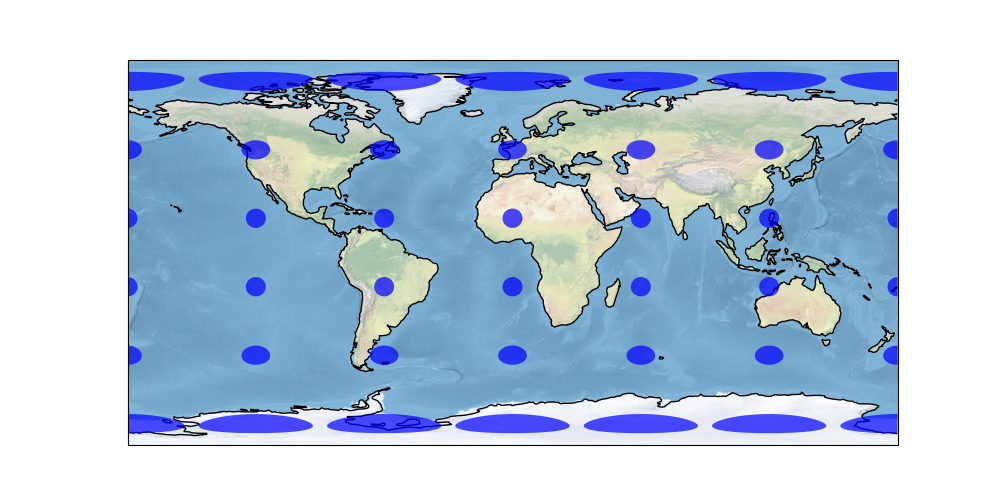
在这里插入图片描述

一个典型的黎曼空间中度量张量的椭圆可视化，其中不同位置的张量有显著差别
图1. 两个典型的黎曼空间中度量张量的椭圆可视化，其中不同位置的张量有显著差别地球图片源自[1]

椭圆参数

通常用方程 $x^TGx=1$ 表示一个椭圆，所以G中就包含了全部所需参数。然而，很多画椭圆函数（例如python中plt.patch.Ellipse）提供的参数是长轴长、短轴长和逆时针长轴旋转角度。如何从 $G$ 解析这些参数是一个关键问题。
示意椭圆

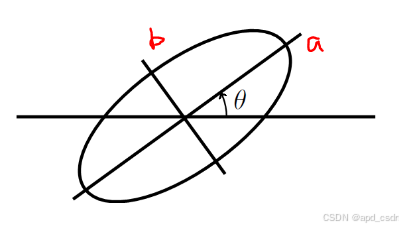
考虑二维平面上的椭圆，有长半轴长度 $a$ ，短半轴长度 $b$ ，逆时针逆时针长轴旋转角度 $\theta$ . 对于 $\theta = 0$ 的普通椭圆，容易写出
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
对应的 $G$ 就是：
$\begin{bmatrix} \frac{1}{a^2} & 0 \\ 0 & \frac{1}{b^2} \end{bmatrix}$
可以直接从对角阵元素计算得到长短轴半轴长度。

然而，当旋转角度不为0时，我们考虑当前椭圆是由普通椭圆旋转而来的，旋转前的椭圆上某点坐标记为 $Y$ ，有
$Y=Q^TX$
其中 $Q^T$ 为
$\begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix}$

$Y$ 满足椭圆方程 $Y^T U Y=1$ ， $U=diag(\frac{1}{a^2},\frac{1}{b^2})$
进一步有 $X^TQUQ^TX=1$ ，所以可以得到 $G=QUQ^T$ . 对称矩阵 $G$ 分解得到这种形式，只需要做正交对角化就可以了（或调用SVD分解的函数）。最后，根据分解出的 $U$ 求 $a, b$ ，根据 $Q$ 求 $\theta$ .

但是，这里有个坑，分解出的矩阵 $Q$ 只保证了列向量的是特征向量、满足正交性。这样的向量有两种可能解： $(\cos \theta, \sin \theta)$ 和 $(-\cos \theta, -\sin \theta)$ 。所以，求解 $\theta$ 应该用 $\frac{q_{12}}{q_{11}})$ ，解出的 $\hat{\theta}=\theta+k\pi$ ，对椭圆而言旋转 $\pi$ 没有任何变化。

代码举例：从相关系数给出椭圆参数，可直接用于plt画椭圆

import numpy as np 
import matplotlib.pyplot as plt
import matplotlib.patches as patches

def sigma_to_abtheta(mat22):
    U,Sigma,V = np.linalg.svd(mat22,full_matrices=True)
    a = np.sqrt(Sigma[0])
    b = np.sqrt(Sigma[1])
    theta = np.arctan(U[0,1]/U[0,0]) # U = QT, row is feature vector
    return a,b,theta

mat22 = np.array([[ 0.00287626 -0.00084234]
 [-0.00084234  0.00604468]])
a,b,theta = sigma_to_abtheta(mat22)
ellipse_1 = patches.Ellipse((0.5,0.5),
                                 width=2*a, height=2*b, 
                                 facecolor='#00FF00', angle=theta/np.pi*180., 
                                 edgecolor='#00FF00', linewidth=1, fill=False)
fig,ax = plt.subplots()
ax.add_patch(ellipse_1)
plt.show()