openGL中向量的加减乘除运算

1.向量加法

LearnOpenGL - Transformations

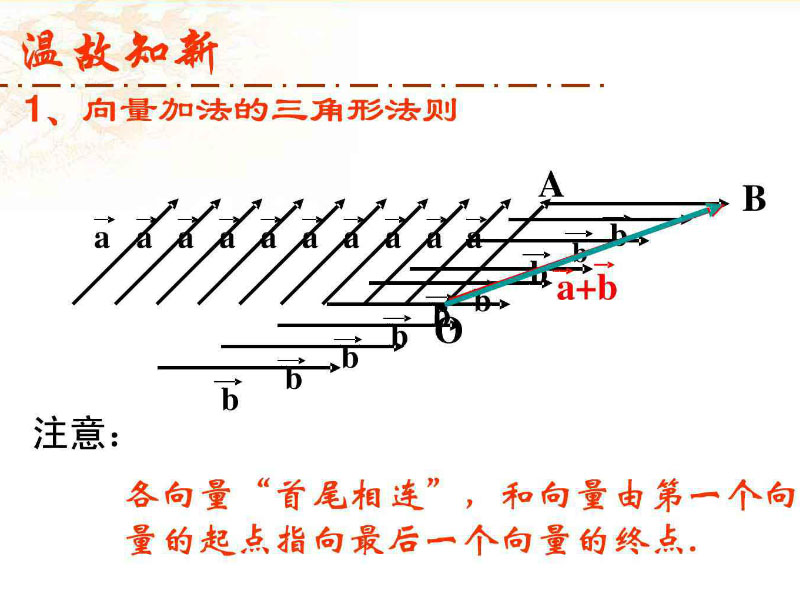
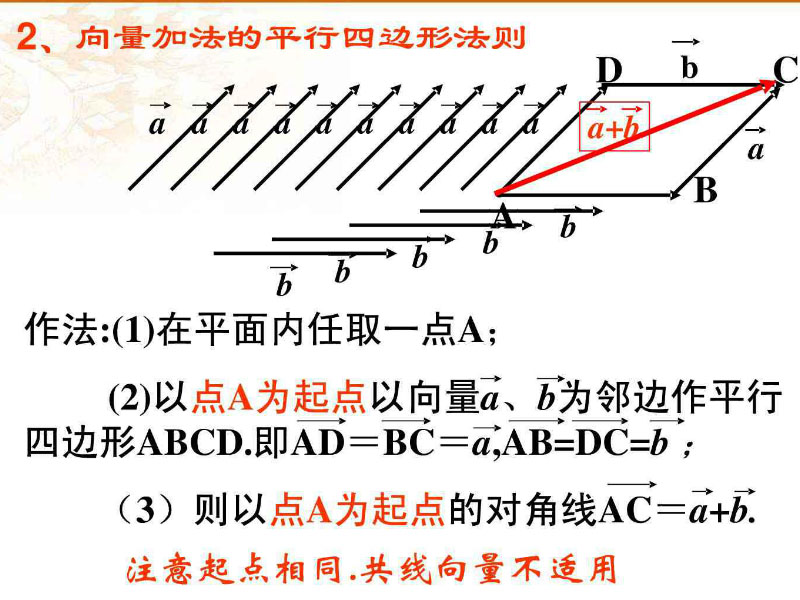
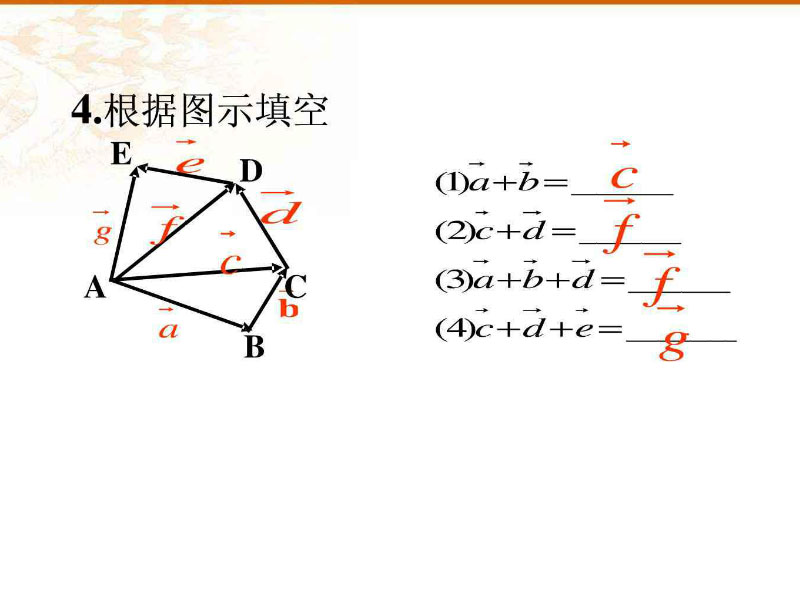
向量加法举栗子，使用LearnOpenGL书山的例子

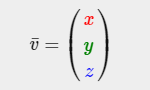
向量的加法

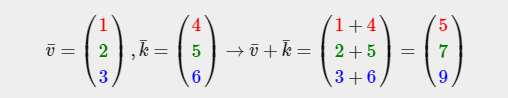
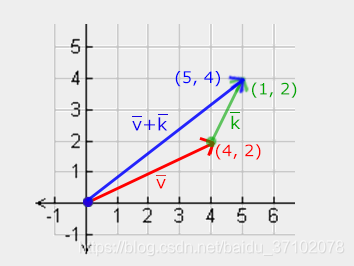
2.向量减法

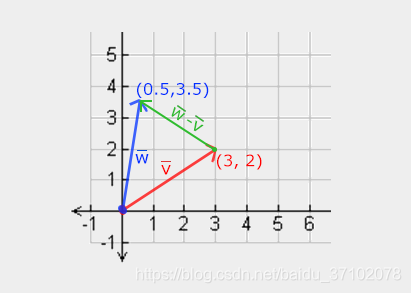
减法应该就是把方向反过来，做加法而已，

注意是b的终点到a的终点

向量减法举栗子，还使用LearnOpenGL书山的例子

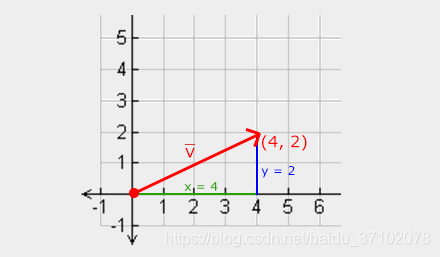
向量的长度

向量归一化(变成单位向量)

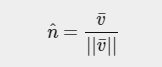
3.向量的点乘

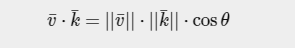如果2个都是单位向量时：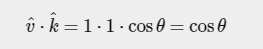

 

当角度为90度时，余弦或cos函数变为0，而当角度为0时，余弦或cos函数变为1。这使我们可以使用点积轻松地测试两个向量是正交还是平行（正交表示 向量彼此成直角）。

如下是2个单位向量的点积计算： cosθ=-0.8,可计算出角度为θ=143.1°    请看这：反正弦、反余弦和反正切 (shuxuele.com)

 

点乘的几何意义是可以用来表征或计算两个向量之间的夹角，以及在b向量在a向量方向上的投影，

4.向量的叉乘

叉积仅在3D空间中定义，并采用两个非平行向量作为输入，并产生与两个输入向量正交的第三向量

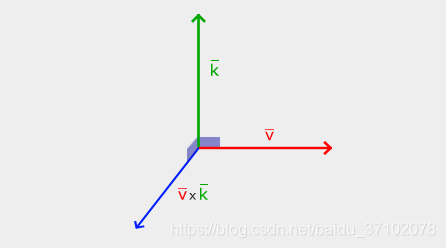
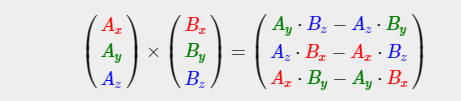
叉乘的几何意义：在三维几何中，向量a和向量b的叉乘结果是一个向量，更为熟知的叫法是法向量，该向量垂直于a和b向量构成的平面。

 

5.向量除法

我们先来看看什么是除法——已知两个因数的积与其中一个因数，求另一个因数的运算，叫做除法。除法可以看成是“乘法的逆运算”．

所以，简单的说，逆运算就是在求逆元。

而我们知道的向量的乘法有两种，一个是数量积数量积(点乘)，一个是向量积向量积（叉乘）。

·先来看看数量积有没有逆运算呢？
如果数量积有除法的话，设向量和的乘积为(数)，即那么

如果数量积有除法的话，设向量a和b的乘积为x(数)，即a.b=x 那么x/a=b由数量积的定义，
两个向量的数量积等于一个向量的模乘以另一个向量在此向量上的投影，那么如果a确定的话，
改变b的方向和大小，发现有无数个向量的投影等用于b在a方向上的投影，即如果乘积不变，
则向量b的解是无穷多的，所以向量的商不是唯一确定的。所以数量积的逆运算是没有的╮(╯_╰)╭大概看图就这样理解吧……

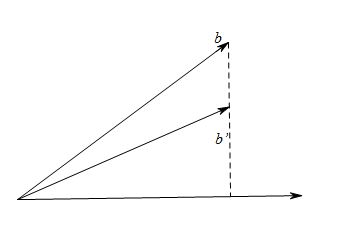
对于高中的小朋友讲完数量积其实就可以差不多告一段落了~

但是还有向量积呢……

那再来看看向量积有没有逆运算呢？我也继续假设向量积存在除法，因为向量积的结果仍然是一个向量，
设向量a和b的乘积为x(向量)，即a*b=x那么x/a=b我们知道，向量积的模可以看作平行四边形的面积，那么如果a确定的话，
那么变化x的长度和方向，也可以得到相同面积的平行四边形，显然向量b的解是无穷多的，
所以向量的商不是唯一确定的。所以数量积的逆运算还是没有的╮(╯_╰)╭

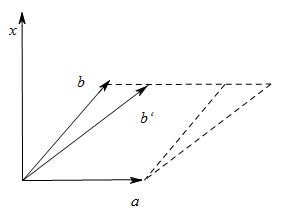
我们发现对于数量积和向量积，他们的逆运算都是不确定的，所以，向量的除法是不存在的.

 

其实学了群以后，就不用这么繁琐的讲这么多了。