TOYS POJ 2318 计算几何 叉乘的应用

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 15060		Accepted: 7270

Description

Calculate the number of toys that land in each bin of a partitioned toy box. 
Mom and dad have a problem - their child John never puts his toys away when he is finished playing with them. They gave John a rectangular box to put his toys in, but John is rebellious and obeys his parents by simply throwing his toys into the box. All the toys get mixed up, and it is impossible for John to find his favorite toys. 

John's parents came up with the following idea. They put cardboard partitions into the box. Even if John keeps throwing his toys into the box, at least toys that get thrown into different bins stay separated. The following diagram shows a top view of an example toy box. 
 
For this problem, you are asked to determine how many toys fall into each partition as John throws them into the toy box.

Input

The input file contains one or more problems. The first line of a problem consists of six integers, n m x1 y1 x2 y2. The number of cardboard partitions is n (0 < n <= 5000) and the number of toys is m (0 < m <= 5000). The coordinates of the upper-left corner and the lower-right corner of the box are (x1,y1) and (x2,y2), respectively. The following n lines contain two integers per line, Ui Li, indicating that the ends of the i-th cardboard partition is at the coordinates (Ui,y1) and (Li,y2). You may assume that the cardboard partitions do not intersect each other and that they are specified in sorted order from left to right. The next m lines contain two integers per line, Xj Yj specifying where the j-th toy has landed in the box. The order of the toy locations is random. You may assume that no toy will land exactly on a cardboard partition or outside the boundary of the box. The input is terminated by a line consisting of a single 0.

Output

The output for each problem will be one line for each separate bin in the toy box. For each bin, print its bin number, followed by a colon and one space, followed by the number of toys thrown into that bin. Bins are numbered from 0 (the leftmost bin) to n (the rightmost bin). Separate the output of different problems by a single blank line.

Sample Input

5 6 0 10 60 0
3 1
4 3
6 8
10 10
15 30
1 5
2 1
2 8
5 5
40 10
7 9
4 10 0 10 100 0
20 20
40 40
60 60
80 80
 5 10
15 10
25 10
35 10
45 10
55 10
65 10
75 10
85 10
95 10
0

Sample Output

0: 2
1: 1
2: 1
3: 1
4: 0
5: 1

0: 2
1: 2
2: 2
3: 2
4: 2

Hint

As the example illustrates, toys that fall on the boundary of the box are "in" the box.

Source

 

 

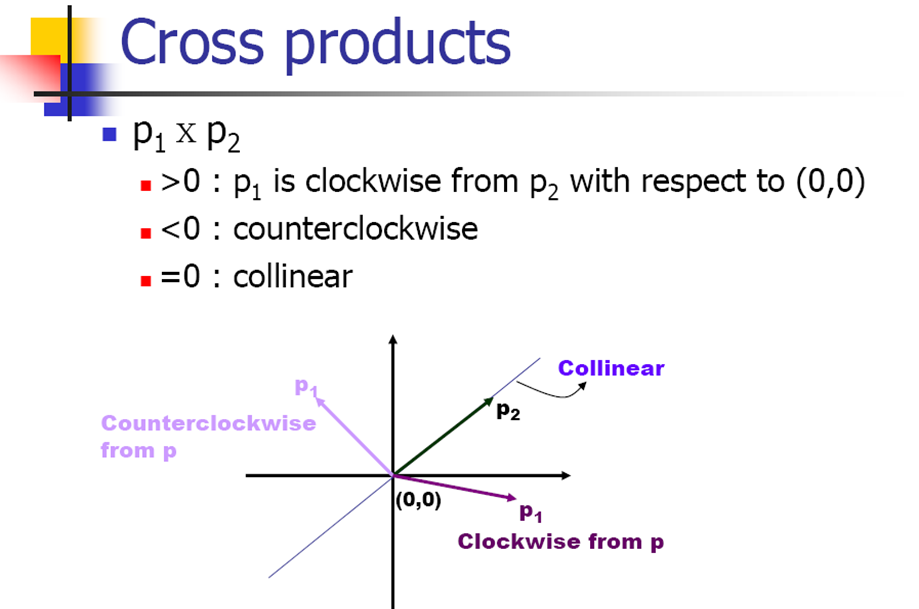
利用这个性质判断点在矩形中哪个区域内！

 

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<sstream>
#include<algorithm>
#include<queue>
#include<deque>
#include<iomanip>
#include<vector>
#include<cmath>
#include<map>
#include<stack>
#include<set>
#include<fstream>
#include<memory>
#include<list>
#include<string>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
#define MAXN 5003
#define N 21
#define MOD 1000000
#define INF 1000000009
#define eps 0.00000001
/*
已知p1Xp2 >0 说明p1 在 p2的顺时针方向
盒子中所有界限 按升序给出，只需从前到后按顺序判断（一个点到边界线上面的顶点）叉乘（边界线向量） > 0 ?
那么将该点放入对应的盒子中！
*/
struct Point
{
    double x, y;
    Point() {}
    Point(double _x, double _y)
    {
        x = _x, y = _y;
    }
    Point operator-(const Point& b)const
    {
        return Point(x - b.x, y - b.y);
    }
    double operator^(const Point& b)const
    {
        return x*b.y - y*b.x;
    }
}toy[MAXN];
struct Line
{
    Point beg, end;
}a[MAXN];
int n, m, cnt[MAXN];
Point p1, p2;//左上角 右下角
int main()
{
    bool f = false;
    while (scanf("%d", &n), n)
    {
        memset(cnt, 0, sizeof(cnt));
        if (!f)
            f = true;
        else
            printf("\n");
        scanf("%d%lf%lf%lf%lf", &m, &p1.x, &p1.y, &p2.x, &p2.y);
        for (int i = 0; i < n; i++)
        {
            scanf("%lf%lf", &a[i].beg.x, &a[i].end.x);
            a[i].beg.y = p1.y, a[i].end.y = p2.y;
        }
        for (int i = 0; i < m; i++)
        {
            scanf("%lf%lf", &toy[i].x, &toy[i].y);
            int j;
            for (j = 0; j < n; j++)
            {
                if (((toy[i] - a[j].beg) ^ (a[j].end - a[j].beg)) > 0)
                {
                    /*Point s = (toy[i] - a[j].beg),b = (a[j].end - a[j].beg);
                        cout <<":::::::"<< ((toy[i] - a[j].beg) ^ (a[j].end - a[j].beg)) << endl;*/
                    cnt[j]++;
                    break;
                }
            }
            if (j == n)
                cnt[n]++;
        }
        for (int i = 0; i <= n; i++)
        {
            printf("%d: %d\n", i, cnt[i]);
        }
        //printf("\n");
    }
    return 0;
}

 

转载于:https://www.cnblogs.com/joeylee97/p/6925589.html