背包问题描述:
将有限的几个物品放入一个能承受固定重量的背包中,求能背包中物品的最大重量
package cm.com.algorithm.knapsack;
import cm.com.algorithm.knapsack.compare.SortCompare;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* 背包问题-贪心算法实现
*
* 核心思想:
* 优先放置最有价值的,在这里也就是最重的,然后将剩余空间放置能放下在最重的,以此类推...
*
* @author Memorys.liu
* @date 2019-07-03 10:31
*/
public class KnapsackGreedy {
private static final Integer[] goods = new Integer[]{2,4,2,8,3};
private static final int weight = 9;
private static List<Integer> goodsPlaced = new ArrayList<>();
private static int goodsPlacedWeight = 0;
public static void main(String[] args) {
//降序排序
Arrays.sort(goods,new SortCompare());
//放置物品
place(goods);
//打印数组
System.out.println(goodsPlaced);
}
/**
* 将商品放置到背包中
* @param goods
*/
private static void place(Integer[] goods) {
int j = 0;
for (int i = 0; i < goods.length; i++) {
if (goods[i] <= weight - goodsPlacedWeight){
goodsPlaced.add(goods[i]);
goodsPlacedWeight += goods[i];
j++;
}
}
}
}
图解:
不过图解中用的是一个二维数组,上述代码中使用的是一个一维数组。
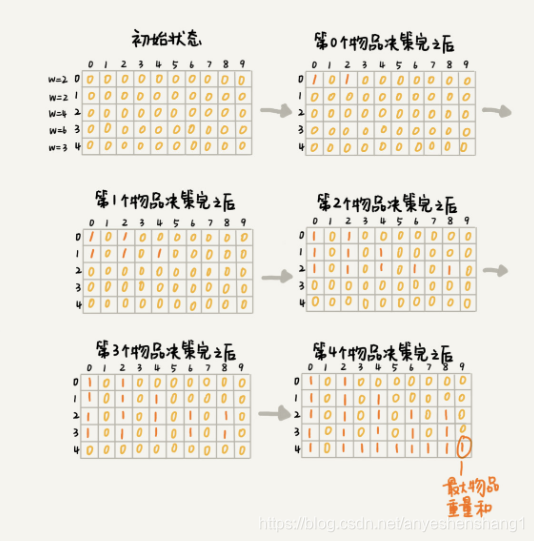










 本文深入探讨了背包问题的贪心算法实现,通过实例详细解释了如何在背包容量限制下,选择价值最大的物品组合,以达到最优解。代码示例清晰地展示了排序和物品放置的过程。
本文深入探讨了背包问题的贪心算法实现,通过实例详细解释了如何在背包容量限制下,选择价值最大的物品组合,以达到最优解。代码示例清晰地展示了排序和物品放置的过程。
















 7709
7709

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








