每日十题八股-2025年1月20日

最新推荐文章于 2025-12-05 17:02:52 发布

原创最新推荐文章于 2025-12-05 17:02:52 发布 · 551 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#java

八股背诵自用专栏收录该内容

66 篇文章

订阅专栏

1.LRU是什么？如何实现？
2.布隆过滤器怎么设计？时间复杂度？
3.说几个你懂的排序算法，并说明其时间空间复杂度
4.讲一下冒泡排序算法
5.讲一下快排原理
6.堆排序算法原理，稳定吗？
7.归并排序和快速排序的使用场景
8.什么是排序稳定性？
9.稳定和不稳定排序算法有什么特点？
10.说说快排流程，时间复杂度

排序算法参考

1.LRU是什么？如何实现？

缓存淘汰机制，优先淘汰最长时间未被访问的数据。
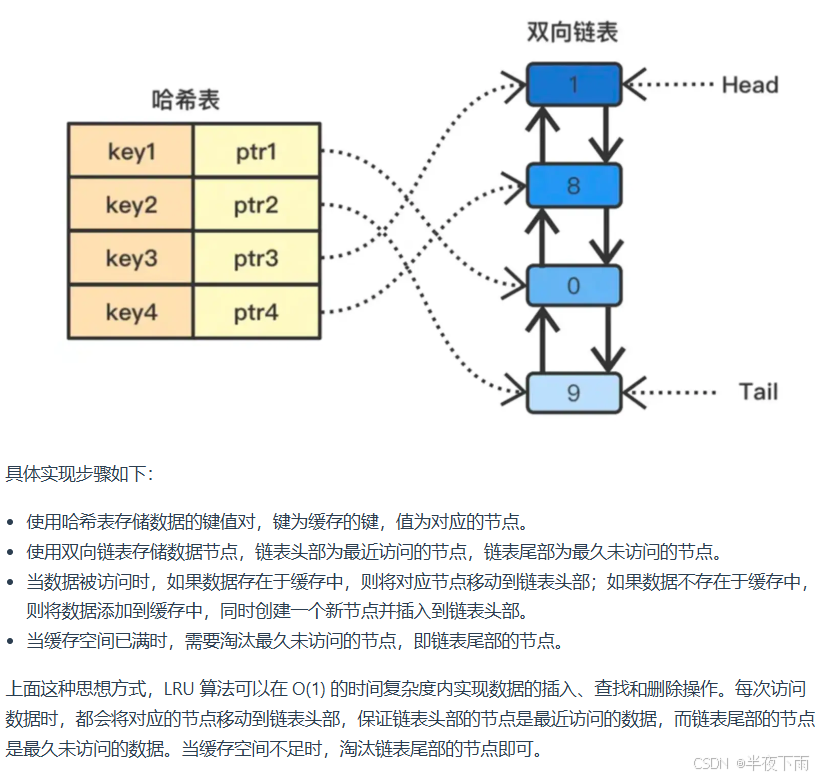
实现的方式是哈希表+双向链表结合。（力扣 hot 100 里面有实现题）。
实现的方式是哈希表+双向链表结合。链表头部为最近访问的节点，链表尾部为最久未访问的节点。哈希表的值就是双向链表中的对应节点。
在这里插入图片描述

2.布隆过滤器怎么设计？时间复杂度？

多个哈希函数，我们首先创建一个全由0组成的位数组（bit array)。
插入：每个哈希函数针对key计算出一个值，取模数组长度。然后分别把数组对应位置1。
查询数据库或缓存之前，先对key计算，判断布隆过滤器中是否对应位都为1，
不都为一那么就一定不存在。
O(k)的时间复杂度。k是哈希函数的个数。

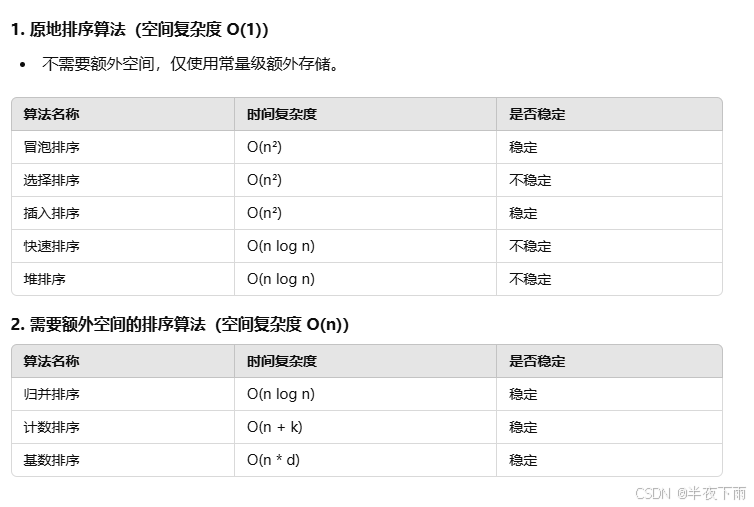
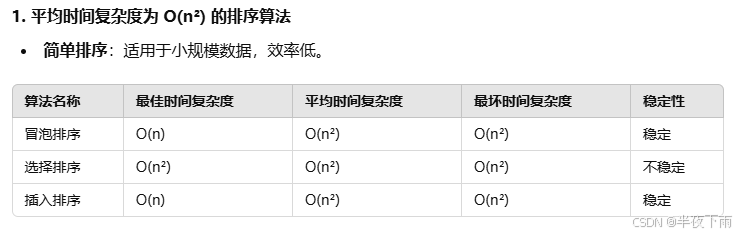
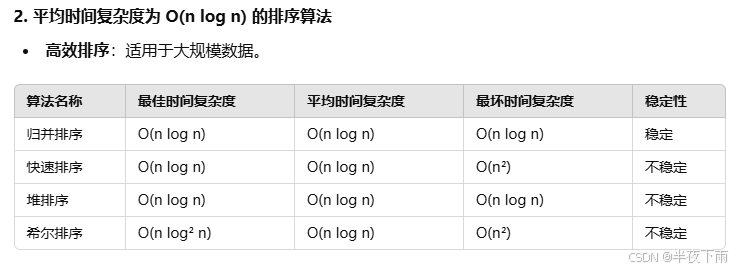
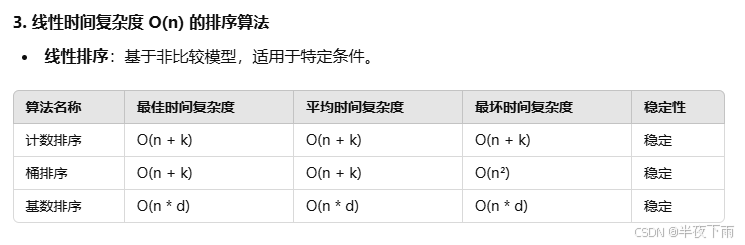
3.说几个你懂的排序算法，并说明其时间空间复杂度。

背第一个表。
在这里插入图片描述

O(n^2)
在这里插入图片描述

4.讲一下冒泡排序算法

冒泡排序得到一个升序数组的话，就是通过相邻元素的比较和交换，每次将最大的元素逐步“冒泡”到最后。最好时间复杂度是O(n)，平均是O(n^2），属于原地排序算法，并且稳定。

//降序
public static void BubbleSort1(int [] arr){

   int temp;//临时变量
   boolean flag;//是否交换的标志
   for(int i=0; i<arr.length-1; i++){   //表示趟数，一共 arr.length-1 次

       // 每次遍历标志位都要先置为false，才能判断后面的元素是否发生了交换
       flag = false;
       
       for(int j=arr.length-1; j>i; j--){ //选出该趟排序的最大值往后移动

           if(arr[j] < arr[j-1]){
               temp = arr[j];
               arr[j] = arr[j-1];
               arr[j-1] = temp;
               flag = true;    //只要有发生了交换，flag就置为true
           }
       }
       // 判断标志位是否为false，如果为false，说明后面的元素已经有序，就直接return
       if(!flag) break;
   }
}

5.讲一下快排原理

关键点在于如何选基准。平均时间复杂度是O(nlogn)，属于原地排序，不稳定。
在这里插入图片描述

public static void quickSort(int a[],int l,int r){
     if(l>=r)
       return;

     int i = l; int j = r; int key = a[l];//选择第一个数为key

     while(i<j){

         while(i<j && a[j]>=key)//从右向左找第一个小于key的值
             j--;
         if(i<j){
             a[i] = a[j];
             i++;
         }

         while(i<j && a[i]<key)//从左向右找第一个大于key的值
             i++;

         if(i<j){
             a[j] = a[i];
             j--;
         }
     }
     //i == j
     a[i] = key;
     quickSort(a, l, i-1);//递归调用
     quickSort(a, i+1, r);//递归调用
 }

6.堆排序算法原理，稳定吗？

完全二叉树（非满二叉树），节点必须（大于或小于）其子节点。
整个堆排序的过程中，只需要个别的临时存储空间，所以堆排序是原地排序算法。
堆排序包括建堆和排序两个操作，建堆的时间复杂度是O(n)，排序过程时间复杂度是O(nlogN)。所以，堆排序的整个时间复杂度是O(nlogN)。堆排序不是稳定的排序算法。
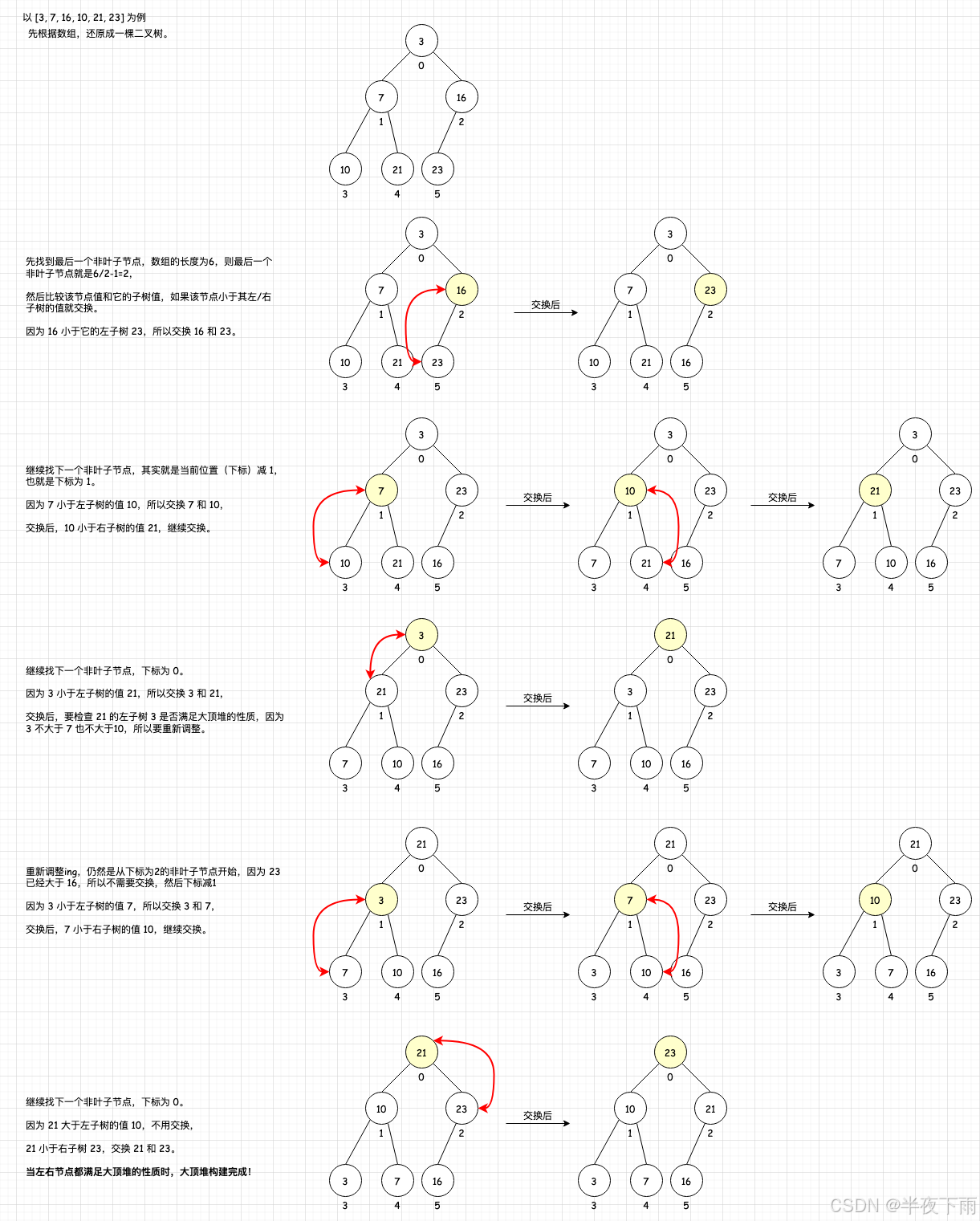
构建过程

public class HeapSort {
    
    // 主方法：测试堆排序
    public static void main(String[] args) {
        int[] arr = {4, 10, 3, 5, 1, 15, 7};
        heapSort(arr);
        System.out.println("排序后的数组：");
        for (int num : arr) {
            System.out.print(num + " ");
        }
    }

    // 堆排序主方法
    public static void heapSort(int[] arr) {
        int n = arr.length;

        // 1. 构建初始大顶堆
        for (int i = n / 2 - 1; i >= 0; i--) {
            heapify(arr, n, i);
        }

        // 2. 逐个交换堆顶元素到末尾，并重新调整堆
        for (int i = n - 1; i > 0; i--) {
            // 交换堆顶（最大值）和末尾元素
            swap(arr, 0, i);
            // 调整剩余部分为大顶堆
            heapify(arr, i, 0);
        }
    }

    // 调整堆，维护大顶堆性质
    public static void heapify(int[] arr, int n, int i) {
        int largest = i;  // 假设当前节点为最大值
        int left = 2 * i + 1;  // 左子节点索引
        int right = 2 * i + 2;  // 右子节点索引

        // 比较当前节点与左子节点
        if (left < n && arr[left] > arr[largest]) {
            largest = left;
        }

        // 比较当前最大节点与右子节点
        if (right < n && arr[right] > arr[largest]) {
            largest = right;
        }

        // 如果最大值发生改变，则交换，并递归调整
        if (largest != i) {
            swap(arr, i, largest);
            heapify(arr, n, largest);  // 递归调整子树
        }
    }

    // 交换数组中的两个元素
    public static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}