以前的学习笔记-PPO强化学习中的广义优势估计（GAE）

因为组里的服务器g了，故把以前的笔记搬上来

引言

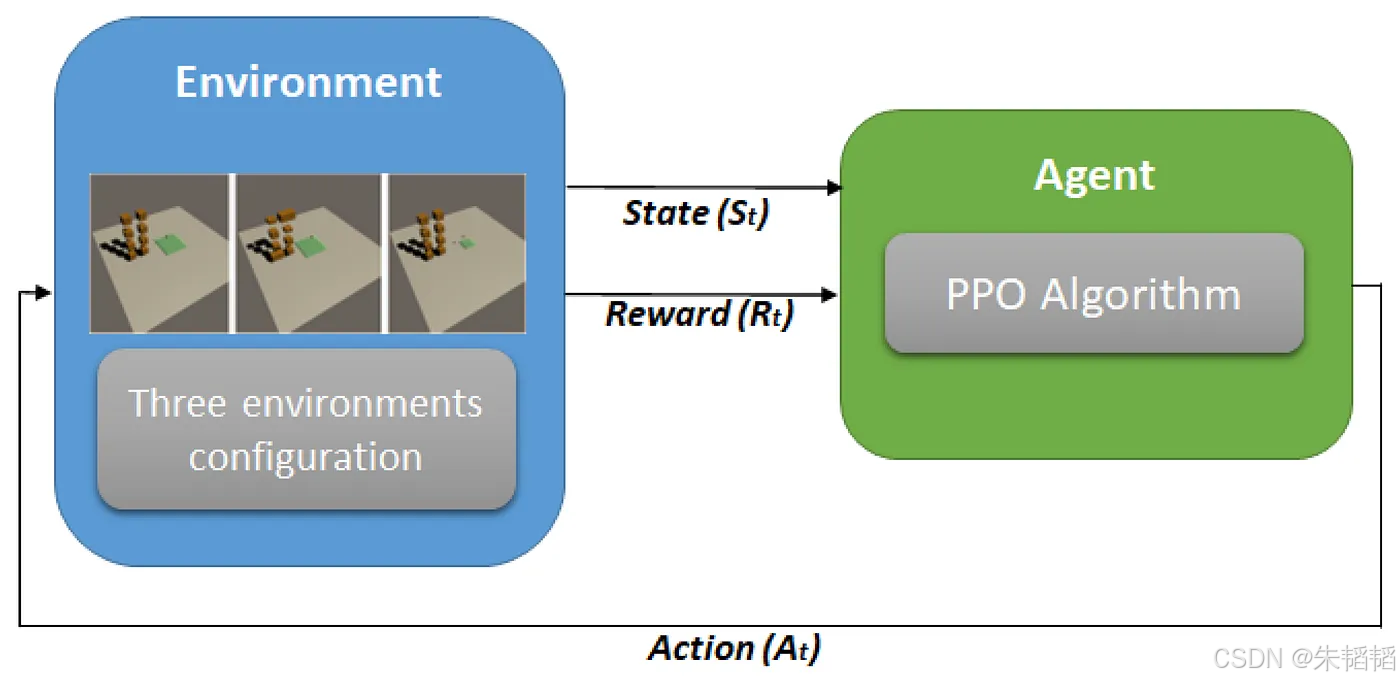
在强化学习领域，Proximal Policy Optimization (PPO) 算法以其稳定性、高效性和易于实现的特点，成为了解决复杂控制问题的主流方法。PPO 属于策略梯度方法，通过优化策略网络来指导智能体的决策过程。为了有效地训练策略网络，优势估计（Advantage Estimation）成为了一个关键环节。广义优势估计（Generalized Advantage Estimation, GAE）是用于提升 PPO 性能的优势估计技术，它通过平衡偏差和方差(实际上就是单步 TD 残差和蒙特卡洛方法的一个中间权衡)，从而更准确地评估策略的优劣。在LLM领域，GAE用于计算优势函数，从而更准确地评估生成文本，即当前LLM的Actor的优劣，是基线。

一、理论推导过程

1. 策略梯度定理与优势函数基础

PPO 的核心在于通过策略梯度定理优化策略参数 ，使得智能体能够可靠地达到最优解。策略梯度定理描述了如何通过策略的梯度来更新策略参数，从而最大化期望回报。其梯度形式可以表示为（参考的是这里）：

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[\sum _{t=0}^T{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)\cdot A^{\pi }(s_t,a_t)\right]$$

这里，${\pi }_{\theta }(a_t|s_t)$ 表示在状态 $s_t$ 下采取动作 a t a_t