文章目录
1 顺序存储二叉树的概念
从数据存储来看,数组存储方式和树的存储方式可以相互转换,即数组可以转换成树,树也可以转换成数组,看右面的示意图。
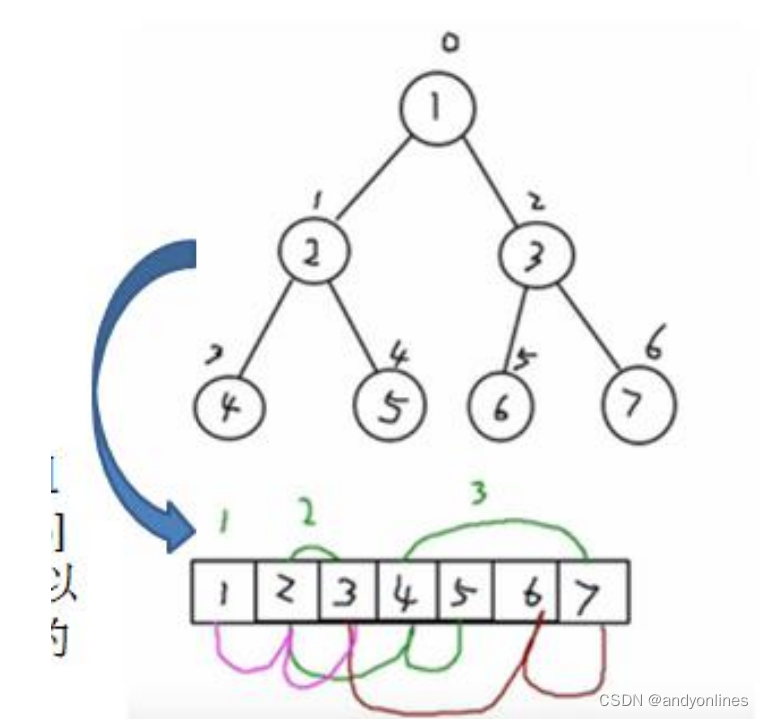
要求:
1) 右图的二叉树的结点,要求以数组的方式来存放 arr : [1, 2, 3, 4, 5, 6, 6]
2) 要求在遍历数组 arr 时,仍然可以以前序遍历,中序遍历和后序遍历的方式完成结点的遍历
顺序存储二叉树的特点:
1) 顺序二叉树通常只考虑完全二叉树
2) 第 n 个元素的左子节点为 2 * n + 1
3) 第 n 个元素的右子节点为 2 * n + 2
4) 第 n 个元素的父节点为 (n-1) / 2
5) n : 表示二叉树中的第几个元素(按 0 开始编号如图所示)





 文章介绍了顺序存储二叉树的概念,强调这种存储方式主要应用于完全二叉树。数组arr[1,2,3,4,5,6,7]能表示特定的二叉树结构,其中第n个元素的左子节点是2*n+1,右子节点是2*n+2,父节点是(n-1)/2。文章还提到,通过这种方式,仍能实现前序、中序和后序遍历。
文章介绍了顺序存储二叉树的概念,强调这种存储方式主要应用于完全二叉树。数组arr[1,2,3,4,5,6,7]能表示特定的二叉树结构,其中第n个元素的左子节点是2*n+1,右子节点是2*n+2,父节点是(n-1)/2。文章还提到,通过这种方式,仍能实现前序、中序和后序遍历。
















 2028
2028

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








