3.18做题记录

最新推荐文章于 2023-03-15 22:52:59 发布

原创最新推荐文章于 2023-03-15 22:52:59 发布 · 143 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#每日记录

这篇博客探讨了欧拉函数在数论中的作用，以及如何构建和解决虚树问题。文章通过实例展示了如何计算质因子数和森林旅行中的最短路径，并介绍了用于优化这些问题的算法。此外，还提到了在数据结构和图论中处理复杂问题的策略，如最小生成树和区间限制的最短路径问题。

ybtoj913. 「欧拉函数」质因子数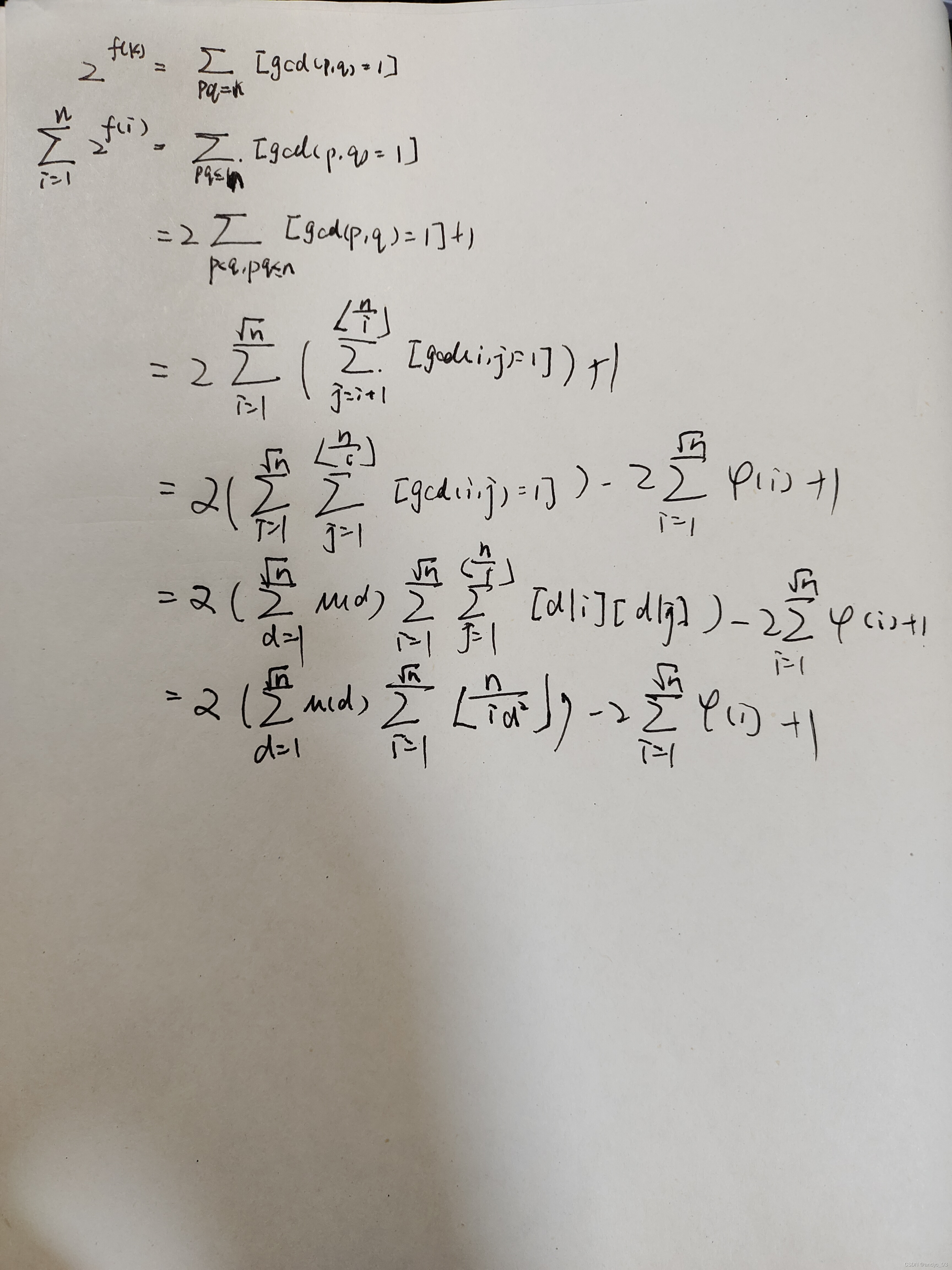

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e6+5;
const ll mod=1e9+7;
int phi[maxn],mu[maxn];
int is[maxn],pr[maxn],cnt;
ll n;
ll add(ll x,ll y)
{
    return (x+y)%mod;
}
void init()
{
    phi[1]=mu[1]=1;
    for(int i=2;i<maxn;i++)
    {
        if(!is[i])
        {
            pr[++cnt]=i;
            phi[i]=i-1;
            mu[i]=-1;
        }
        for(int j=1;j<=cnt && pr[j]*i<maxn;j++)
        {
            is[i*pr[j]]=1;
            if(i%pr[j]==0)
            {
                mu[i*pr[j]]=0;
                phi[i*pr[j]]=phi[i]*pr[j];
                break;
            }
            mu[i*pr[j]]=-mu[i];
            phi[i*pr[j]]=phi[i]*(pr[j]-1);
        }
    }
    for(int i=2;i<maxn;i++) phi[i]=add(phi[i],phi[i-1]);
}
ll solve(ll m)
{
    ll res=0;
    for(int d=1;d<=m;d++)
    {
        if(!mu[d]) continue;
        ll sum=0;
        for(int i=1;i<=m/d;i++)
        {
            ll tmp=n/(1ll*i*d*d);
            if(!tmp) break;
            sum=add(sum,tmp);
        }
        res=add(res,sum*mu[d]%mod+mod);
    }
    return 2*(res-phi[m]+mod)%mod+1;
}
int main()
{
    freopen("prime.in","r",stdin);
    freopen("prime.out","w",stdout);
    int T;
    scanf("%d",&T);
    init();
    // for(int i=2;i<=10;i++) printf("%d %d\n",mu[i],phi[i]);
    while(T--)
    {
        scanf("%lld",&n);
        printf("%lld\n",solve(sqrt(n))%mod);
    }
    return 0;
}

ybtoj721. 「虚树」森林旅行

原题好像出自牛客挑战赛35E
对于每个树建立关键点的虚树，边权改为原树上的距离
关键点指连了增加m条边的或者是有询问的点，然后跑单源最短路即可

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=3e5+5;
const ll inf=1e18;
typedef pair<int,int> PII;
typedef pair<ll,int> PLI;
#define mp make_pair
int n,m,q,bh;
vector <int> G[maxn];
vector <PII> T[maxn<<4];
int dep[maxn],siz[maxn],dfn[maxn],dfstime;
int fa[maxn][21],qs[maxn],qt[maxn];
void dfs(int u,int f)
{
    dep[u]=dep[f]+1; fa[u][0]=f;
    siz[u]=1; dfn[u]=++dfstime;
    for(int i=1;i<=20;i++) fa[u][i]=fa[fa[u][i-1]][i-1];
    for(auto to:G[u])
    {
        if(to==f) continue;
        dfs(to,u);
        siz[u]+=siz[to];
    }
}
int lca(int x,int y)
{
    if(dep[x]<dep[y]) std::swap(x,y);
    for(int i=20;i>=0;i--)
        if(dep[fa[x][i]]>=dep[y])
            x=fa[x][i];
    if(x==y) return x;
    for(int i=20;i>=0;i--)
        if(fa[x][i]!=fa[y][i])
            x=fa[x][i],y=fa[y][i];
    return fa[x][0];
}
bool cmp(int x,int y)
{
    return dfn[x]<dfn[y];
}
map <PII,int> id;
void check(PII t)
{
    if(id.find(t)==id.end()) id[t]=++bh;
    return;
}
void add(int x,int y,int z)
{
    // printf("%d %d %d\n",x,y,z);
    T[x].push_back(mp(y,z));
    T[y].push_back(mp(x,z));
}
vector <int> tree[maxn];
int st[maxn],p[maxn],top,cnt;
int fath[maxn];
void build(int now)
{
    int sz=tree[now].size();
    if(!sz) return;
    cnt=0;
    for(auto u:tree[now]) p[++cnt]=u;
    if(id.find(mp(now,1))==id.end()) p[++cnt]=1,sz++;
    sort(p+1,p+cnt+1,cmp);
    top=0; st[0]=0;
    for(int i=1;i<=sz;i++)
    {
        if(!top)
        {
            st[++top]=p[i];
            fath[p[i]]=0;
            continue;
        }
        int u=p[i],x=lca(u,st[top]);
        while(dep[x]<dep[st[top]])
        {
            if(dep[x]>=dep[st[top-1]]) fath[st[top]]=x;
            top--;
        }
        if(x!=st[top])
        {
            p[++cnt]=x;
            fath[x]=st[top];
            st[++top]=x;
        }
        fath[u]=x; st[++top]=u;
    }
    for(int i=1;i<=cnt;i++)
        check(mp(now,p[i]));
    for(int i=1;i<=cnt;i++) 
        if(fath[p[i]])
            add(id[mp(now,p[i])],id[mp(now,fath[p[i]])],dep[p[i]]-dep[fath[p[i]]]);
}
ll dis[maxn<<4];
int vis[maxn<<4];
ll dij(int S,int ed)
{
    for(int i=1;i<=bh;i++) dis[i]=inf,vis[i]=0;
    dis[S]=0;
    priority_queue <PLI> q;
    q.push(mp(0,S));
    while(!q.empty())
    {
        int u=q.top().second;
        q.pop();
        if(vis[u]) continue;
        vis[u]=1;
        for(auto to:T[u])
        {
            int v=to.first;
            if(dis[v]>dis[u]+to.second)
            {
                dis[v]=dis[u]+to.second;
                q.push(mp(-dis[v],v));
            }
        }
    }
    return dis[ed];
}
int main()
{
    freopen("travel.in","r",stdin);
    freopen("travel.out","w",stdout);
    scanf("%d%d%d",&n,&m,&q);
    int x,y;
    for(int i=1;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        G[x].push_back(y);
        G[y].push_back(x);
    }
    dfs(1,0);
    for(int i=1;i<=m;i++)
    {
        int p1,p2,u1,u2;
        scanf("%d%d%d%d",&p1,&u1,&p2,&u2);
        if(id.find(mp(u1,p1))==id.end()) tree[u1].push_back(p1);
        if(id.find(mp(u2,p2))==id.end()) tree[u2].push_back(p2);
        check(mp(u1,p1)); check(mp(u2,p2));
        add(id[mp(u1,p1)],id[mp(u2,p2)],1);
    }
    for(int i=1;i<=q;i++)
    {
        int p1,p2,u1,u2;
        scanf("%d%d%d%d",&p1,&u1,&p2,&u2);
        if(id.find(mp(u1,p1))==id.end()) tree[u1].push_back(p1);
        if(id.find(mp(u2,p2))==id.end()) tree[u2].push_back(p2);
        check(mp(u1,p1)); check(mp(u2,p2));
        qs[i]=id[mp(u1,p1)]; qt[i]=id[mp(u2,p2)];     
    }
    for(int i=1;i<=2e5;i++) 
        build(i);
    // for(int i=1;i<=3;i++)
    //     for(int j=1;j<=3;j++)
    //         printf("id of(%d %d):%d\n",i,j,id[mp(i,j)]);
    for(int i=1;i<=q;i++)
    {
        ll res=dij(qs[i],qt[i]);
        // printf("%d %d\n",qs[i],qt[i]);
        if(res!=inf)
            printf("%lld\n",res);
        else printf("impossible\n");
    }
    return 0;
}