python lru_cache 备忘（memoization）功能

装饰器 functools.lru_cache

functools.lru_cache 是非常实用的装饰器，它实现了备忘（memoization）功能。这是一项优化技术，它把耗时的函数的结果保存起来，避免传入相同的参数时重复计算。LRU三个字母是“Least Recently Used”的缩写，表明缓存不会无限制增长，一段时间不用的缓存条目会被扔掉。

生成第 n 个斐波纳契数这种慢速递归函数 ：

@clock

def fibonacci(n):

    if n < 2:

        return n

    return fibonacci(n-1) + fibonacci(n-2)

print(fibonacci(6))

上面打印出来可以看到浪费时间的地方很明显： fibonacci(1) 调用了 8 次， fibonacci(2) 调用了 5 次。

使用lru_cache缓存优化递归：

@functools.lru_cache(maxsize=128)

@clock

def fibonacci(n):

    if n < 2:

        return n

    return fibonacci(n-1) + fibonacci(n-2)

注意，必须像常规函数那样调用 lru_cache，这一行中有一对括号 @functools.lru_cache()，这是因为lru_cache 可以接受参数。

这样使用后fibonacci(1)和fibonacci(2)会直接从LRU缓存读取，不在进行函数调用计算了。

除了优化递归算法之外， lru_cache 在从 Web 中获取信息的应用中也能发挥巨大作用：

lru_cache 可以使用两个可选的参数来配置，它的签名是：

functools.lru_cache(maxsize=128, typed=False)

1. maxsize 参数指定存储多少个调用的结果。缓存满了之后，旧的结果会被扔掉，腾出空间。为了得到最佳性能， maxsize 应该设为 2 的幂。

2. typed 参数如果设为 True，把不同参数类型得到的结果分开保存，即把通常认为相等的浮点数和整数参数（如 1 和 1.0）区分开。

小示例：

@functools.lru_cache(maxsize=128, typed=True)

def deter_func(x, y):

    print('call func, calc ', x, y)

    return x + y

# call func, calc  1 2

print(deter_func(1, 2))

# call func, calc  4 2

print(deter_func(4, 2))

# not call, read from lru_cache

print(deter_func(1, 2))

因为 lru_cache 使用字典存储结果，而且键根据调用时传入的定位参数和关键字参数创建，所以被lru_cache 装饰的函数，它的所有参数都必须是可散列的。

cache_clear和cache_info

使用cache_info方法检索缓存统计信息：

# CacheInfo(hits=1, misses=2, maxsize=128, currsize=2)

print(deter_func.cache_info())

使用cache_clear方法重置结果缓存。

print(deter_func.cache_clear())

# CacheInfo(hits=0, misses=0, maxsize=128, currsize=0)

print(deter_func.cache_info())

缓存注意事项——什么是可以被记忆的

理想情况下，要记忆确定性的函数：

def deter_func(x, y)

    return x + y

deter_func是一个确定性函数，因为它总是会为相同的一对参数返回相同的结果。例如，如果您将2和3传入该函数，它将始终返回5。

非确定性函数：

def non_deter_func(x, y):

    if datetime.datetime.now().weekday() == 0:

        return x + y + x

    return x + y

这个函数是不确定的，因为它对于一个给定的输入的输出会根据星期几而变化：如果你在星期一运行这个函数，缓存将在一周中的任何一天返回陈旧的数据。

LRU Cache原理

LRU（Least recently used，最近最少使用）算法根据数据的历史访问记录来进行淘汰数据，其核心思想是“如果数据最近被访问过，那么将来被访问的几率也更高”。

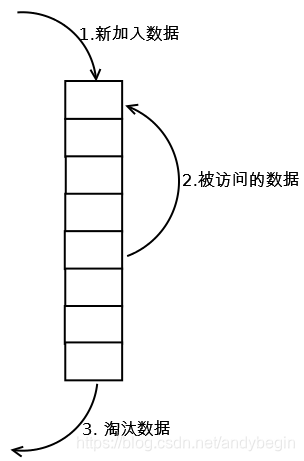
1.LRU Cache简单版，最常见的实现是使用一个链表保存缓存数据，如下图所示：

1. 新数据插入到链表头部；

2. 每当缓存命中（即缓存数据被访问），则将数据移到链表头部；

3. 当链表满的时候，将链表尾部的数据丢弃。

【命中率】当存在热点数据时，LRU的效率很好，但偶发性的、周期性的批量操作会导致LRU命中率急剧下降，缓存污染情况比较严重。

【复杂度】实现简单。

【代价】命中时需要遍历链表，找到命中的数据块索引，然后需要将数据移到头部。

2.LRU Cache复杂版—LRU-K

LRU-K中的K代表最近使用的次数，因此LRU可以认为是LRU-1。LRU-K的主要目的是为了解决LRU算法“缓存污染”的问题，其核心思想是将“最近使用过1次”的判断标准扩展为“最近使用过K次”。

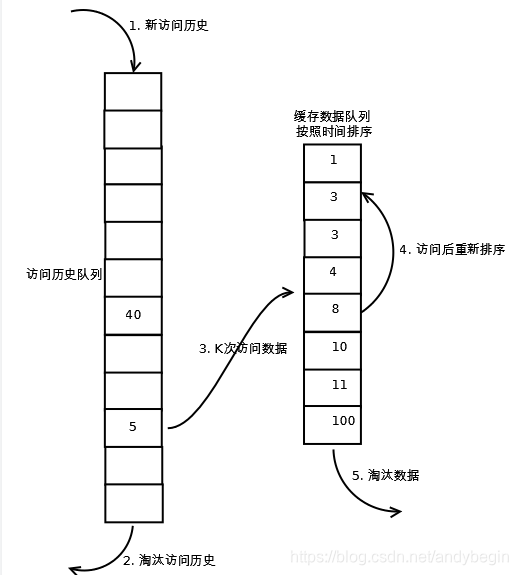
相比LRU，LRU-K需要多维护一个队列，用于记录所有缓存数据被访问的历史。只有当数据的访问次数达到K次的时候，才将数据放入缓存。当需要淘汰数据时，LRU-K会淘汰第K次访问时间距当前时间最大的数据。如下图所示：

1. 数据第一次被访问，加入到访问历史列表；

2. 如果数据在访问历史列表里后没有达到K次访问，则按照一定规则（FIFO，LRU）淘汰；

3. 当访问历史队列中的数据访问次数达到K次后，将数据索引从历史队列删除，将数据移到缓存队列中，并缓存此数据，缓存队列重新按照时间排序；

4. 缓存数据队列中被再次访问后，重新排序；

5. 需要淘汰数据时，淘汰缓存队列中排在末尾的数据，即：淘汰“倒数第K次访问离现在最久”的数据。