深度理解期望、方差偏差与方差偏差分解

最新推荐文章于 2025-02-10 19:30:11 发布
最新推荐文章于 2025-02-10 19:30:11 发布
阅读量3.9k 收藏 9
点赞数 1
分类专栏： 机器学习与人工智能 文章标签： 机器学习 人工智能 期望 方差
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/amao1998/article/details/110820146
版权
本文深入探讨了数学期望，包括离散分布和连续分布的期望，以及正太分布的概念。接着介绍了方差作为衡量数据离散程度的指标，并在机器学习的上下文中，解释了偏差-方差分解，如何评估模型的泛化能力。通过理解这些基本概念，有助于更好地理解和优化机器学习模型。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

前言

我们经常用偏差-方差分解形式来度量机器学习模型泛化能力的内容。本文将从数学基础来解释其演进过程。我们先从数学期望开始。

1、数学期望

概率论是描述现实世界的一个重要学科。我们从现实世界了解数学规律往往是通过一次一次的抽样开始的。我们没做一个事情就会是一次抽样。同样我们也通过做一个事情的经理（也就是多次抽样）来预测，本次做这件事情的成功概率。这本身就是机器学习或者人工智能的过程。所以期望一词也符合我们在场景中的一个定义。

当前期望在数学领域并不这样笼统，首先我们需要明确的是：期望的本质就是【均值】。同时期望又分为离散分布的期望与连续分布的期望。

1.1 离散分布的期望

首先看一下离散分布期望的原始定义

在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。

如果随机变量只取得有限个值或无穷能按一定次序一一列出，其值域为一个或若干个有限或无限区间，这样的随机变量称为离散型随机变量。

以上的表述非常的形而上，也不容易理解。那么我么可以用一些现实中的例子来转述一下，不过要时刻记得之前得到的一个结论：期望的本质就是【均值】

甲乙两人共进行10次打把练习，命中环数与次数的对应关系如下

甲 7环 8环 9环 10环
2次 4次 2次 1次
乙 7环 8环 9环 10环
1次 5次 4次 0次

如果我们想用一个指标来衡量这两个人的射击水平就可以用数学期望，可以做如下符号定义

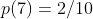p(x)代表射击出现的概率，假如我们定义甲打出7环的概率为p(7)=2 / 10 则其他概率可以进行同样的定义，则我们可以根据期望的定义计算甲的射击水平

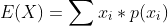
E(X)=\sum x_i*p(x_{i}) 

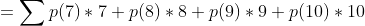
           =\sum p(7)*7+p(8)*8+p(9)*9+p(10)*10

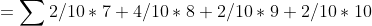
           =\sum 2/10*7+4/10*8+2/10*9+2/10*10

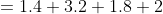
           =1.4+3.2+1.8+2

           

最低0.47元/天 解锁文章
深度学习：偏差（bias）和方差（Variance）
南淮北安的博客
10-21 1万+
文章目录一、期望、概率论方差、均方差二、为什么会有偏差和方差三、偏差、方差、噪声是什么？1. 简述偏差、方差、噪声2. 数学公式定义偏差、方差、噪声四、泛化误差、偏差和方差的关系？五、用图形解释偏差和方差六、偏差、方差囧境七、偏差、方差与过拟合、欠拟合的关系？八、偏差、方差与模型复杂度的关系九、偏差、方差与bagging、boosting的关系？十、偏差、方差和K折交叉验证的关系？十一、如何解决偏...
方差与偏差的意义与推导过程
Mr_tianyanxiaobai的博客
12-12 2248
基本概念 偏差(bias)：预测结果与真实值之间的差异，排除噪声的影响，偏差是某个模型输出的样本误差。偏差是模型无法准确表达数据关系所导致的，比如模型过于简单，非线性的数据关系采用线性模型建模，偏差较大的模型是错的模型； 方差(variance): 模型方差不是针对某一个模型输出样本进行判定，而是指多次模型输出的结果之间的离散差异，注意这里写的多次模型，即同一模型不同时间的输出结果方差较大。方差是由训练集的数据不够导致，一方面量 (数据量) 不够，有限的数据集过度训练导致模型复杂。即过拟合。 总结： B
机器学习中Bias（偏差）和Variance（方差）
Microstrong
04-05 2576
先占个坑吧！慢慢补！
偏差-方差分解bias-variance decomposition
sunlanchang的博客
04-23 1417
方差、偏差的直观意义 维基百科定义： Var⁡(X)=E[(X−μ)2]其中μ=E(X) \operatorname{Var}(X)=\mathrm{E}\left[(X-\mu)^{2}\right] 其中\mu=\mathrm{E}(X) Var(X)=E[(X−μ)2]其中μ=E(X) 在给定数据集中 方差： var⁡(x)=ED[(f(x;D)−f‾(x))2] \operatorname...
机器学习 - 理解偏差-方差分解
分享技术人生的学习笔记和过往心得，与志同道合者共同进步
02-10 1104
为了避免过拟合，我们经常会在模型的拟合能力和复杂度之间进行权衡。拟合能力强的模型一般复杂度会比较高，容易导致过拟合。相反，如果限制模型的复杂度，降低其拟合能力，又可能会导致欠拟合。因此，如何在模型的拟合能力和复杂度之间取得一个较好的平衡，对一个机器学习算法来讲十分重要。偏差-方差分解(Bias-Variance Decomposition)为我们提供了一个很好的分析和指导 工具。
2020-11-29
liaoqing1999的博客
11-29 1068
20 20.某产品的次品率为0.1,检察员每天检查四次,每次随机的取10件产品进行检验,如果发现其中的次数多于1,就去调整设备,以X表示一天中调整设备的次数,求E(X). 解：知识点：（二项分布、分布律、E(X)） 设一次抽检中次品数为Y，则Y符合 Y~B（10，0.1）的二项分布 ∴P(调整设备)=P(Y>1)=1−P(Y=0)−P(Y=1)=1−0.910−C1010.990.1=0.2639 \therefore P(调整设备)=P(Y>1) = 1-P(Y=0)-P(Y=1)=1-0.9
谈谈偏差-方差分解
m0_73765519的博客
07-06 658
为了避免过拟合，我们经常会在模型的拟合能力和复杂度之间进行权衡．拟合能力强的模型一般复杂度会比较高，容易导致过拟合．相反，如果限制模型的复杂度，降低其拟合能力，又可能会导致欠拟合．因此，如何在模型的拟合能力和复杂度之间取得一个较好的平衡，对一个机器学习算法来讲十分重要．偏差-方差分解（Bias-Variance Decomposition）为我们提供了一个很好的分析和指导工具所以模型的选择不能单从训练集上的错误率入手，盲目的看重训练集可能会导致过拟合，那么我们应该如何选择模型？
偏差-方差分解 Bias-Variance Decomposition(转载)
weixin_30415801的博客
01-21 234
转载自http://www.cnblogs.com/jmp0xf/archive/2013/05/14/Bias-Variance_Decomposition.html 完全退化了，不会分解，看到别人的分解方法了，留存。 以下为转载： -----我是转载的昏割线----- 设希望估计的真实函数为 f=f(X) 但是观察值会带上噪声，通常认为其均值为0 ...
偏差方差分解
zhulf0804的博客
01-10 3895
偏差方差分解——Bias-Variance Decomposition: expected loss = bias2 + variance + noise   ：the prediction function trained on data set D ：the optimal function,for regression,   Expected loss of regression
机器学习的误差从何而来？“偏差-方差分解 ” |李宏毅机器学习【3】
python令狐冲
09-02 1038
 对于机器学习算法，可以通过实验估计其泛化性能，但是为什么不同算法在不同训练集上有不同的错误率？欠拟合和过拟合的深层原因到底是什么？“偏差-方差分解”(Bias-Variance decomposition)是解释算法泛化性能的一种常用工具。 顾名思义，偏差-方差分解就是试图把学习算法的期望泛化错误率分解为偏差和方差。偏差指的是期望预测和真实结果之间的偏离程度，而方差指的是因相同数量的训练集的...
机器学习偏差、方差、泛化误差的完整总结
大柳的博客
02-10 4546
机器学习算法的最终目标是最小化期望损失风险（即机器学习模型在任意未知测试样本上的表现），但由于数据的真实分布我们通常是不知道的，我们可用的信息来自于训练数据，因此，机器学习的学习目标往往会转化为最小化经验风险。优化算法对经验风险最小化问题进行求解，并在算法结束的第TTT次迭代中输出模型。我们希望所学习到的该模型对未知数据预测的误差尽可能小，这里的误差我们就将其定义为机器学习算法的泛化误差（generalization error）：Rexp⁡(f^)=EP[L(Y,f^(X))]=∫X×YL(y,f^(x)
偏差-方差分解
To_be_thinking的博客
03-21 823
对于测试样本x\bm{x}x，令yDy_{D}yD​为x\bm{x}x在数据集中的真实标记，f(x;D)f(\bm{x};D)f(x;D)为训练集DDD上 学得模型fff在x\bm{x}x上的预测输出。以回归问题为例，学习算法的期望预测为： f‾(x)=ED[f(x;D)]\overline{f}(x)=E_{D}[f(\bm{x};D)]f​(x)=ED​[f(x;D)] 使用样本数相同的不同的...
样本方差的期望_如何理解方差和偏差
weixin_39980298的博客
12-09 1141
这是我在学习李宏毅老师机器学习课程时记录的笔记，并不是一个全面的记录而只记录我认为比较关键的知识点，起到知识梳理和温故知新的作用。对较为简单的点只放上PPT和一点记录，对自认为重点的内容会多记录一些理解。本文首发于个人公众号“程序员与机器学习”，记录自己的学习笔记和心得，欢迎来交流，欢迎批评指导。1上图中，我们把回归比喻成打靶，为真实的数值，位于靶中心，为模型的预测值。可见，预测值的误差来自于偏差...
【机器学习】偏差-方差分解Bias-variance Decomposition
qq_32742009的博客
08-28 2万+
偏差-方差分解(Bias-Variance Decomposition) 偏差-方差分解(Bias-Variance Decomposition)是统计学派看待模型复杂度的观点。Bias-variance分解是机器学习中一种重要的分析技术。给定学习目标和训练集规模，它可以把一种学习算法的期望误差分解为三个非负项的和，即样本真实噪音noise、bias和 variance。 noise 样本真实...
机器学习系列5---偏差和方差分解
qq_35667901的博客
05-28 2255
机器学习的目的就是通过选择合适的算法确定输入和输出变量之间的映射关系，不同学习算法的对比指标一般是对应模型的泛化性能，但是在实际分析过程中模型泛化性能不是单一成分，不同数据集划分或者样本选择均会对泛化性能的不同部分产生影响，一般将学习算法对应模型的泛化误差分为两部分：偏差（预测集）+方差（训练集），具体推导过程如下： 假设对于测试样本，令对应变量标记为，真实输出为；训练集 D 的模型输出为，则对于测试样本，基于训练集模型的期望输出为： ...
期望、方差、偏差、标准差、均方差、协方差、相关系数、协方差矩阵
xingsongyu的博客
11-22 463
原文： https://blog.youkuaiyun.com/fisherming/article/details/79774830 https://blog.youkuaiyun.com/siyue0211/article/details/80309799
[机器学习必知必会]泛化误差率的偏差-方差分解
热门推荐
TOMACAT的博客
08-12 3万+
一、期望泛化误差的偏差-方差分解 偏差-方差分解试图对机器学习算法的期望泛化误差率进行拆解。 记为测试样本，为训练集D上学习得到的模型在上的预测输出，为在数据集中的标记，为的真实标记。 对算法的期望泛化误差进行分解： 得到： 即泛化误差可分解为偏差、方差与噪声之和。其中偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力；方差度量了同样大小的训练集的变...
偏差和方差的区别
最新发布
03-18
嗯，我现在要理解偏差和方差的区别。先回忆一下，这两个术语听起来都是统计学里的概念，可能和模型预测有关吧。偏差，可能是指预测值和真实值之间的差距？而方差，可能是指模型预测的波动情况？不过具体怎么区分呢？...
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值