ridge regression and lasso analysis-reproduced from csdn

岭回归、Lasso及其分析

2017年08月30日 15:06:27

阅读数：5381

基本概念

前段我们讨论了线性回归模型的原理策略，假定可以表示为 

f(xi)=∑k=1nwkxik+w0=wxif(xi)=∑k=1nwkxik+w0=wxi

其损失函数为： 

J(w)=12m∑i=1m(yi−f(xi))2=12m||y−Xw||2J(w)=12m∑i=1m(yi−f(xi))2=12m||y−Xw||2

 

最小二乘法求解可以得到最优解： 

w=(XTX)−1XTyw=(XTX)−1XTy

 

在讨论ridge regression 和 lasso 之前，先学习两个概念。

监督学习有两大基本策略，经验风险最小化和结构风险最小化。 
经验风险最小化策略为求解最优化问题，线性回归中的求解损失函数最小化问题即是经验风险最小化策略。 
经验风险最小化的定义为：

 

Remp(f)=1N∑i=1NL(yi,f(xi))Remp(f)=1N∑i=1NL(yi,f(xi))

 

其求解最优化问题，即： 

minf∈FRemp(f)=minf∈F1N∑i=1NL(yi,f(xi))minf∈FRemp(f)=minf∈F1N∑i=1NL(yi,f(xi))

由统计学知识知，当训练集数据足够大时，经验风险最小化能够保证得到很好的学习效果。当训练集较小时，则会产生过拟合现象。虽然对训练数据的拟合程度高，但对未知数据的预测精确度低，这样的模型不是适用的模型。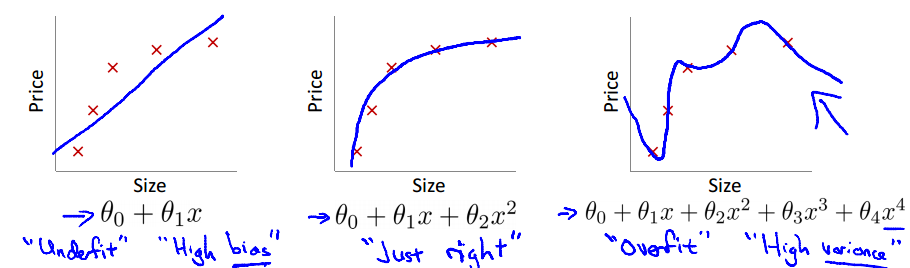 

 

结构风险最小化是为了防止过拟合现象而提出的策略。结构风险最小化等价于正则化，在经验风险上加上表示模型复杂度的正则化项或者称作罚项。在确定损失函数和训练集数据的情况下其定义为：

 

Rsrm(f)=1N∑i=1NL(yi,f(xi))+λJ(f)Rsrm(f)=1N∑i=1NL(yi,f(xi))+λJ(f)

 

其求解最优化问题，即： 

minf∈FRsrm(f)=minf∈F1N∑i=1NL(yi,f(xi))+λJ(f)minf∈FRsrm(f)=minf∈F1N∑i=1NL(yi,f(xi))+λJ(f)

通过调节λλ值权衡经验风险和模型复杂度

 

所要讨论的岭回归和Lasso，使用的是结构风险最小化的思想，在线性回归的基础上，加上对模型复杂度的约束。

岭回归与Lasso

岭回归其损失函数为： 

JR(w)=12∥y−Xw∥2+12λ∥w∥2JR(w)=12‖y−Xw‖2+12λ‖w‖2

 

wRˆ=(XTX+λI)−1XTywR^=(XTX+λI)−1XTy

 

Lasso其损失函数为： 

JL(w)=12∥y−Xw∥2+λ∑|wi|JL(w)=12‖y−Xw‖2+λ∑|wi|

 

由于Lasso损失函数的导数在0点不可导，不能直接求导利用梯度下降求解。引入subgradient的概念。

考虑简单函数，即x只有一维的情况下： 

h(x)=(x−a)2+b|x|h(x)=(x−a)2+b|x|

 

首先先定义|x||x|在0点的梯度，称之为subgradient。

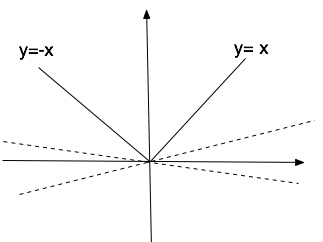
像上面图里画的，直观理解，函数在某一点的导数可以看成函数在这一点上的切线，那么在原点，因为这一点不是光滑的（左右导数不一样），所以可以找到实线下方的无数条切线，形成一个曲线族。我们就把这些切现斜率的范围定义为这一点的subgradient。也就是|x||x|在0点的导数是在-1到1范围内的任意值。

那么可以得到h(x)h(x)的导数：

 

f′(x)=⎧⎩⎨2(x−a)+cx,2a+d,2(x−a)−cx,if x>0 if x=0and−c<d<c if x<0 f′(x)={2(x−a)+cx,if x>0 2a+d,if x=0and−c<d<c 2(x−a)−cx,if x<0 

 

可以看出，当 −c<2a<c，x=0−c<2a<c，x=0时， f′(x)f′(x)恒等于0，也就是f(x)f(x)到达极值点。同时也可以解释Lasso下得到的解会稀疏的原因：因为当cc在一定范围内时，只要xx为0，f′(x)f′(x)就为0。

当xx拓展到多维向量时，导数方向的变化范围更大，问题就变得更复杂。常见的解决方法如下： 
1.贪心算法。每次先找到跟目标最相关的feature，然后固定其他系数，优化这一个feature的系数，具体求导也要使用到subgradient。代表算法有LARS，feature-sign search等。 
2.逐一优化。就每次固定其他的dimension，选择一个dimension进行优化，因为只有一个方向有变化，所以可以转化为简单的subgradient问题，反复迭代所有的dimension，达到收敛。代表算法有coordinate descent，block coordinate descent等，通过该方法求解得到的最优解w¯w¯为：

w¯j=sgn(wj)(∣∣wj∣∣−λ)+w¯j=sgn(wj)(|wj|−λ)+

其中wjwj表示其任一维度，(x)+(x)+表示取xx的正数部分，(x)+=max(x,0)(x)+=max(x,0)。

 

考虑Lasso和ridge的几何意义，如下图;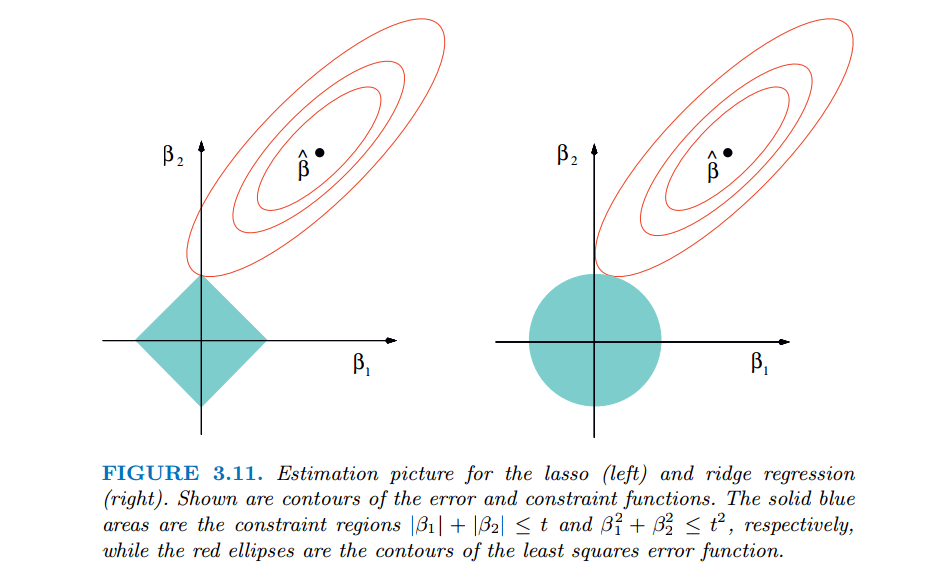 

红色的椭圆和蓝色的区域的切点就是目标函数的最优解，我们可以看到，如果是圆，则很容易切到圆周的任意一点，但是很难切到坐标轴上，则在该维度上取值不为0，因此没有稀疏；但是如果是菱形或者多边形，则很容易切到坐标轴上，使得部分维度特征权重为0，因此很容易产生稀疏的结果。

回归分析技术

线性回归是最常用的回归分析，其形式简单，在数据量较大的情况下，使用该方法可以得到较好的学习效果。 
线性回归在数据量较少的情况下会出现过拟合的现象，ridge、Lasso可以在一定程度上解决这个问题。 
由于Lasso得到的是稀疏解，由此可以看出，除了可以做回归分析外，还可以用于特征选取。

当然还有其他的回归分析： 
多项式回归，其自变量指数大于1。该方法可以诱导拟合一个高次多项式并得到较低的错误，但这可能会导致过拟合。需要经常画出关系图来查看拟合情况，并且专注于保证拟合合理，既没有过拟合又没有欠拟合。下面是一个图例，可以帮助理解具体如下图： 

逐步回归，自变量的选择是在一个自动的过程中完成的，其中包括非人为操作。标准逐步回归法做两件事情。即增加和删除每个步骤所需的预测。向前选择法从模型中最显著的预测开始，然后为每一步添加变量。向后剔除法与模型的所有预测同时开始，然后在每一步消除最小显着性的变量。这种建模技术的目的是使用最少的预测变量数来最大化预测能力。这也是处理高维数据集的方法之一。

ElasticNet回归，即岭回归和Lasso技术的混合，当存在多个相关特征时，Lasso 会随机挑选他们其中的一个，而ElasticNet则会选择两个。即在高度相关变量的情况下，它会产生群体效应。

逻辑回归，广泛用于分类问题。逻辑回归不要求自变量和因变量是线性关系，可以处理各种类型的关系。

还有其他模型，如Bayesian、Ecological和Robust回归等。

引用： 
http://blog.youkuaiyun.com/xbinworld/article/details/44276389