数据结构-堆

一、前言

堆就是用数组实现的二叉树，所以它没有使用父指针或者子指针。堆根据“堆属性”来排序，“堆属性”决定了树中节点的位置。

1.1 堆的种类

最大堆、最小堆分别是父节点大于/小于子节点的堆。这个性质就是“堆属性”，且对于任何节点都成立。

1.2 优先队列与堆的关系

优先队列： 优先队列是一种数据结构，它的作用是找出、返回、删除优先队列中的优先级最小的元素。
堆： 堆，也是一种数据结构；其中的二叉堆经常用于实现优先队列；本文就是介绍二叉堆实现的优先队列。

1.3 堆(二叉堆)与二叉搜索树的区别

’1.节点的顺序’
      二叉搜索树中，节点的顺序必须满足 left< root & root < right;堆中：只需要满足left<root & right<root；
’2.内存占用’
      普通树占用的内存空间比它们存储的数据要多。你必须为节点对象以及左/右子节点指针分配内存。堆仅仅使用一个数据来存储数组，且不使用指针。
’3.搜索效率’
在二叉树中搜索会很快，但是在堆中搜索会很慢。在堆中’搜索不是第一优先级’，因为使用堆的目的是将最大（或者最小）的节点放在最前面，从而快速的进行相关插入、删除操作。

1.4 父子节点的关系

parent(i) = i/2
left(i)   = 2*i 
right(i)  = 2*i + 1

2. 大顶堆

2.1介绍

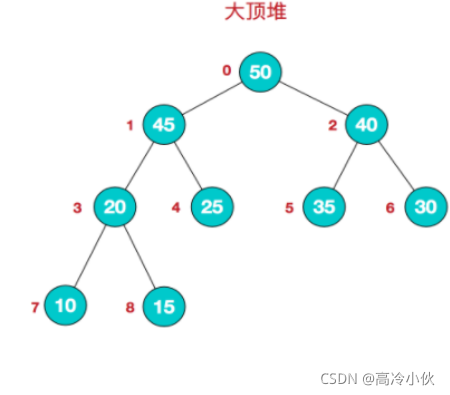
所谓大顶堆，就是指每个结点的值都大于或等于其左右孩子结点；因此，大顶堆的根节点为所有节点的最大值。

2.2堆的构造过程

const int maxn=100;
int n;
int Heap[maxn]; 
void Adjust(int low,int high){
	int k=low*2,r=low;
	while(k<high){
		if(k+1<high&&Heap[k+1]>Heap[k])
			k=k+1;
		if(Heap[k]>Heap[r]){
			//不符合堆条件，交换
			swap(Heap[k],Heap[r]);
			r=k;
			k=r*2; 
		}
		else break;
	}
}
void HeapSort(int Heap[]){
	for(int i=n/2-1;i>=0;i--){
		Adjust(i,n);
	}
}

动态图展示

2.3堆操作

下列代码介绍了大顶堆的增、删、查操作的实现：

int heap[2000010];
int heap_size;
void swap(int x,int y){
	int temp=heap[x];
	heap[x]=heap[y];
	heap[y]=temp;
}
void put(int x){//插入元素 
	heap[++heap_size]=x;
	int now=heap_size;
	while(now>1){
		int fa=now>>1;
		if(heap[fa]<=heap[now])break;
		swap(fa,now);
		now=fa;
	}
} 
int get(){//返回根节点(堆中的最大/最小值) 
	return heap[1];
}
int del(){//删除根节点 
   int now,next,res;
   res=heap[1];
   heap[1]=heap[heap_size--];
   now=1;
   while(now*2<=heap_size){
    	next=now*2;
    	if(next<heap_size&&heap[next+1]<heap[next]) next++;
    	if(heap[now]<=heap[next]) return res;
  		swap(now,next);
 	    now=next;                      
    } 
}