本文讨论了五个关于算法和数据结构的问题：使用BFS解决扩散问题，通过质因数分解计算约数总数，理解本质上升序列的动态规划解法，玩具蛇的深度搜索策略，以及优化后的游园安排LIS问题。博客提供了解题思路和关键代码片段，涵盖了搜索算法、数论、动态规划和序列分析等领域。
B.扩散
解题思路
就是简单BFS，只是需要考虑负数的情况；因为最多到[-2020,2020]，因此，全部起点进行[x+2500,y+2500]操作；
代码展示
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5;
/*
20312088
*/
struct node{
int x,y;
int step;
};
bool vis[10000][10000];
int dx[]={0,0,1,-1};
int dy[]={1,-1,0,0};
int main(){
queue<node>q;
node New;
New.step=1;
New.x=0+2500,New.y=0+2500;
q.push(New);
New.x=2020+2500,New.y=11+2500;
q.push(New);
New.x=11+2500,New.y=14+2500;
q.push(New);
New.x=2000+2500,New.y=2000+2500;
q.push(New);
int ans=0;
while(!q.empty()){
node temp=q.front();
q.pop();
vis[temp.x][temp.y]=1;
ans++;
for(int i=0;i<4;i++){
int fx=temp.x+dx[i];
int fy=temp.y+dy[i];
if(!vis[fx][fy]&&temp.step<=2020){//涉及次数问题一定要理清楚+用可以手算的样例试试
vis[fx][fy]=1;//!!这个一定要加
New.step=temp.step+1;
New.x=fx,New.y=fy;
q.push(New);
}
}
}
cout<<ans<<endl;
return 0;
}
总结
但是在考试的没做出来，而且又尝试一遍，还是有问题~~；分析了下原因，一个是因为自己广搜不熟练，不知道vis[x][y]放在哪里；另一个就是对于步数的边界条件判断错误。
C.阶乘约数
解题思路
我们只需要知道一个公式就可以：
一个数n=p[1]^e1*p[2]^e2~~~
·这里的p[i]是它的质因子，ei是因子个数
则有sum(n)=(e1+1)*(e2+1)~~*(ei+1);
sum(n)表示n的约数总个数；
代码展示
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5;
/*
数论
39001250856960000
*/
int prim[105];
int main(){
for(int i=1;i<=100;i++){
int k=i;
for(int j=2;j*j<=i;j++){//必须是i，因为必须保证 j*j<=i,才能完全考虑
while(k%j==0){
prim[j]++;
k=k/j;
}
}
if(k!=1)prim[k]++;
}
long long ans=1;
for(int i=2;i<=100;i++){
if(prim[i]){//阿sir，都不会区分 ==0和!=0了？？
ans*=(prim[i]+1);
cout<<ans<<" "<<prim[i]+1<<endl;
}
}
cout<<ans<<endl;
return 0;
}
总结
就是数论知识，但是不知道的话也可以现场推导；
D.本质上升序列
解题思路
考试的时候想到的是深搜，但是估计了下时间，到考试结束都跑不出来~；
广搜
1.根据题目的样例，不难观察出，长度为2的子串是在长度为1的子串基础上扩展来的~~
2.所以可以利用广搜的层次性，初始化<string,int>即子串和它的末尾下标；
3.然后广搜即可；
4.需要注意的是，初始话的时候对于重复字母的判断：
代码展示
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#include<map>
using namespace std;
#define mk make_pair
const int inf=0x3f3f3f3f;
typedef long long ll;
int n,m,ans;
char s[500]="tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl";
/*
3616159
3616159
广搜的层次性？？
与深搜不同，深搜是一直得到一个子串，；
*/
map<string,bool>vis;
int main()
{
queue<pair<string,int> >q;//子串string的末端节点是pos
while(!q.empty())q.pop();
int l=strlen(s);
for(int i=0;i<l;i++){
if(!vis[s[i]+""]){
q.push(mk(s[i]+"",i));//mk是啥？？
vis[s[i]+""]=1;
}
}
int ans=0;
while(!q.empty()){
string str=q.front().first;
int kt=q.front().second;
q.pop();
ans++;
cout<<"A "<<str<<endl;
for(int i=kt+1;i<l;i++){
if(s[kt]<s[i]&&!vis[str+s[i]]){
q.push(mk(str+s[i],i));
vis[str+s[i]]=1;
}
}
}
cout<<ans<<endl;
return 0;
}
总结
LIS、LCS等几个经典动规问题都要了解；
E.玩具蛇
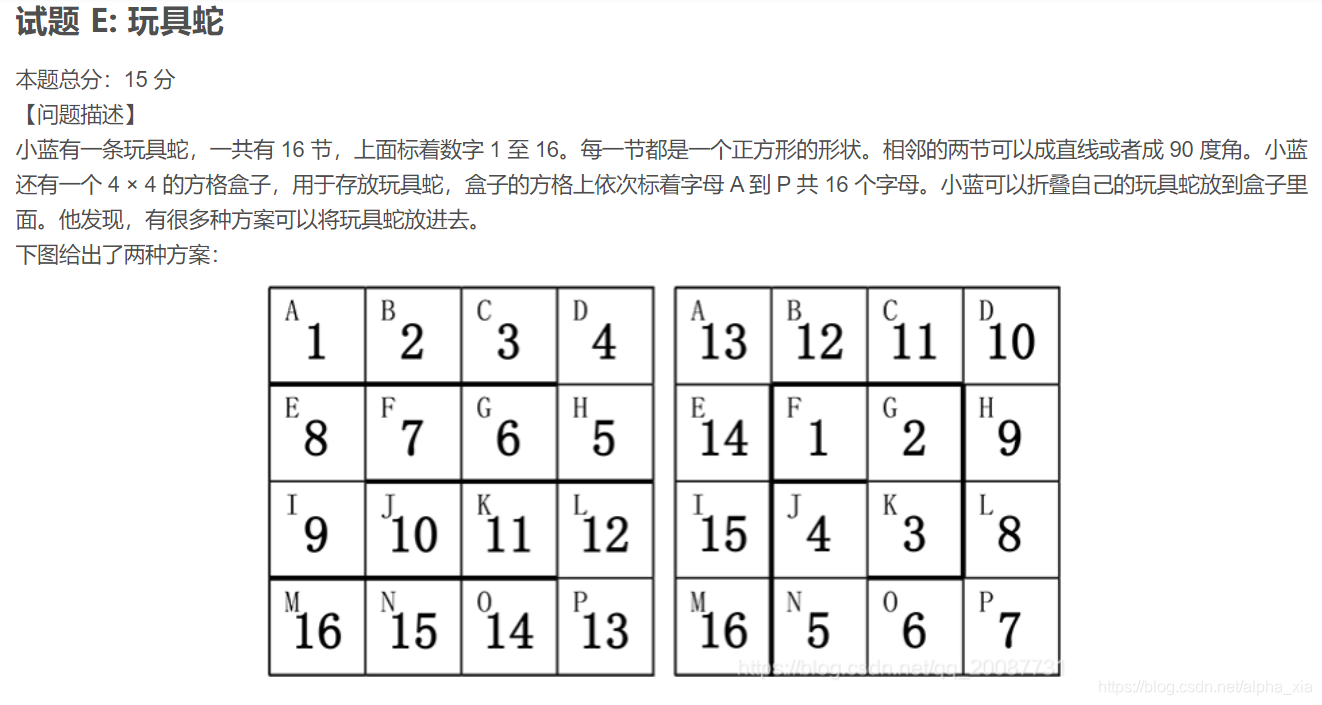
解题思路
简单的深搜，考试的时候脑子短路，没想起来~
代码展示
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5;
/*
*/
int ans;
int dx[]={0,0,1,-1};
int dy[]={1,-1,0,0};
bool vis[20][20];
void DFS(int x,int y,int k){//操，一定要用文字理一遍DFS的意思！~！！！
// cout<<x<<" "<<y<<" "<<k<<endl;
if(k>=16){
ans++;
return;
}
for(int i=0;i<4;i++){
int fx=x+dx[i];int fy=y+dy[i];
if(fx>=1&&fx<=4&&fy>=1&&fy<=4){
if(!vis[fx][fy]){
vis[fx][fy]=1;
DFS(fx,fy,k+1);//淦
vis[fx][fy]=0;
}
}
}
}
int main(){
for(int i=1;i<=4;i++){
for(int j=1;j<=4;j++){
memset(vis,0,sizeof(vis));
vis[i][j]=1;
DFS(i,j,1);
cout<<ans<<endl;
}
}
return 0;
}
总结
深搜时，一定要注意对递归边界的判断；我的方法就是定义深搜函数时搞清楚这个深搜的作用。
F.皮亚诺曲线
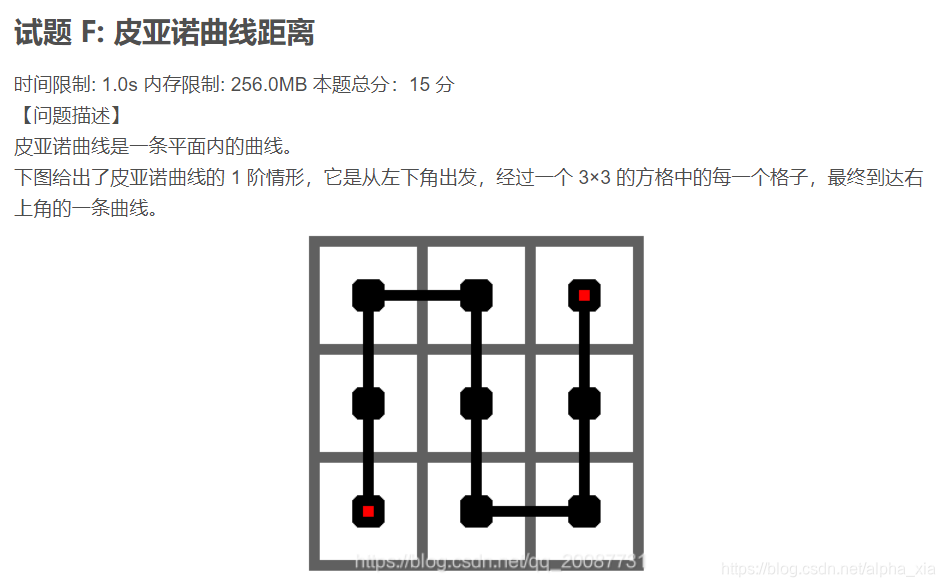
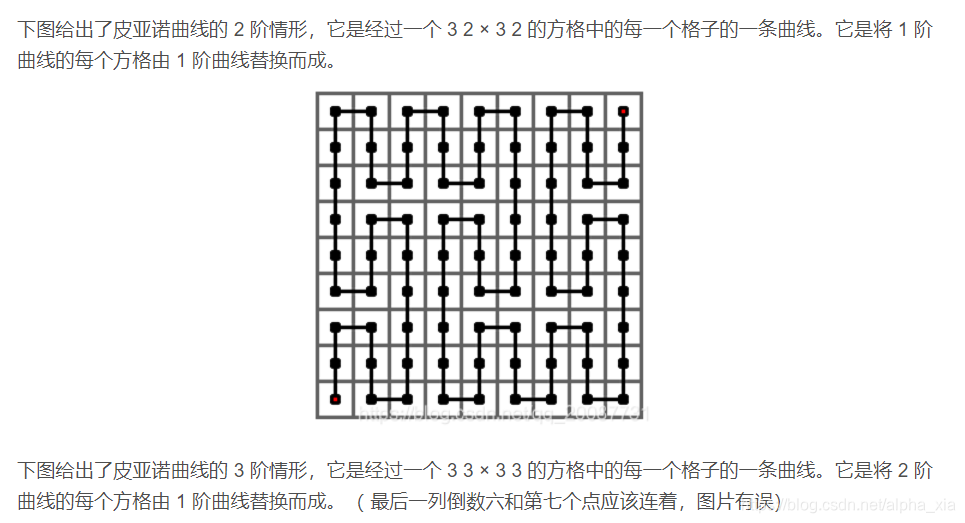
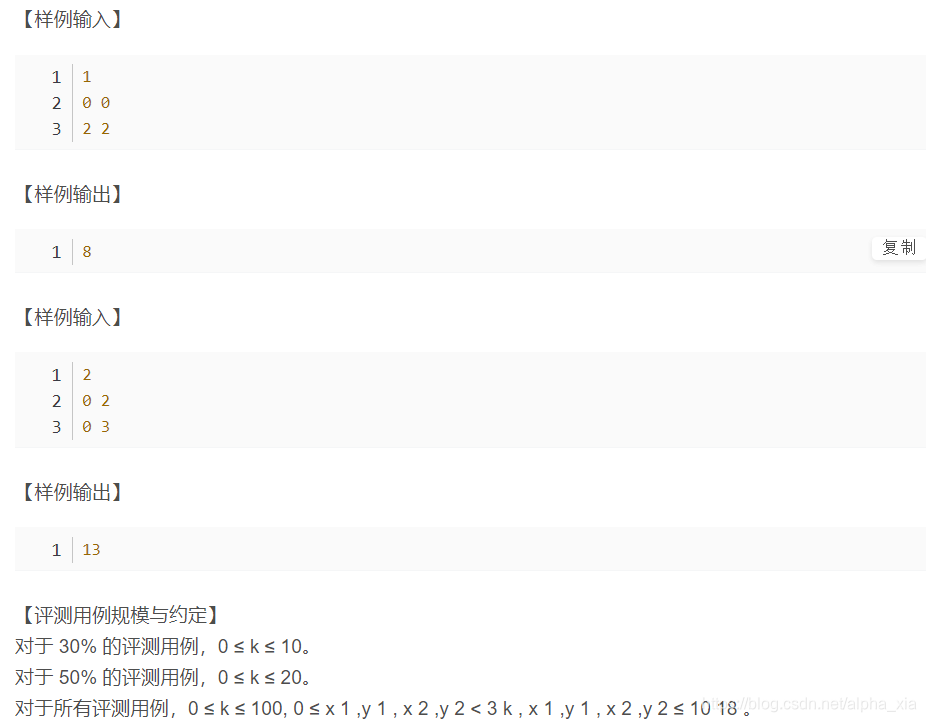
解题思路
代码展示
总结
G.游园安排
解题思路
很明显地求LIS，但是需要两个优化：
1.时间复杂度要为O(n*logn)；
2.求出递增序列
1.普通的动态规划求法是用dp[i]表示以s[i]结尾的递增序列长度，但是这种方法的时间复杂度为O(n^2);
2.可以用B[i]表示长度为i的递增序列结尾元素是s[i];然后遍历一遍序列：
B[i]<s[i] : B[++len]=s[i];
否则：找出B中第一个大于等于s[i]的元素下标f，标记为新的长度为f的递增序列；
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5;
/*
单调递增序列
WoAiLanQiaoAiBeiQiao
*/
vector<string>q;
string B[10010];
int pre[10010];
string ans[10010];
int serach_index(string B[],int len,string x){//求第一个>=x的值
int lef=1,rig=len;//??
while(lef<rig){
int mid=lef+rig >> 1;
if(B[mid]<=x){
rig=mid+1;
}
else lef=mid;
}
return lef;
}
int main(){
string s;
cin>>s;
int last=0;
for(int i=0;i<s.size()-1;i++){
if(s[i+1]>='A'&&s[i+1]<='Z'){
string name=s.substr(last,i-last+1);
last=i+1;
q.push_back(name);
}
}
q.push_back(s.substr(last,s.size()-1-last+1));
// cout<<"q.size "<<q.size()<<endl;
int l=q.size();
int maxi,maxlen=0;
int len=1;B[1]=q[0];
pre[0]=1;//初始化
for(int i=1;i<l;i++){
if(B[len]<q[i]){
B[++len]=q[i];
pre[i]=len;
}
else {
//int f=serach_index(B,len,q[i]);//这个lower_bound有点意思
int f=lower_bound(B+1,B+1+len,q[i])-B;
B[f]=q[i];
pre[i]=f;
//cout<<f<<endl;
}
}
// for(int i=0;i<l;i++)
// cout<<q[i]<<" "<<pre[i]<<endl;
int temp=len;
for(int i=l-1;i>=0;i--){
if(pre[i]==len){
ans[len]=q[i];
len--;
}
}
for(int i=1;i<=temp;i++)
cout<<ans[i];
return 0;
}
总结
H.答疑
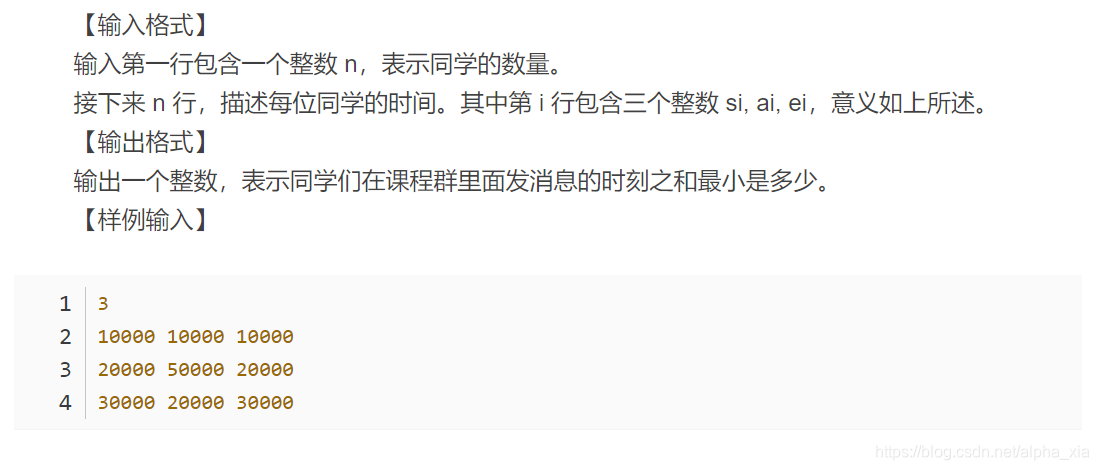
解题思路
设结果中的第i个请教的同学进入+答疑的时间是q[i]，进入+答疑+离开的时间是p[i];
那么总时间是：q[1]+(p[1]+q[2])+(p[1]+p[2]+q[3])=2p[1]+p[2]+(q1+q2+q3)；
所以就是按时间排序~~~；
代码展示
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5;
/*
5
2 435 76
34 57 78
676 8 87
587 78 8
346 767 66
*/
struct node{
int w,s;
};
node stu[1005];
bool cmp(node a,node b){
if(a.s!=b.s)
return a.s<b.s;
return a.w<b.w;
}
int main(){
int n;
cin>>n;
for(int i=0;i<n;i++){
int a,b,c;
cin>>a>>b>>c;
stu[i].w=a+b;
stu[i].s=stu[i].w+c;
}
sort(stu,stu+n,cmp);
ll ans=0,temp=0;
for(int i=0;i<n;i++){
ans=ans+temp+stu[i].w;//上一个学生+当前需要用时
temp=temp+stu[i].s;//更新
// cout<<ans<<endl;
}
cout<<ans<<endl;
return 0;
}
总结
我考试的时候也是瞎猜，考完之后看大佬的题解，好像还蒙对了~~~；
I.
解题思路
总结
J.质数行者
解题思路
1.暴搜混分
考试的时候用的记忆化暴搜混分~
估计了时间，也就能过一个样例~
而且这题也不能用广搜，因为这题没有“层次性”；
代码展示
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5;
/*
1.记忆化搜索的前提是基本搜索
2.搞一搞牛逼筛法
3.暴力求稳
A. Tit for Tat
*/
int vis[305][305][305];
vector<int>step;
bool Judge(int x){
for(int i=2;i*i<=x;i++)
if(x%i==0)return false;
return true;
}
int len;
void init(){
for(int i=2;i<=1000;i++){
if(Judge(i))step.push_back(i);
}
len=step.size();
}
int n,m,w;
int ans;
int a1,b1,c1,a2,b2,c2;
bool Judge2(int x,int y,int z){
if(a1==x&&b1==y&&c1==z)return 0;
if(a2==x&&b2==y&&c2==z)return 0;
return true;
}
int DFS(int x,int y,int z){//我他妈能把变量搞混~~~
if(Judge2(x,y,z)==false)return 0;
if(x==n&&y==m&&z==w){
return 1;
}
int sum=0;
for(int i=0;i<len;i++){
if(x+step[i]<=n)
sum+=DFS(x+step[i],y,z);
if(y+step[i]<=m)
sum+=DFS(x,y+step[i],z);
if(z+step[i]<=w)
sum+=DFS(x,y,z+step[i]);
}
vis[x][y][z]=sum;
return sum;
}
int main(){
init();
cin>>n>>m>>w;
cin>>a1>>b1>>c1;
cin>>a2>>b2>>c2;
cout<<DFS(1,1,1)<<endl;
return 0;
}
总结
参考博客
https://blog.youkuaiyun.com/qq_20087731/article/details/109691930
扫一扫
6622
到【灌水乐园】发言
