【拓扑排序+位运算】可达性统计

最新推荐文章于 2025-07-17 15:21:33 发布

原创最新推荐文章于 2025-07-17 15:21:33 发布 · 187 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #AC #拓扑排序 #位运算

刷题笔记专栏收录该内容

53 篇文章

订阅专栏

本博客介绍了如何利用C++解决有向无环图（DAG）的拓扑排序问题，并结合bitset进行节点信息的高效存储。首先，通过拓扑排序得到节点的正确顺序，然后从末端开始遍历，用bitset存储每个节点的可达状态，最终输出每个节点可达节点的数量。这种方法适用于处理大量节点的情况，通过位运算提高效率。

题目描述

https://www.acwing.com/problem/content/166/

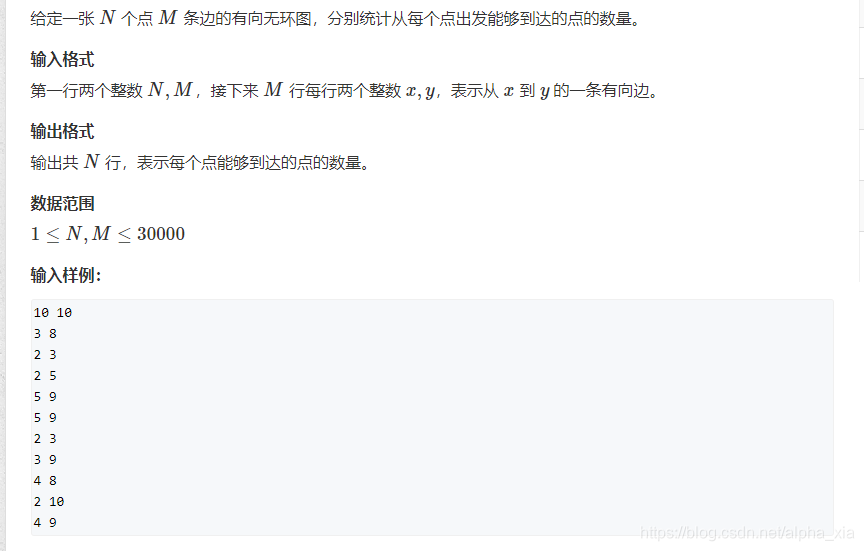
在这里插入图片描述

解题思路

1.题目中说明给定的图是一个`有向无环图`，由此我们可以想到是拓扑排序；
2.不难想到这题的思路是先遍历一个节点能到达的所有节点，再把所有节点的能到的节点去重相加,即：
	f[x]=sum(f[G[x][i]]),i=[0,G[x].size()];
3.但是需要考虑的问题是如何保存每个节点的信息。由于节点过多，只能使用二进制存储；即bitset<size>f[maxn]；
4.值得注意的是，我们在遍历相加的时候，应该从拓扑序的末端开始，因为从起点开始的化，f[x]会在后面遍历时更新，导致结果不准确；

代码展示

#include<bits/stdc++.h>
using namespace std;
const int maxn=3e4+10;
/*
思路:
	
*/
int lev[maxn];
vector<int>G[maxn];
vector<int>topsort;
bitset<maxn>f[maxn];
int main(){
	int n,m;
	cin>>n>>m; 
	while(m--){
		int a,b;
		cin>>a>>b;
		lev[b]++;
		G[a].push_back(b);
	}
	queue<int>q;
	for(int i=1;i<=n;i++)
		if(!lev[i])q.push(i);
	while(!q.empty()){
		int temp=q.front();
		q.pop();
		topsort.push_back(temp);
		for(int i=0;i<G[temp].size();i++){
			--lev[G[temp][i]];
			if(lev[G[temp][i]]==0)q.push(G[temp][i]);
		}
	}
	//拓扑排序，得到拓扑序
	int l=topsort.size()-1;
	for(int i=l;i>=0;i--){
		int temp=topsort[i];
		f[temp][temp]=1;
		for(int i=0;i<G[temp].size();i++){
			f[temp] |= f[G[temp][i]];
		}
	} 
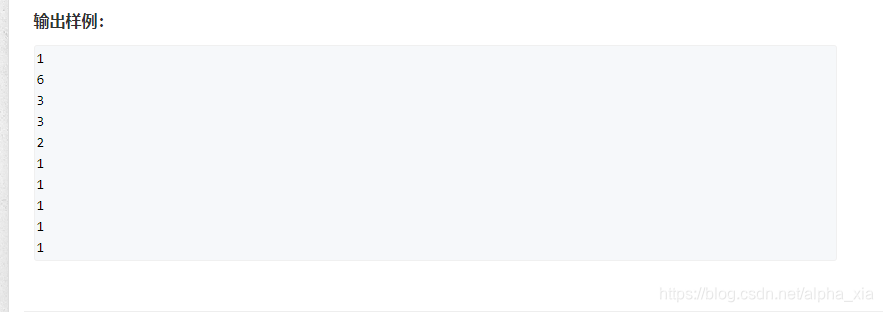
	for(int i=1;i<=n;i++)
		cout<<f[i].count()<<endl;
   return 0;
   
}

总结

bitset

1.bitset是c++STL库中封装好的类型，常用于状态压缩；
在这里插入图片描述

1.bitset<size>f
	size表示该位图的尺寸；
2.f.count()
	因为位图的初始值是0，所有该函数也可以表示位图中 1 的个数
3.f.set(pos,val)
	当set()中无参数时，表示设置位图中的所有位
	set中有参数时，表示设置单一位的值
4.f.reset()
	表示清空所有位；