能量收集CRSN中联合优化策略

能量收集认知无线电传感器网络中的联合频谱接入与传输功率管理

摘要

本文研究了能量收集认知传感器节点在时隙化方式下运行时，利用信道条件及能量收集状态的因果知识，进行频谱接入与传输功率的联合优化。考虑到感知不完美因素，我们将该联合优化问题建模为一个无限时域离散时间马尔可夫决策过程（MDP），其中认知传感器的目标是最大化长期期望吞吐量。我们提出了一种最优策略，用于确定频谱接入决策以及功率等级。结果表明，最优长期期望吞吐量随着电池可用能量的增加而不减小。此外，我们引入了一种低复杂度策略，并证明最优低复杂度策略关于电池可用能量具有阈值结构。同时提出了一种高效算法以求解最优低复杂度策略。最后，数值结果验证了所提出策略的优越性。

关键词 ：能量收集；认知无线电；马尔可夫决策过程；传感器网络。

1 引言

认知无线电（CR）（Li 等，2014；Zhang 等，2017； Maherin 和 Liang，2013；He 等，2016；Li 等， 2016）使次用户（SUs）能够利用主用户（PUs）留下的未使用频谱资源，为提高无线频谱效率以缓解频谱稀缺问题提供了有前景的途径。认知无线电传感器网络（CRSNs）（Hu 等，2012）作为一种重要的认知无线电网络，是将具备认知无线电能力的传感器作为次用户实现的无线传感器网络（WSNs）（Monemian 等， 2016）。在 CRSNs 中，可通过机会式接入授权频谱来解决由 IEEE 802.11 和蓝牙（IEEE 802.15.1）等新兴网络标准共存引起的非授权频谱饱和问题。此外，如 Akan 等（2009）和 Vijay 等（2011）所述，CRSNs 有助于减少拥塞和过度分组丢失，从而提高传输的可靠性（Jamal 等，2015）。

除了在无线传感器网络中引入认知无线电所带来的上述潜在优势外，还引发了许多新的研究问题。具体而言，在认知无线电传感器网络中，为了利用空闲频谱并保护主系统，认知传感器节点需要进行周期性频谱感知，并对频谱接入的可用性做出决策。这些特殊功能及其后续的数据传输导致传感器节点的能耗较高，而传统上这些节点是由电池供电的。尽管节能以及更换或充电电池可在一定程度上延长传感器节点的工作时间，但这些技术通常成本较高，并且在某些情况下操作不便甚至不可行（赵等人，2016）。一种面向能量受限的认知无线电传感器网络的新兴技术是能量收集（EH）（Bae 和 Baek，2016；Shi 等人，2017，2016）。来自可再生 能源的能量可以为传感器节点的电池充电，使认知无线电传感器网络有可能无需外部电源线或定期更换电池而持续运行（朴和洪，2013）。此外，利用收集的能量为传感器节点供电还可以减少能耗带来的碳排放，提升无线网络的环保性。因此，将能量收集技术融入认知无线电传感器网络，使得构建可持续且环境友好的传感器网络成为可能。

本文考虑一个时隙化的EH CRSN，该网络由一对认知传感器节点（记为次用户）组成。这些次用户配备有有限容量电池，并完全依靠从周围环境收集的能量供电。采用Zheng等人（2013，2010）提出的联合优化技术来提升EH CRSN系统的性能。具体而言，我们旨在对次用户的频谱接入决策和传输功率进行联合优化，以在满足能量因果性约束的条件下最大化长期期望吞吐量。能量因果性约束要求在任意时刻，能量消耗不得超过截至目前已收集能量的总量。在每个时隙开始时，次用户需要做出适当的频谱接入决策，以获得最优性能。如果次用户决定进入睡眠模式，则会保存收集的能量，但代价是失去了传输数据的机会。如果次用户决定进行频谱感知，则在频谱空闲的情况下有机会传输数据。然而，频谱感知会在时间和能量开销方面带来额外的系统成本。因此，需要精心设计频谱接入策略，以优化次用户的性能。以往的研究已在Park 和 Hong (2013)、Park 等人 (2013) 和 Park 等人 (2012) 中探讨了次用户的频谱接入策略。然而，仅调度频谱接入（朴和洪，2013；朴等人， 2013，2012）无法充分捕捉当次用户面临时变信道条件时的动态特性。事实上，次用户的发射功率自适应在其性能中也起着关键作用。例如，在深度衰落信道下，次用户必须降低其传输功率以节省能量。但过于保守的传输功率分配可能导致能量溢出，未能充分利用收集的能量。相反，当信道条件良好时，次用户需要提高其传输功率。然而，过于激进的发射功率分配可能导致电池在下次充电周期前能量过早耗尽。因此，次用户的信道波动和电池充电过程的复杂动态性，以及系统开销（由频谱感知引起的时间和能耗）带来的额外负担，要求对频谱接入和传输功率进行联合优化。

本工作的主要贡献总结如下：

• 在考虑感知不完美、信道状态变化以及电池能量补充过程的情况下，我们研究了频谱接入与传输功率分配的联合优化，以最大化次用户的长期期望吞吐量。上述设计问题被建模为一个折扣无限时域的马尔可夫决策过程（MDP）。
• 通过在MDP中应用值迭代方法，我们提出了最优策略，该策略根据信道衰落、收集的能量和电池存储的动态变化，确定频谱接入决策以及传输功率。此外，证明了最优策略所获得的长期期望吞吐量随电池可用能量的增加而非递减。
• 为了降低计算复杂度，我们提出了一种低复杂度策略，并证明最优低复杂度策略在电池可用能量方向上具有阈值结构，数值结果验证了该结构的有效性。利用这一阈值结构，提出了一种高效算法来获得最优低复杂度策略。

我们提供了广泛的数值结果，以评估所提出的策略的性能，并表明与几种替代策略相比，我们所提出的策略实现了显著增益。此外，还研究了各种系统参数对所提出策略性能的影响。

本文的其余部分组织如下。第2节介绍了能量收集和认知无线电技术的最新研究进展。在第3节中，我们提出了主网络模型和认知无线电网络模型。在第4节中，我们将频谱接入与传输功率分配的联合优化问题建模为一个马尔可夫决策过程。在第5节中，我们介绍了最优策略和最优低复杂度策略。第6节给出了数值结果。第7节对全文进行总结。

在本文中， Z+表示非负整数集合。我们记[x]min y= min{x, y}。集合X的基数用 |X|表示。 Xy表示在将集合 X 中的对象按递增顺序排序后，对象 y的索引，例如，如果 X中的第一个对象等于 y，则 Xy= 1。 Ex表示与变量 x相关的期望。当 X为真时， 1X= 1等于1，否则为0。

2 相关工作

在文献中，能量收集与认知无线电的研究主题受到越来越多的关注。现有研究工作主要分为两类。第一类是近年来大量关于具有能量收集的无线系统的研究（赵等人， 2016；图图库卢和耶纳，2012；奥泽尔等人，2011；何和张，2012；毛等人， 2012，2014；艾哈迈德等人， 2013；毛等人，2014；Ku 等人，2015；邹等人， 2016）。赵等人（2016）、图图库卢和耶纳（2012）、奥泽尔等人（2011）、何和张（2012）以及毛等人（ 2012，2014）研究了单链路无线通信。赵等人（2016）研究了点对点通信系统中的联合无线功率与信息传输，试图在能量收集与信息传输之间实现适当的平衡，以最大化吞吐量。图图库卢和耶纳（2012）提出了一种最优传输策略，旨在有限时间范围内最大化所传输的数据量。奥泽尔等人（2011）旨在截止期限前实现最大吞吐量，并通过优化发射功率的时间序列来最小化传输完成时间。在何和张（2012）中，利用因果边信息和完全边信息，作者研究了在有限时隙范围内的能量分配问题，以最大化吞吐量。毛等人（2012）研究了感知与传输之间的能量管理问题，旨在在有限数量的时隙内最大化预期总传输数据。毛等人（2012）中考虑的能量管理问题在毛等人（2014）中被扩展至无限范围情况，通过将问题建模为无限时域马尔可夫决策过程，提出了一种最优能量分配算法。艾哈迈德等人（2013）和毛等人（2014）研究了混合能源供应系统中的资源分配问题。在艾哈迈德等人（2013）中，在有限数量的时隙内，作者研究了能量针对完成特定数量数据传输的恒定能源消耗最小化问题，毛等人（2014）研究了采用先存储后传输协议的复合能源供应网络中的最优传输调度问题。作者考虑联合分组调度与节能因子优化，以最小化电池的能耗。顾等人 （2015）通过根据信道波动和电池充电过程自适应调整传输参数，提出了一种针对太阳能供电感知节点的数据驱动解决方案，用于寻找最优策略。邹等人（2016）考虑了由双状态吉尔伯特‐艾略特马尔可夫链模型描述的间歇性能量到达场景，并为射频能量采集设备设计了最优休眠和采集策略。

其次，将认知无线电（CR）与能量收集（EH）相结合以同时提高频谱效率和能量效率，已引起广泛关注。尹等人（2015）研究了一种EH‐CR系统，其中一时隙被划分为三个非重叠部分，分别对应三种独特操作。考虑了两种融合规则，并探讨了能量采集‐感知‐吞吐量之间的权衡。在杰亚等人（2014）中，考虑到随机采集能量、信道质量和主网络的信念状态，提出了一种适用于单用户多信道环境的信道选择准则。在苏丹（2012）中，根据电池充电情况和主用户占用的信念状态，作者研究了能量管理策略，旨在实现最大吞吐量。普拉提巴等人 （2016）应用有限时域部分可观测马尔可夫决策过程来获得次用户之间在感知与接入方面的最优协作，以最大化吞吐量。在张等人（2017）中，针对异构认知无线电传感器网络，其中支持能量采集的频谱传感器协同扫描授权频谱，而数据传感器监测感兴趣区域，作者提出了一种资源分配方案，以实现频谱传感器的可持续性并节约数据传感器的能量。Park 和 Hong (2013) 以及 Park 等人 (2013) 研究了针对能量采集认知无线电网络的最优频谱接入策略，旨在在能量因果性和碰撞约束下最大化期望总吞吐量。继 Park 和 Hong (2013) 以及 Park 等人 (2013) 之后，在朴和洪（2014）中推导出可实现吞吐量的上界，其为能量到达率、主信道状态的统计行为以及检测阈值的函数。Chung等人（2014）专注于研究感知时长与感知阈值的最优配对，以最大化次级网络的平均吞吐量。在韩等人（2016）中，为了同时实现能量效率和频谱效率，研究了在能量因果性约束、碰撞约束以及感知信道概率下的能量收集与频谱感知联合优化问题。与这些工作相比，本文的显著特点是：根据当前电池能量状态、信道衰落以及收集的能量信息，我们对支持能量采集的次用户的频谱接入决策和传输功率进行联合优化，旨在最大化长期期望吞吐量。

3 网络模型

3.1 主网络模型

假设时间被划分为大小相等的时隙，用 T表示，并由 t= 1, 2,…进行索引。主用户被授权使用一个主信道，主信道的状态记为 θt ∈Θ,{0, 1}，建模为一个时齐随机过程，其中信道状态在每个时隙内随机地在占用（0）和空闲（1）之间切换，如吴等人（2012）所假设的那样。令 po, Pr(θt= 0)表示信道被主用户占用的概率。相应地，信道状态为空闲的概率表示为 pi, Pr(θt= 1) = 1 −po。我们假设次用户通过长期的频谱使用测量了解 po和 pi（Park 等人，2013；裴等人，2011）。

3.2 次级网络模型

3.2.1 机会式频谱接入与能量模型

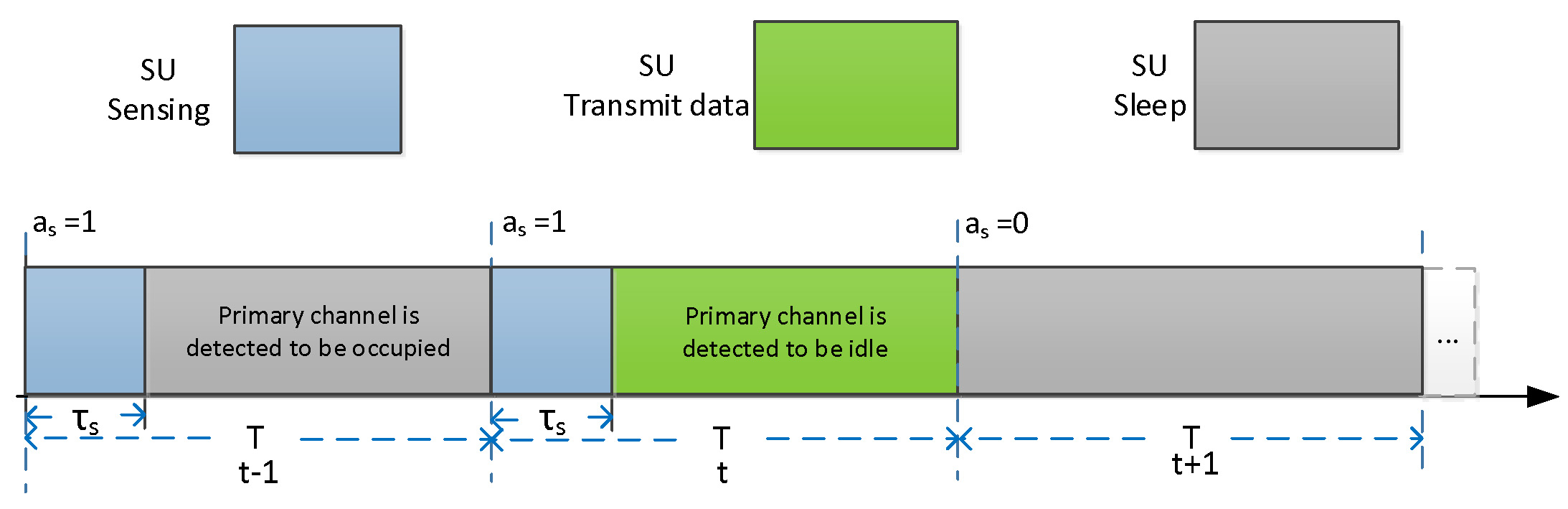
考虑一个由两个认知传感器节点组成的点对点通信链路，这些节点也称为次用户（SUs）。为了在不干扰主用户传输的情况下 opportunistic 地利用主信道，当次用户决定接入主信道时，会执行频谱感知，并在未检测到主用户信号的情况下随后进行数据传输。因此，整个传输过程包括两个阶段，即持续时间为 τs的感知阶段和持续时间为 ttr =T − τ s的传输阶段，如图1所示。当初用户未接入主信道时，次用户在整个时隙内保持睡眠模式。

我们假设次用户（SU）没有固定电源，完全依靠从周围环境收集的能量供电。以单位表示的能量到达过程 {Ht} 被假定为遵循一阶离散时间马尔可夫模型的时间相关过程，其一步转移概率由 ν hh ′, h, h ′ ∈ H给出。 H是可能收集的能量的有限集。当前时隙收集的能量将存储在具有有限容量的可充电电池中，并在下一时间槽开始时可供次用户使用（顾等人，2016）。

我们用 Et表示在时隙 t开始时存储在电池中的剩余能量（以单位计），且 Et的取值来自有限集 B,{0, 1, 2, · · · B}。剩余能量的变化规律为 Et+1= min {Et − Et,c+ Ht, B}，其中 Et,c ∈ Z+表示在时隙 t中的能耗。该能耗由次用户（SU）在时隙 t开始时做出的频谱接入决策 as ∈ As,{0(sleep), 1(active)}决定，如图1 所示。如果 as= 1（处于激活模式），SU以能耗 es= τsps进行频谱感知，其中ps为感知功率。定义感知结果为 Ox，其中 x= −1取值0、1，分别对应三种情况： O−1、睡眠、 O0、占用，以及 O1、空闲。如果主信道被检测为空闲（O1），则SU以能耗 Ed(pt)= ttrpt进行数据传输，其中 pt为传输功率。否则（O0），SU关闭所有收发器（能量采集器除外），并在传输阶段保持在睡眠模式。需要注意的是，仅当剩余能量不低于单次频谱接入所需的能量时，SU才具备执行信道感知的能力，即 Et ≥ es Park 等人 (2013)。如果 as= 0（处于睡眠模式， O−1），SU将关闭所有收发器（能量采集器除外），直到下一个时隙，并消耗可忽略的能量（朴和洪， 2013）。因此，时隙 t中的能耗表示为
$$
E_{t,c}= 1_{{E_t\geq e_s}} a_t(e_s+ 1_{O_1}E_d(p_t)).
$$

3.2.2 信道感知错误与吞吐量

通常，信道感知被认为是不完美的，频谱感知的准确性由虚警概率 P f 和检测概率 P d决定，其定义如下：
$$
P_f = \Pr{O_0 | \theta_t = 1}, \quad P_d = \Pr{O_0 | \theta_t = 0}. \tag{1}
$$
考虑到复值主信号和圆对称复高斯（CSCG）噪声的情况，根据预定义的检测概率目标值 Pd ，虚警概率由梁等人（2008）给出：
$$
P_f = Q(\sqrt{2\beta+1}Q^{-1}(P_d) +\sqrt{\tau_s f_s \beta}), \tag{2}
$$
其中 β表示次用户接收到的主信号信噪比（SNR），fs 为采样频率，且 $Q(x)=(1/\sqrt{2\pi})\int_{x}^{\infty} \exp(-t^2 /2)dt$。

令 Gt表示第 t个时隙次用户发射机到接收机的信道功率增益。假设次用户信道衰落过程{Gt}是一个时间齐次的有限状态马尔可夫链（FSMC）顾等人（2015），其一步转移概率由 ηgg′= Pr(Gt+1= g′|Gt=g) g, g′ ∈ G给出。 G是离散化信道增益的有限集。假设在每个时隙开始时，次用户能够获得 Gt的完全知晓，如吴等人（2012）中所假设。如果信道状态为 θt= 1且感知结果为 O1，则第 t个时隙的吞吐量为
$$
r(p_t, G_t)= \tau_{tr} \log\left(1+ \frac{p_t G_t}{N_0}\right), \tag{3}
$$
其中 N0是目的端的噪声功率。否则，由于次用户放弃传输（即 O0）或与主用户传输发生碰撞，我们假设时隙 t的吞吐量为零（裴等人，2011）。

本文的总体目标是通过联合优化频谱接入决策as以及传输功率，以最大化期望总吞吐量。在接下来的部分中，我们将在MDP框架内对该问题进行建模，并提出该问题。

4 问题建模

在本节中，设计框架被表述为一个马尔可夫决策过程 （MDP），旨在最大化次用户的期望总吞吐量。该 MDP主要由状态空间、动作集合、状态转移概率和奖励函数组成。由于收集的能量信息仅为因果可用，因此对于时隙 t，次用户仅知道前一时隙的收集的能量 Ht−1，故系统的状态可由一个三元组定义。
$$
s_t=(E_t, G_t, H_{t-1}) \in S= B \times G \times H. \tag{4}
$$
在时隙 t 开始时，根据系统状态 (Et, Gt, Ht−1)=(e, g, h) ∈ S，次用户首先做出频谱接入决策 as ∈ As，然后决定用于数据传输的传输功率pt。具体而言，记 P(x) 为当频谱接入决策为 x 时的传输功率动作集。 P(0)={0}，因为在睡眠模式下次用户放弃传输数据。同时， P(1)= {0,∆, 2∆, · · ·, Lmax t ∆, P max t (e)}，其中 ∆ 表示次用户传输功率的步长， L max t ∆（即 P max t (e)）表示次用户的最大传输功率。考虑到传输能耗不应超过剩余能量，我们有
$$
L_{\text{max}}^t \Delta \leq \frac{[e - e_s]^+}{t_{tr}}, \tag{5}
$$
其中[x] + = max{0, x}。本文中，我们设定 ∆=1/t tr ，对应在传输阶段消耗一个单位的能量量子，以及 L max t =[e−es] +。因此，动作集合可表示为 A={(as ,pt) |as ∈ As ,pt ∈ P(as)}

对于时隙 t，次用户根据系统状态 st 作出频谱接入决策 as 以及传输功率 pt，系统状态随后切换到新的状态st+1。从 st=(e, g, h)到 下一个系统状态 st+1=(e′, g′, h′)的状态转移概率由以下给出
$$
\Pr(s_{t+1}=(e’, g’, h’)|s_t=(e, g, h), a_s,p_t) = \nu_{hh’}\eta_{gg’} \Pr(e’|e, h’, a_s,p_t). \tag{6}
$$
给定 e, h′, as和 pt时，剩余能量 e′的条件概率函数被表述为
$$
\Pr(e’|e, h’, a_s, a_p) =
\begin{cases}
\Pr(O_{-1}), & a_s= 0, e’= \min{e+ h’, B}, \
\Pr(O_0), & a_s= 1, e’= \min{e- 1_{e\geq e_s}e_s+ h’, B}, \
\Pr(O_1), & a_s= 1, e’= \min{e- 1_{e_t\geq e_s}(e_s+ E_d(p_t))+ h’, B},
\end{cases} \tag{7}
$$
其中
$$
\Pr(O_x)=
\begin{cases}
1 & a_s= 0, x= -1, \
p_iP_f+ p_oP_d, & a_s= 1, x= 0, \
p_i(1 - P_f)+ p_o(1 - P_d), & a_s= 1, x= 1,
\end{cases} \tag{8}
$$
表示在给定频谱接入决策 as的情况下，感知结果的条件概率函数。

奖励函数定义为每个时隙中期望传输数据量。对于时隙 t，给定当前系统状态 st=(e, g, h) 和动作 at=(as,pt)，奖励函数可表示为
$$
R(s_t, a_t)=
\begin{cases}
p_i(1-P_f)\tau_{tr} \log\left(1+ \frac{p_t g}{N_0}\right), & a_s=1, e \geq e_s, \
0 & \text{otherwise}.
\end{cases} \tag{9}
$$
定义 π={π0, π1, π2, · · ·}为决策策略，其中 πt表示一个将系统状态st=(b, g, h)映射到时隙 t中规定的动作 at=(as,pt)的决策规则。本文重点关注稳态确定性策略，即决策规则在各个时隙保持不变，亦即 π={π, π, π, · · ·}。马尔可夫决策过程（MDP）的主要目标是设计最优决策策略 π∗（最优决策规则），该规则规定频谱接入决策以及传输功率，以最大化次用户的期望总吞吐量。数学上，该问题表示为
$$
\pi^* =\arg \max_{\pi} E_{\pi}\left{ \sum_{t=0}^{\infty} \lambda^t R(s_t, a_t)|s_0 \right} ,s_t \in S,a_t \in A, \tag{10}
$$
其中，期望 Eπ{·|s0}是在给定策略 π和初始状态 s 0条件下的条件期望。 0 ≤ λ< 1是折扣因子。通过调整 λ可以提供广泛的性能特性，并且通过选择接近于1的折扣因子可以很好地逼近长期平均目标（Ku 等人，2015）。

在接下来的部分中，我们首先介绍最优策略，该策略联合优化频谱接入策略和传输功率。然后，为了降低计算复杂度，将提出一种最优低复杂度策略。

5 提出的传输策略

在本节中，我们重点推导指定频谱接入决策以及传输功率相关动作的策略。首先，根据贝尔曼最优方程，我们通过在MDP中使用值迭代方法提出最优传输策略。其次，将推导一种最优低复杂度策略，以降低计算复杂度。此外，还研究了关于最优策略和低复杂度策略的结构性质。

5.1 最优策略

首先，我们证明最优策略的存在性 π∗.
定理1 ：存在一个最优的静态确定性策略 π∗ 来解决公式(10)中定义的问题。
证明 ：由于状态空间 S= B × G × H是可数的，并且对于每个系统状态 s ∈S，动作空间 A是有限的，根据(Puterman, 2005, Th. 6.2.10)，存在一个最优的平稳确定性策略 π∗。

给定任意初始系统状态 s0 ∈ S和策略 π，期望总折扣奖励（也称为价值函数）由下式给出
$$
V^\pi(s_0)= E_\pi\left{ \sum_{t=0}^{\infty} \lambda^t R(s_t, a_t)|s_0 \right}, \quad s_t \in S, a_t \in A. \tag{11}
$$
已知对于任意系统状态 s ∈ S，最优策略所达到的价值函数满足以下贝尔曼最优方程（Puterman，2005）：
$$
V^{\pi^ }(s)= \max_{a\in A}\left{R(s, a) +\lambda \sum_{i=-1,0,1} \Pr(O_i) \sum_{s’ \in S} \Pr(s’|s,a,O_i )V^{\pi^ }(s’)\right}, \tag{12}
$$
其中概率 Pr(Oi) 表示由公式 (8) 给出的观测概率。

从公式(12)可以看出，最优的预期总奖励由两部分组成：（1）当前时隙获得的即时奖励 R(s, a)；（2）关于观测概率 Pr(O i )以及更新后的系统状态的概率分布 Pr(O i , a, O i )的期望总未来奖励 $\lambda\sum_{i=-1,0,1} \Pr(O_i) \sum_{s’ \in S} \Pr(s’|s, a, O_i)V^{\pi^*}(s’)$。

在介绍最优策略的算法之前，我们首先引入函数 $V_a^{i+1}(s)$，该函数表示在第i+1次迭代时关于动作 a=(as ,pt) 的预期总奖励：
$$
V_{(1, p_t)}^{i+1}(s)= R(s, (1, p_t)) +\lambda\sum_{x=0,1} \Pr(O_x) E_{g,h}\left[V_i\left(\left[e-1_{e \geq e_s}(e_s +1_{x=1} E_d(p_t)) +h’\right] {\min B}, g’, h’\right)\right], \tag{13}
$$
and
$$
V {(0,0)}^{i+1}(s)= \lambda E_{g,h}\left[V_i\left(\left[e+ h’\right] {\min B}, g’, h’\right)\right], \tag{14}
$$
其中
$$
E {g,h}\left[V_i\left(\left[e+ h’\right] {\min B}, g’, h’\right)\right] =\sum {g’\in G} \sum_{h’\in H} \eta_{gg’}\nu_{hh’} V_k\left(\left[e+ h’\right]_{\min B},g’,h’\right). \tag{15}
$$
根据方程(13)和(14)，我们提出了通过使用值迭代方法推导最优策略的算法，如算法1所示。值迭代方法利用不动点迭代法求解具有停止准则的贝尔曼最优方程。如果我们令 ϵ→ 0，则该算法返回最优策略π∗。

在算法1中， $V_a^i(s)$ 表示在第 ith次迭代时关于动作 a的预期总奖励， Vi(s)表示在第 i次迭代时关于状态 s可实现的最大奖励。根据算法1，次用户可以迭代地寻找最优策略。具体而言，在步骤1中，对所有 s ∈ S将 V0(s) 初始化为零，并将迭代索引设为零。在步骤3中，次用户计算所有 s ∈ S的 V i( s)。然后，在步骤10中，次用户估计不等式$\max_{s \in S} |V_i(s) - V_{i-1}(s)| < \epsilon(1 - \lambda)/2\lambda$ 是否成立。如果该不等式成立，则进入步骤11以获得最优策略；否则，需要返回步骤3并执行下一次迭代。

接下来，我们研究最优策略的结构性质。首先，给出以下引理。
引理2 : 对于第 i次迭代，给定任意 g ∈ G和 h ∈ H，我们有
$$
V_i(e+1, g, h) \geq V_i(e, g, h), \quad \forall e \in B\setminus{B}.
$$
证明 ：我们通过归纳法证明此引理。根据初始条件 V0(s) = 0，可得 V1(e+1, g, h) = R(e+1, g, h, 1,[e+1−es]+/ttr ) ≥ R(e, g, h, 1,[e−es]+/ttr)= V1(e, g, h)，因为[e+1−es]+/ttr ≥[e−es]+/ttr且函数 R(·)关于 pt是非递减的。假设该命题对 i= k成立，则对于 i= k+1，当 e ≥ es且 as= 1时，我们有
$$
\max_{p_t\in P(1)} V_{(1,p_t)}(e+1, g, h) = \max_{p_t\in P(1)} R(e+ 1, g, h, 1,p_t) +\lambda\sum_{x=0,1}P(O_x)E_{g,h}\left[V_i\left(\left[e+1-1_{e\geq e_s}(e_s+1_{x=1}E_d(p_t))+h’\right] {\min B},g’,h’\right)\right] \geq \max {p_t\in P(1)} R(e, g, h, 1,p_t) +\lambda\sum_{x=0,1}P(O_x)E_{g,h}\left[V_i\left(\left[e-1_{e\geq e_s}(e_s+1_{x=1}E_d(p_t))+h’\right] {\min B},g’,h’\right)\right] = \max {p_t\in P(1)} V_{(1,p_t)}(e, g, h), \tag{16}
$$
因为相对于状态(e, g, h)的传输功率动作集，状态({v1>, g, h)的传输功率动作集提供了更多样化的动作。

此外，当 as= 0 时，我们有
$$
V_{(0,0)}^{k+1}(e+ 1, g, h)= \lambda E_{g,h}\left[V_k\left(\left[e+ 1+ h’\right] {\min B}, g’, h’\right)\right] \geq \lambda E {g,h}\left[V_k\left(\left[e+ h’\right] {\min B}, g’, h’\right)\right]= V {(0,0)}^{k+1}(e, g, h), \tag{17}
$$
因为对于 i= k， $V_k\left(\left[e+1+ h’\right] {\min B}, g’, h’\right) \geq V_k\left(\left[e+ h’\right] {\min B}, g’, h’\right)$ 成立。因此，我们证明了当 e ≥ es时， $V_{k+1}(e+1, g, h) \geq V_{k+1}(e, g, h)$。

当e ≤ es − 1时，我们有$V_{(0,0)}^{k+1}(e+1, g, h) - V_{(0,0)}^{k+1}(e, g, h) \geq 0$，其与方程(17)具有相同的形式。因此我们可以推导出 $V_{k+1}(e+1, g, h) =\max_{a\in A}{V_a^{k+1}(e+1, g, h)} \geq V_{(0,0)}^{k+1}(e+1, g, h) \geq V_{(0,0)}^{k+1}(e, g, h) = V_{k+1}(e, g, h)$。因此，我们证明了当 e ≤ es − 1时该命题也成立。于是我们得出结论： $V_a^{k+1}(e+ 1, g, h) \geq V_a^{k+1}(e, g, h)$。证明完毕。

基于引理2，我们引入以下关于最优策略的定理：
定理3 ：由最优策略获得的期望奖励随着电池可用能量的增加而非递减，即 $V^{\pi^ }(e+ 1, g, h) \geq V^{\pi^ }(e, g, h)$， e ∈ B{B}, g ∈ G,h ∈ H。
证明 ：根据引理2和值迭代算法，当算法收敛时，可推导出该定理。

从定理3可以看出，最优策略获得的期望总吞吐量随着电池中可用能量的增加而非递减。通过值迭代来驱动最优策略需要较高的计算复杂度，这通常限制了最优策略在实际场景中的应用。因此，我们在下文中引入低复杂度策略。

5.2 低复杂度策略

在本节中，我们首先介绍低复杂度策略的定义。然后进行理论分析关于最优低复杂度策略的结构性质。基于该结构性质，我们提出一种高效算法以获得最优低复杂度策略。

低复杂度策略表明，如果次用户选择睡眠模式（ as= 0），则次用户会关闭所有收发器，仅保留能量采集器。另一方面，如果次用户选择激活模式（as= 1），则次用户将忽略当前动作对未来奖励的影响，转而专注于最大化即时奖励。由于公式(19)定义的即时奖励随传输功率单调递增，因此传输功率的动作集合可表示为 P(0)={0}和 $\tilde{P}(1) ={P_{\text{max}}^t(e)=[e-e_s]^+/t_{tr}}$，其中 $\tilde{P}(x)$ 是符合频谱接入决策 x的次用户传输功率集合。相应地，低复杂度策略的动作集合退化为
$$
\tilde{A}={(a_s, a_s P_{\text{max}}^t(e))|a_s \in A_s}, \tag{18}
$$
奖励函数如下所示：
$$
\tilde{R}(s_t, a_t) =
\begin{cases}
p_i(1-P_f)\tau_{tr} \log\left(1+ \frac{P_{\text{max}}(e)g_t}{N_0}\right), & a_s=1, e\geq e_s, \
0 & \text{otherwise}.
\end{cases} \tag{19}
$$
寻找最优低复杂度策略的问题可以表述为
$$
\pi^ {\text{LC}}= \arg \max {\pi_{\text{LC}}} E_{\pi_{\text{LC}}}\left{\sum_{t=0}^{\infty} \lambda^t \tilde{R}(s_t, a_t)|s_0\right}, \quad s_t \in S,a_t \in \tilde{A}, \tag{20}
$$
where $\pi^ _{\text{LC}}$表示最优的低复杂度策略

为了推导最优策略 $\pi^* {\text{LC}}$，我们也可以根据算法1采用值迭代方法，只需通过计算 $V {a_s}^{i+1}(s)$ 和 $V_i(s)$，其中
$$
\tilde{V} {a_s}^{i+1}(s) = \tilde{R}(s, (a_s, a_s P {\text{max}}^t(e))) +\lambda\sum_{i=-1,0,1} P(O_i) \sum_{s’ \in S} P(s’|s,a_s,a_s P_{\text{max}}^t(e),O_i )V_{i-1}(s’), \tag{21}
$$
$$
\tilde{V} i(s)= \max {a_s \in A_s} {\tilde{V}_{a_s}^i(s)}, \tag{22}
$$
并将初始值 V0(s)设为零。然而，这种值迭代方法仍然需要进行大量计算。接下来，我们研究关于最优低复杂度策略的结构性质，并基于该结构性质提出一种用于推导最优低复杂度策略的高效算法。

首先，对于低复杂度情况，关于状态(e, g, h)和决策 as 的不等式(21)中的价值函数可以重写为
$$
\tilde{V} 1^{i+1}(e, g, h) = \tilde{R}(e, g, h, 1, P {\text{max}}^t(e))+ \lambda E_{g,h}\left[ \sum_{x=0,1} \Pr(O_x^t) \tilde{V} i\left(\left[1 {x=0}(e-e_s) +h’\right] {\min B}, g’, h’\right)\right], \tag{23}
$$
$$
\tilde{V}_0^{i+1}(e, g, h)= \lambda E {g,h}\left[\tilde{V} i\left(\left[e+h’\right] {\min B}, g’, h’\right)\right]. \tag{24}
$$
根据方程(23)和(24)，我们给出以下引理。
引理4 ：对于任意 g ∈ G, h ∈ H，我们有 $V_{a_s}^i(e+1, g, h) \geq V_{a_s}^i(e, g, h)$，其中 as ∈ As。
证明 ：我们通过归纳法来证明这一点。从方程(23)和(24)以及 V0(s) = 0，容易推导出 $V_{a_s}^1(e+1, g, h) \geq \tilde{V} {a_s}^1(e, g, h)$。假设该命题对 i= k成立，对于 i= k+1，当 e ≥ es时，我们有
$$
\tilde{V}_1^{k+1}(e+1, g, h)- \tilde{V}_1^{k+1}(e, g, h) = \tilde{R}(e+1, g, h, 1, P {\text{max}}^t(e+1)) - \tilde{R}(e, g, h, 1, P_{\text{max}}^t(e)) \geq 0 \quad \text{since } \tilde{R}(\cdot) \text{ is non-decreasing with } e + \lambda \Pr(O_0) E_{g,h}\left[ \tilde{V} k\left(\left[e+1 - e_s+ h’\right] {\min B}, g’, h’\right)- \tilde{V} k\left(\left[e - e_s+ h’\right] {\min B}, g’, h’\right) \geq 0 \quad \text{since the statement holds for } i=k \right], \tag{25}
$$
and
$$
\tilde{V} 0^{k+1}(e+ 1, g, h)- \tilde{V}_0^{k+1}(e, g, h) = \lambda E {g,h}\left[\tilde{V} k\left(\left[e+1+h’\right] {\min B}, g’, h’\right)-\tilde{V} k\left(\left[e+ h’\right] {\min B},g’,h’\right)\right] \geq 0 \quad \text{since the statement holds for } i=k. \tag{26}
$$
由方程(25)和(26)可得，当 e ≥ es时， $\tilde{V} {a_s}^{k+1}(e+1, g, h) \geq \tilde{V} {a_s}^{k+1}(e, g, h)$。

当e ≤ es − 1时，我们有$\tilde{V} 1^{k+1}(e + 1, g, h) =\tilde{V}_0^{k+1}(e+ 1, g, h) = \lambda E {g,h}\left[\tilde{V} k\left(\left[e+ 1+ h’\right] {\min B}, g’, h’\right)\right]$，且$\tilde{V} 1^{k+1}(e, g, h) = \tilde{V}_0^{k+1}(e, g, h) = \lambda E {g,h}\left[\tilde{V} k\left(\left[e+h’\right] {\min B}, g’, h’\right)\right]$。由于 $\tilde{V} 0^{k+1}(e+1, g, h) - \tilde{V}_0^{k+1}(e, g, h) \geq 0$与(26)具有相同的表达形式，因此当 e ≤ es −1时，我们可以推导出 $\tilde{V} {a_s}^{k+1}(e+1, g, h) \geq \tilde{V} {a_s}^{k+1}(e, g, h)$。因此我们得出结论： $\tilde{V} {a_s}^{k+1}(e+1, g, h) \geq \tilde{V}_{a_s}^{k+1}(e, g, h)$。证明完毕。

此外，我们有以下引理： 引理5 ：对于任意系统状态(e, g, h)，定义以下三个差分函数：
$$
\Theta_i(e, g, h)= \tilde{V} 1^i(e, g, h)- \tilde{V}_0^i(e, g, h), \tag{27}
$$
$$
\Lambda_0^i(e, g, h)= \Pr(O_0) E {g,h}\left[ \tilde{V} 1^i\left(\left[e+ h’\right] {\min B}, g’, h’\right) - \tilde{V} 0^i\left(\left[e-1 {e \geq e_s} e_s + h’\right] {\min B}, g’, h’\right)\right] \tag{28}
$$
$$
\Lambda_1^i(e, g, h)= \Pr(O_1) E {g,h}\left[ \tilde{V} 1^i\left(\left[e+ h’\right] {\min B}, g’, h’\right) - \tilde{V} 0^i\left(\left[h’\right] {\min B}, g’, h’\right)\right] \tag{29}
$$
函数 $\Theta_i(e, g, h)$关于 e是非递减的，如果 $\tilde{R}(e, g, h, 1, P_{\text{max}}^t(e)) -[\Lambda_0^i(e, g, h)+\Lambda_1^i(e, g, h)]$在 e ≥ e_s 时关于 e是非递减的。
证明 ：我们通过归纳法证明该引理。当 i= 1时，基于(21)、(22)和 V0(s) = 0，容易推导出Θ1(e, g, h) =R(e, g, h, 1, P_{\text{max}}^t(e))，其关于 e是非递减的。假设Θ1(e, g, h)关于 e是非递减的，对于 i= k成立。那么立即可得以下两个函数关于 e是非递减的：
$$
\Delta_{\text{max}}^k(e, g, h)= \max{0,\Theta_k(e, g, h)} \geq 0, \tag{30}
$$
$$
\Delta_{\text{min}}^k(e, g, h)= \min{0,\Theta_k(e, g, h)} \leq 0. \tag{31}
$$
当 e ≥ es 时，我们有
$$
\Theta_{k+1}(e, g, h)= \tilde{V} 1^{k+1}(e, g, h)- \tilde{V}_0^{k+1}(e, g, h) = \tilde{R}(e, g, h, 1, P {\text{max}}^t(e))+ \lambda \Pr(O_0) \cdot E_{g,h}\left[\max{\tilde{V} 1^k\left(\left[e-e_s+h’\right] {\min B},g’,h’\right), \tilde{V} 0^k\left(\left[e-e_s+h’\right] {\min B},g’,h’\right)} -\max{\tilde{V} 1^k\left(\left[e+h’\right] {\min B}, g’, h’\right), \tilde{V} 0^k\left(\left[e+h’\right] {\min B}, g’, h’\right)}\right] +\lambda \Pr(O_1) \cdot E_{g,h}\left[\max{\tilde{V} 1^k\left(\left[h’\right] {\min B}, g’, h’\right), \tilde{V} 0^k\left(\left[h’\right] {\min B}, g’, h’\right)} -\max{\tilde{V} 1^k\left(\left[e+h’\right] {\min B}, g’, h’\right), \tilde{V} 0^k\left(\left[e+h’\right] {\min B}, g’, h’\right)}\right] = \tilde{R}(e,g,h,1,P_{\text{max}}^t(e))-\lambda(\Lambda_0^k(e,g,h)+\Lambda_1^k(e,g,h))+\lambda\sum_{x=0,1}\Pr(O_x) \cdot E_{g,h}\left[\Delta_{\text{max}}^k \left(\left[1_{x=0}(e-e_s)+h’\right] {\min B},g’,h’\right)+\Delta {\text{min}}^k\left(\left[e+h’\right] {\min B},g’,h’\right)\right]. \tag{32}
$$
根据函数$\Delta {\text{max}}^k(e, g, h)$和 $\Delta_{\text{min}}^k(e, g, h)$的非递减性质，我们可以推导出Θk+1(e, g, h)在 e上保持非递减性质，如果$\tilde{R}(e, g, h, 1, P_{\text{max}}^t(e)) - \lambda(\Lambda_0^k(e, g, h) -\Lambda_1^k(e, g, h))$关于 e是非递减的。当 e< es时，由于 $\tilde{V}_1^{k+1}(e, g, h) = \tilde{V}_0^{k+1}(e, g, h)$，我们可以计算得Θk+1(e, g, h) = 0。因此这意味着该命题对 i= k+1成立。

根据引理5，接下来我们将证明对于给定的 g和 h， Θi(e, g, h)沿着电池可用能量 e的方向确实是非递减的。
定理6 ：对于任意的 g ∈ G和 h ∈ H，差分函数Θi(e, g, h)关于 e是非递减的。
证明 ：参考引理5，我们只需证明当 e ≥ es时，$\tilde{R}(e, g, h, 1, P_{\text{max}}^t(e)) -[\Lambda_0^i(e, g, h)+\Lambda_1^i(e, g, h)]$关于 e是非递减的。由方程(28)和(29)可知，当 e ≥ es时，对于 i= k ≥ 1，Φ(e) $\tilde{R}(e, g, h, 1, P_{\text{max}}^t(e)) -[\Lambda_0^i(e, g, h)+\Lambda_1^i(e, g, h)]$可分为两种可能情况，具体如下：
- Case 1 : When B − h′< e ≤ B, we have
$$
\Phi(e)= \tilde{R}(e, g, h, 1, P_{\text{max}}^t(e)) \quad \text{non-decreasing with } e +E_{g,h}\left[-\tilde{V} 1^i(B, g’, h’) + \Pr(O_0) \tilde{V}_0^i\left(\left[e- e_s + h’\right] {\min B}, g’, h’\right) \quad \text{non-decreasing with } e \text{ according to Lemma 4} + \Pr(O_1) \tilde{V} 0^i\left(\left[h’\right] {\min B}, g’, h’\right) \quad \text{a constant independent with } e \right], \tag{33}
$$
因此，可以看出Φ(e)在 B − h′ < e ≤ B时关于 e是非递减的。

• Case 2 : When es ≤ e ≤ B − h′, we have
  $$
  \Phi(e) = \tilde{R}(e, g, h, 1, P_{\text{max}}^t(e)) -E_{g,h}\left[\tilde{V} 1^i(e+h’,g’,h’) - \Pr(O_0)\tilde{V}_0^i(e - es+ h’, g’, h’) - \Pr(O_1)\tilde{V}_0^i\left(\left[h’\right] {\min B}, g’, h’\right]\right] = \tilde{R}(e, g, h, 1, P_{\text{max}}^t(e))-\mathbb{E} {g,h}\left[\tilde{R}(e+h’, g’, h’, 1, P {\text{max}}^t(e+h’)) + \lambda \mathbb{E} {g’,h’}\left[\Pr(O_1)\tilde{V} {i-1}\left(\left[h’‘\right] {\min B}, g’‘, h’‘\right) - \Pr(O_1)\tilde{V} {i-1}\left(\left[\left[h’\right] {\min B}+ h’‘\right] {\min B}, g’‘, h’‘\right)\right]\right] = \tilde{R}(e,g,h,1,P_{\text{max}}^t(e))-\mathbb{E} {g,h}\left[\tilde{R}(e+h’,g’,h’,1, P {\text{max}}^t(e+h’))\right] \quad \Upsilon(e) - \Pr(O_1)\mathbb{E} {g,h}\left[\lambda\mathbb{E} {g’,h’}\left[\tilde{V} {i-1}\left(\left[h’‘\right] {\min B}, g’‘, h’‘\right)- \tilde{V} {i-1}\left(\left[\left[h’\right] {\min B}+ h’‘\right] {\min B}, g’‘, h’‘\right) \quad \text{a constant independent with } e \right], \tag{34}
  $$
  其中 g′′表示信道状态从 g′演变而来，h′′表示到达能量从 h′演变而来。对于Υ(e)，我们可以推导出
  $$
  \Upsilon(e)= \mathbb{E} {g,h}\left[\tilde{R}(e,g,h,1,P_{\text{max}}^t(e)) -\tilde{R}(e+h’,g’,h’,1,P_{\text{max}}^t(e+h’))\right] = \mathbb{E} {g,h}\left[Q\left(\log\left(1+\frac{(e- e_s)g}{t {tr}N_0}\right) -\log\left(1+\frac{(e+ h’ - e_s)g}{t_{tr}N_0}\right)\right)\right], \tag{35}
  $$
  其中 Q= pi(1 − Pf)ttr 是一个常数。设
  $$
  \Gamma(e), \log\left(1+\frac{(e-e_s)g}{t_{tr}N_0}\right)- \log\left(1+\frac{(e+h’ - e_s)g}{t_{tr}N_0}\right), \text{we have}
  $$
  $$
  \Gamma(e)= \log\left(1+\frac{(e- e_s)g}{t_{tr}N_0}\right)- \log\left(1+\frac{(e+ h’ - e_s)g}{t_{tr}N_0}\right) = \log\left(1 - \frac{h’ g}{t_{tr}N_0+(e+ h’ - e_s)g}\right). \tag{36}
  $$
  显然， Γ(e)关于 e是非递减的。因此，函数Υ(e)关于 e是非递减的。进一步，我们可以推导出Φ(e)关于 e是非递减的当 es ≤ e ≤ B − h′.

最后，我们需要证明“情况2”下 Φ(e)的最大值不大于“情况1”下 Φ(e)的最小值，这表明在整个范围 es ≤ e ≤ B内，Φ(e)关于 e是非递减的。可以计算得到：
$$
\max_{e_s \leq e \leq B - h’} \Phi(e)=\Phi(B - h’) = \tilde{R}(B - h’, g , h, 1, P_{\text{max}}^t(B - h’)) -\mathbb{E} {g,h}\left[\tilde{V}_1^i (B, g’, h’) - \Pr(O_0) \tilde{V}_0^i (B - e_s , g’, h’) - \Pr(O_1) \tilde{V}_0^i \left(\left[h’\right] {\min B}, g’, h’\right]\right] \leq \tilde{R}(B-h’+1, g ,h,1,P_{\text{max}}^t(B-h’+1))-\mathbb{E} {g,h}\left[\tilde{V}_1^i (B, g’, h’) - \Pr(O_0) \tilde{V}_0^i \left(\left[B-e_s +1\right] {\min B}, g’, h’\right)- \Pr(O_1) \tilde{V} 0^i \left(\left[h’\right] {\min B}, g’, h’\right]\right] =\Phi(B - h’+1)= \min_{B - h’ <e \leq B} \Phi(e). \tag{37}
$$
上述方程中第四行的不等式来源于： R(e, g, h, 1, P_{\text{max}}^t(e)) 和 $\tilde{V}_0^i(e, g’, h’)$ 均为关于 e 的非递减函数，而其余所有项均为常数（与 e 无关）。因此，我们可以得出结论： 当 es ≤ e ≤ B 时，Φ(e) 关于 e 是非递减的，这足以证明 Θi(e, g, h) 关于 e 是非递减的。至此，证明完成。

定理7 : 对于任意 g ∈ G和 h ∈ H，最优的低复杂度策略 π∗ LC具有阈值结构。
证明 ：根据定理6，当值迭代算法收敛时，基于Θi(e, g, h) 的非递减性质，存在一个阈值结构Ψ={Ψ1,Ψ2, · · ·, Ψ|H|}，其中Ψl={Ψl,1,Ψl,2,…,Ψl,|G|}由以下给出
$$
\pi^* {\text{LC}}(e, g, h)=
\begin{cases}
0 & e \leq \Psi {H_h,G_g}, \
1 & e \geq \Psi_{H_h,G_g} +1,
\end{cases} \tag{38}
$$
对于满足Θi（ΨHh,Gg , g, h）的阈值ΨHh,Gg ，当 ΨGg ,Hh > 0时，有< 0和Θi（ΨHh,Gg + 1, g, h） ≥ 0；当 ΨHh,Gg = 0时，有 Θi（ΨHh,Gg +1, g, h） ≥ 0。

根据表1中的系统参数，图2描绘了阈值结构。可以看出存在阈值 Ψ={Ψ1,Ψ2,Ψ3}，其中 Ψ1={13, 8, 6, 6, 5}, Ψ2={12, 7, 6, 6, 5}, Ψ3={11,7, 6, 5, 5}，当超过这些阈值时进行数据传输，以获得最大的长期期望奖励。

根据定理7中引入的最优低复杂度策略的阈值结构，我们提出了一种高效算法来推导最优低复杂度策略，如算法2所示，该算法与算法1相比显著降低了计算复杂度。算法1和算法2之间的第一个主要区别在于，算法2中传输功率的总动作集被简化为{asP_{\text{max}}^t(e)} 。此外，算法2中计算 $\tilde{V}_i(e, g, h)$ 的过程比算法1中相应计算具有更低的复杂度。具体而言，在算法2的步骤7中，对于给定的 g和 h，当 $\tilde{V}_i(e, g, h)$ 时我们计算 $\tilde{V}_i(e, g, h)$，如果 Θi(e, g, h) ≥ 0，我们即可推断出阈值为ΨGg,Hh = 1e>0(e− 1)，并且在区间 ΨGg,Hh + 1 ≤ e ≤B内有 $\tilde{V}_i(e, g, h) = \tilde{V}_1^i(e, g, h)$。

6 数值结果

本节给出数值结果，以评估所提出策略的性能。参数值列于表1中，主要参考了毛等人（2014）；顾等人（ 2015）、杰亚等人（2014）和裴等人（2011）。能量量子的单位为0.5 mJ，电池容量为15 mJ，即 B= 30。信道功率 Gt 取自集合 G={g1 = 0.2, g2 = 1, g3 = 3, g4 = 5,