提升树模型:从提升树到GBDT树
一般来讲,提升方法实际采用加法模型与前向分步算法,以决策树为基函数的提升方法称为提升树。
提升树
提升树算法采用前向分布算法。
算法框架大致思想为:
- 首先,确定初始提升树f0(x)=0,第m步的模型是:

- 对于每一个步的模型,都是通过经验风险最小化确定模型的参数:

| 问题类型 | 损失函数 |
|---|---|
| 回归问题 | 使用平方差损失函数 |
| 分类问题 | 使用指数损失函数 |
| 一般决策问题 | 一般损失函数 |
回归问题的提升树算法流程:
假设训练集为T,训练得到提升树为fm(x)
(1) 初始化f0(x)=0
(2) 对m = 1,2,…,M
-
(i)计算残差:
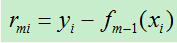
-
(ii)拟合残差rmi学习一个回归树,得到T(x;Om):
这里的拟合残差过程,利用一个CART树来进行回归学习的过程,只不过这里回归的目标不再是原来的标签,而是上个树模型回归后的残差。(比如,回归年龄50岁,上个树回归预测23岁,那么这次的残差就是50-23=27岁,回归的过程参考CART)
-
(iii)更新以下提升树:
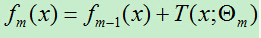
(3)得到回归树:
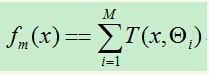
GBDT树
在提升树算法中,当损失函数是平方损失和指数损失函数时,每一步的优化都比较简单,但对于一般损失函数而言,就不容易处理。
因此,GBDT首先使用最速下降的近似方法来计算残差的近似值:
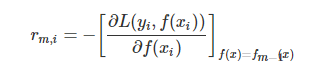
参考博客:子龙风已经总结的十分好了,在这里就不重复书写。

GDBT正则化:
- 第一种是和Adaboost类似的正则化项,即使用步长(learning rate),定义为 α
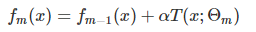
- 子采样比例(subsample),取值为(0,1]。注意这里的子采样和随机森林不一样,随机森林使用的是放回抽样,而这里是不放回抽样。如果取值为1,则全部样本都使用,等于没有使用子采样。如果取值小于1,则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差,即防止过拟合,但是会增加样本拟合的偏差,因此取值不能太低。推荐在[0.5, 0.8]之间。
使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。由于使用了子采样,程序可以通过采样分发到不同的任务去做boosting的迭代过程,最后形成新树,从而减少弱学习器难以并行学习的弱点。 - Regularized Learning Objective,将树模型的复杂度作为正则项显式地加进优化目标里
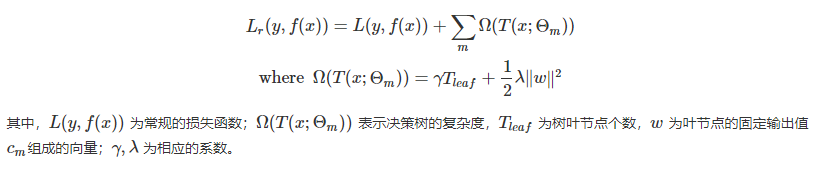





 本文介绍了提升树模型的概念,特别是关注于GBDT树。提升树算法采用前向分布算法,以决策树为基函数。在每一步中,通过经验风险最小化确定模型参数,用CART树拟合残差。GBDT在处理平方损失和指数损失函数时优化简单,但对一般损失函数处理较复杂,采用最速下降的近似方法。正则化包括步长和子采样,子采样有助于防止过拟合。
本文介绍了提升树模型的概念,特别是关注于GBDT树。提升树算法采用前向分布算法,以决策树为基函数。在每一步中,通过经验风险最小化确定模型参数,用CART树拟合残差。GBDT在处理平方损失和指数损失函数时优化简单,但对一般损失函数处理较复杂,采用最速下降的近似方法。正则化包括步长和子采样,子采样有助于防止过拟合。
















 997
997

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








