清晰易懂的马尔科夫链原理介绍

马尔科夫链是一种非常常见且相对简单的统计随机过程，从文本生成到金融建模，它们在许多不同领域都得到了应用。马尔科夫链在概念上非常直观且易于实现，因为它们不需要使用任何高级的数学概念，是一种概率建模和数据分析的经典方法。

1. 马尔科夫链场景分析

首先，我将用一个非常常见的例子来描述它们：

 

假设有两种可能的天气状态：晴天或阴天，你随时都可以观测当前的天气状态且状态限定为晴天或阴天。

 

现在你想预测明天的天气情况，你本能的会认为当天的天气会对明天的天气有一定的影响，因此，拥有智慧和才貌的你会收集并分析过去几年的天气数据，发现了一个规律——当天是阴天第二天是晴天的概率为0.25，由于天气限定为晴天或阴天，那么当天是阴天第二天也是阴天的概率为0.75。

 

因此你可以基于当前的天气状态去预测未来几天的天气。

 

这一例子阐述了马尔科夫链的关键概念：马尔科夫链本质上是由满足马尔科夫性质的转移概率分布组成，下图为天气例子的转移概率：

马尔科夫的性质在于它的无记忆性，下一时刻的状态只与当前的状态相关。用数学公式描述为：

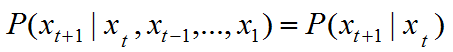
其中是时间状态序列。

这个例子介绍了如何仅通过观察当天到下一天的转移来获得概率分布，这说明了马尔科夫的性质在于它的无记忆性。

 

马尔科夫的无记忆性通常使它们无法成功预测某些潜在会发生的趋势，比如马尔科夫链可能根据词频模仿作者的写作风格，但它无法产生具有深刻主题意义的文本，因为这种主题是基于更长的文本序列产生的，马尔科夫链只考虑当前的状态，不考虑之前状态的信息。

2.马尔科夫链模型分析

马尔科夫链是通过状态转移的概率分布体现的，称为马尔科夫链的转移矩阵。如果马尔科夫链有N个可能的状态，则转移矩阵的大小是N阶，矩阵的项（i,j）是状态i到状态j的转移概率，另外矩阵的每一行的转移概率和等于1，表示状态i的概率分布。

如下图的马尔科夫链，状态用圆表示，边表示状态的转移概率。

相应马尔科夫链的转移矩阵为：

马尔科夫链也包含了每个状态的初始概率，称为马尔科夫链的初始状态向量，向量的大小与状态数相等，如下图的初始状态向量：

状态转移分布和状态的初始分布是马尔科夫链的两个基本属性。

3.马尔科夫链性质分析

上节介绍了马尔科夫的两个基本属性是状态转移分布和状态的初始分布，本节用上一节的状态转移矩阵例子来分析马尔科夫链的性质。

假设初始状态为：

初始状态经过第一次状态转移后的状态分布为：

第二次状态转移后的状态分布为：

第三次状态转移后的状态分布为：

第n次状态转移后的状态分布为：

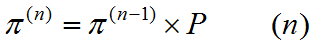
编码状态转移过程并输出结果，可知经过多次转移状态转换后，状态的分布收敛于稳定的概率分布：

假设初始状态为：

由上面结果可知经过多次状态转移后，状态的分布收敛于稳定的概率分布：

因此状态分布的收敛性与初始状态的分布无关，经过多次状态转移后，状态趋于平稳分布，方程式表示如下：

状态分布收敛于稳定的概率分布称为状态平稳分布，状态的平稳分布与初始状态分布无关，也可说当状态转移确定后，马尔科夫模型也已经确定了。

结合（1）式（2）式...（n）式，得到状态分布与状态转移的关系：

由上式可知，我们也可以从从状态转移矩阵的多次状态转换来分析模型的收敛性。

由上面结果可知：状态转移矩阵经过多次状态转换后，模型开始收敛且收敛后的状态转移分布与状态转移前的状态无关，如上一个状态为牛市、熊市或横盘，状态转移结果为熊市的概率都为0.625，也就是说多次状态转换后，熊市的状态分布稳定在0.625。

4.马尔科夫链收敛条件

马尔科夫链模型是否收敛取决于状态转移矩阵，当状态分布和状态转移矩阵P满足：

则称马尔科夫链收敛，其中为状态i转移到状态j的概率。

证明：

当时，就得到如下等式：

上式的含义等价于马尔科夫链收敛于稳定的状态分布。

另外我们对转移矩阵也有一些限制：

（1）马尔科夫链的状态转换不是循环的，如果循环则永远不会收敛，简单点说就是非周期性

的马尔科夫链才会收敛，实际应用中马尔科夫链一般都是非周期性的。

周期性的马尔科夫链如下：

状态i -> 状态j -> 状态k -> 状态i -> 状态j -> 状态k ->.....状态i -> 状态j -> 状态k

则该马尔科夫链不会收敛。

（2）任何两个状态是连通的，即状态转移矩阵没有为0的项。

（3）状态数是有限的

（4）状态间的转移概率需要固定不变。

5.小结

本文介绍了马尔科夫链的基本知识，马尔科夫链的收敛性使我们可以用马尔科夫链采样得到我们需要的样本集，马尔科夫链的无记忆性是隐马尔可夫模型和条件随机场的理论基础，后续会写相关的内容，请持续关注小编吧！

推荐阅读

520 页机器学习笔记！图文并茂可能更适合你，文末附下载方法

李航老师《统计学习方法》(第2版）课件分享，文末附下载

Github | 吴恩达新书《Machine Learning Yearning》完整中文版开源

经典好书 | 141页的《Deep Learning with PyTorch》开源书籍

欢迎扫码关注：