#21557.
洛特卡-沃尔泰拉模型（Lotka-Volterra model）
-
洛特卡-沃尔泰拉模型也称猎食模型，它由方程
表示。式中常数k 1、k 2、k 3和k 4分别表示被食者总数增长速率、被食者遭遇猎食者后的死亡速率、猎食者总数增长速率和猎食死亡速率。
#21558.
状态向量（state vector）
- 一个动态系统的状态是以一组彼此线性独立的变量来表示的，由这些变量构成的向量称为状态向量。
#21559.
状态空间（state space）
- 由状态向量所张的空间称为状态空间。
#21560.
状态方程（state equation）
-
设x
1，x
2，…，x
n（连续情形）和x
1(k)，x
2(k)，…，x
n(k)（离散情形）是状态变量，由状态可以构成状态方程。一阶微分方程组
┆
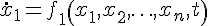
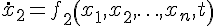
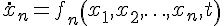
或一阶差分方程组（k是采样节拍）
x 1(k+1)=f 1[x 1(k),x 2(k),…,x 1(k),k]
x 2(k+1)=f 2[x 1(k),x 2(k),…,x 1(k),k]
┆
x n(k+1)=f n[x 1(k),x 2(k),…,x n(k),k]
称为非自治状态方程组。若方程组中不显含t或k，则方程组是自治的。这些方程组可以写成向量形式：
x(k+1)= f[ x(k),k]
#21561.
相平面（phase plane）
- 二维状态空间特称相平面。
#21562.
平衡点（equilibrium point）
-
在状态空间中，速度场为零的点叫做平衡点。在相平面中，由平衡点的本征方程λ
2+δλ+k=0的两个根
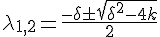的性质可以决定平衡点的分类。式中
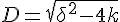叫做判别式。
#21563.
结点（node）
- 判别式D＞0的平衡点称为结点。D＞0，λ 1≠λ 2对应寻常结点，D=0，λ 1=λ 2对应内弯结点。δ＞0表示正阻尼，λ 1,λ 2＜0该结点稳定；δ＜0表示负阻尼，λ 1,λ 2＞0该结点不稳定。结点的相轨迹呈扭曲状。
#21564.
焦点（focus point）
- 判别式D＜0的平衡点称为焦点。δ＞0，该焦点稳定；δ＜0，该焦点不稳定。焦点的相轨迹呈螺旋形。一个衰减振荡的单摆，最后会停止摆动（速度场为零），静止在一点，该点就是它的平衡点——稳定焦点。
- #21565. 鞍点（saddle）
- 对应k＜0的平衡点称为鞍点。鞍点不稳定，其相轨迹呈马鞍形，在相平面上有四条轨迹，它们有两条渐近线。鞍点是一种重要的平衡点，其渐近线有流入（稳定支）和流出（不稳定支），它们可以构成分界。例如当一个单摆的初始位置达到180°时，它摆动的方向并不确定，该点是不稳定的平衡点——鞍点。
#21566. 中心点（center）-
D＜0，δ=0的平衡点称为中心点。中心点的相轨迹是椭圆，它的结构是不稳定的，只要稍有阻尼（正或负），中心点就变为焦点（稳定或不稳定）。一个理想单摆与垂直线夹角为零的点就是中心点。它在无阻尼状态下，永远摆动，只要稍有阻尼，最终会停止摆动。
又如冷等离子体振荡，在略去电子压力和磁场的情形下，把电场写成势的梯度，且考虑行波解，可以得到冷等离子体振荡的运动积分，它的相图是一族椭圆（图b），图中横轴上的H=-2ω 02的点就是中心点（ω 0是冷等离子体振荡的圆频率，H是哈密顿量）。图(c)是冷等离子体振荡电子平均速率与时间的关系。
#21567. 映射（map）- 假定X是一个集合，如果对每个x∈X作为第一坐标，都有一个且只有一个y与x结成有序对〈x,y〉，其第二坐标y的全体记为集合Y，则所有这种有序对的全体是一个集合f，这时称f为把X变到Y上的映射，记为Y=f(X)。简单地说，映射就是变换。
#21568. 同胚（homeomorphism）- f和f -1都是连续的双射称为同胚。
#21569. 微分同胚（diffeomorphism）- 若一同胚是C n（可微分至n次）的，则称之为微分同胚。
#21570. 流形（manifold）- 一个n维流形M是一个豪斯多夫空间。豪斯多夫空间是一个拓扑空间，使任意两个分开的点有分开的邻域，使每个点有一个开邻域N同胚于E n（度规欧几里得空间）的一个开集U i，即h:N i→U i。局部欧几里得拓扑空间一般叫做拓扑流形。
#21571. 庞加莱映射（Poincaré map）- 设状态轨迹横截性穿过流形S 0和S 1，令q 0和q 1是轨迹于时刻t 0和t 1与流形S 0和S 1的两个交点，则映射P(q):S 0→S 1就称为庞加莱映射。
#21572. 庞加莱首次返回映射（Poincaré first return map）- S 0和S 1是同一个流形时的庞加莱映射叫做庞加莱首次返回映射。
#21573. 伯克霍夫抽象动力学（Birkhoff abstract dynamics）- 这是一种对动力学的抽象研究，它并不去解方程，而是把动力学系统考虑成一个微分同胚。在抽象的级别上，不再有微分方程，也不再有与之相关联的状态空间。例如：光滑流形M上定义了一个测度μ，又定义f t:M→M为保测度微分同胚的一个单参数群，则M，μ，f t就称为一个经典动力学系统。
#21574. 流（flow）-
流也叫相流，定义于R
n上。
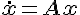的解是
x=e
At
x
0，e
At:R
n→R
n定义了R
n上的一个流，它包含了微分方程
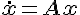所有解的集合。
- #21575. 中心流形（center manifold）
-
切于中心本征空间的不断流形W
C(0)叫中心流形。一般求法如下：设系统可分为稳定部分
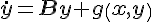和中心部分
，其中
x,y∈R
C×R
S，
A∈R
C×R
C，
B∈R
C×R
S，f(0,0)、g(0,0)、
Jf(0,0)、
Jg(0,0)均等于0，方程
的不动点是中心流形和中心空间相切的点。在中心流形W
C(0)上任一点的坐标必须满足关系
y=
h(x)，它对时间求导：
。在中心流形上的任一点，必须可代入
y与
x和
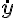与
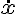满足的关系，于是得到：
J[ h(x)]{ Ax+f[ x,h(x)]}
= Bh(x)+g[ x,h(x)]
解出 h(x)。
#21576. 李雅普诺夫意义中的稳定性（stability in the sense of Liapunov）- 设一系统存在平衡状态 x e，在t 0时刻稳定，则必须满足条件：对每个ε＞0，存在δ(t 0,ε)＞0，使欧几里得范数|| x(t 0)- x e||＜δ(t 0,ε)→|| x(t)- x e||＜ε,t＞t 0，则称此平衡状态满足李雅普诺夫意义中的稳定性。例如一个理想单摆，它的摆动永远不会停止，它在李雅普诺夫意义中是稳定的，但不是一致稳定，也不是一致渐近稳定。
#21577. 一致稳定（uniformly stable）- 若满足|| x(t 1- x e)||＜δ(ε),t 1≥t 0→|| x(t)- x e||＜ε,t≥t 1，则称 x e在(t 0,∞)上一致稳定。
#21578. 一致渐近稳定（uniformly asymptotically stable）- 若δ 1＞0，满足|| x(t 1)- x e||＜δ 1,t 1≥t 0→|| x(t)- x e||→0,t→∞则称 x e在(t 1,∞)上一致渐近稳定。例如，一个有耗单摆最终会停止摆动，它是一致渐近稳定的。
#21579. 平衡点的稳定性（stability of equilibrium point）- 平衡点的稳定性是指系统受微扰后是否能回到该平衡点，若是，由该平衡点是稳定的，否则是不稳定的。
#21580. 结构稳定性（structure stability）- 结构稳定性是指状态轨迹的结构是否变动。在系统状态方程上加一小量以微扰整个向量场，使得流在拓扑上和初始的流等效，则此系统在结构上是稳定的。
#21581. 近似方法（approximation methods）- 非线性问题很难得到解析解，通常要用近似方法来逼近真正的解。常用的近似方法有两种。一是平均法，也称KBM方法（可用于自治系统和非自治系统），方法是在对非线性作用的情况下将振荡幅度和相位对时间的导数对相位求平均，从而得到振荡幅度和相位对时间的关系。二是迭代法，也就是逐步逼近的方法，例如：差分方程x n+1=a-x n2，先设定一个初始值x 0=b，代入差分方程得到x 1=a-b 2，再将该值代入上述方程，得到x 2=a-a 2+2ab 2-b 4，再代x 2入原方程……，当n→∞时，就得到真正的解。
#21582. 莫尔斯函数（Morse function）-
莫尔斯函数是一种任意标量函数：M(
x):R
n→R
1，如果在某点存在
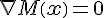，则在该点满足
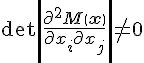
例如M=±x 12±x 22±…±x n2是莫尔斯函数，而M=-x 13-x 22非莫尔斯函数。大多数准极值函数是莫尔斯函数。
#21583. 基本突变集（elementary catastrophe set）-
梯度系统
，
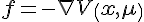x∈
R
n，
μ∈R
k，若
f(
x,μ)=0有解，则必须满足
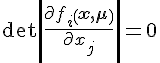。满足条件
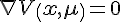和
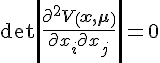的集合称为控制空间中的基本突变集。
#21584. 汤姆突变理论（Thom's catastrophe theory）- 大多数光滑函数（无限次可微）V( x,μ)[ x∈R n, μ∈R k,k＜5]结构是稳定的。对该族（V:R n×R k→R 1），任意点( x,μ)∈R n×R k对 μ∈R k， x∈R n有一种坐标选择，使x i随 μ光滑地改变。函数V( x,μ)通常可为常数加如下函数之一：x 1；莫尔斯函数；折叠突变集；叉式突变集（+）和双叉式突变集（-）；双曲脐（-）和椭圆脐（+）；抛物（和双抛物）脐；第二双曲脐（-）和第二椭圆脐（+）；符号（双符号）脐。
- #21585. 局部分岔（local bifurcation）
- 在退化平衡点（分岔）或闭轨道（分岔）附近研究向量场，并作分岔分析，该分岔能在此极限集邻域内找到，这种分岔叫局部分岔。这时，平衡点的本征值的实部随着控制参数的变化而等于零，分岔产生。例如：鞍-结分岔、跨临界分岔、尖拐分岔、霍普夫分岔。
#21586. 鞍-结分岔（saddle-node bifurcation）-
系统
的平衡点在μ=0处发生分岔，x=0，y=0的点是分岔点。分岔结果得到鞍点结点对，这种分岔叫鞍-结分岔，也叫折叠分岔。控制参数由大于零向零变化时，鞍点和结点相互靠近，在μ=0时相遇而湮没。
#21587. 跨临界分岔（transcritical bifurcation）-
系统
的平衡点有两个，一个是鞍点，一个是结点。在控制参数由小到大变化时，该两平衡点会相互靠近，当μ=0时发生分岔，两平衡点相遇而湮没。μ一旦大于零，又出现了鞍点和结点。从现象上看它们跨过了分岔点，所以称为跨临界分岔。
#21588. 尖拐分岔（cusp bifurcation）-
系统
在μ＜0时只有一个平衡点：原点，它是稳定的结点。当μ=0时，发生分岔，原点变为不稳定的鞍点，而另外产生一对稳定的结点（位置对称于原点），在控制-相空间图上控制-相轨迹犹如双尖，因而称为尖拐分岔。
#21589. 霍普夫分岔（Hopf bifurcation）-
系统
的原点是平衡点。本征值是
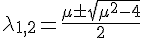。当μ=0时，发生分岔，原点由稳定的焦点变成中心点，而后又变为不稳定的焦点，且产生一围绕原点的稳定的极限环。这种分岔称为霍普夫分岔。
#21590. 倍周期分岔（period-doubling bifurcation）- 倍周期分岔是一种环的局部分岔，随着非线性运动方程控制参数的改变，一个极限环丧失了它的稳定性而出现了另一条闭轨道，其周期是原来那条闭轨道的两倍（2T），当控制参数继续增加时，该闭轨道的稳定性会减弱而直至变得不稳定，于是又有一条稳定的倍周期轨道出现，其周期为原始轨道的四倍（4T）…。在一些物理问题中可以观察到一系列n倍周期分岔，最后得到周期为2 nT的稳定极限环。若n→∞，则产生混沌。
#21591. 切分岔（tangential bifurcation）- 迭代映射在与45°线相切处产生的分岔称为切分岔。在切点附近要经过很多次迭代才能通过。
#21592. 菲根鲍姆普适数（Feigenbaum universal number）-
在迭代映射x
i+1=F(x
i,μ)的倍周期分岔的控制-相图中，分岔有自相似结构：两个周期点被一个超稳定参数（斜率
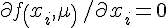对应的不动点叫超稳定点，对应的控制参数叫超稳定参数）隔开，这些自相似结构有不变的标度因子。在超稳定参数上，相邻两分岔的相空间标度比是α
i=l
i/l
i+1，当i→∞时，α
∞=2.502907875…。对应的相邻两控制参数差值比是：
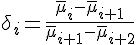，当i→∞时，δ
∞=4.6692016…。α
∞和δ
∞称为菲根鲍姆普适数。
#21593. 泛函重整化群方程（functional renormalization group equation）-
一个倍周期过程，可以把函数F(i,μ,x)=f{μ,f[μ,…,f(μ,x)]}≡f·f·…·f(μ,x)变成合成函数F·F，然后移动参数，把它从当前的超稳定值μ
i变到下一个超稳定值μ
i+1，再把标度因子α反过来：函数F→-αF·F，其宗量x→-x/α。于是得到一个变换的极限式：
g(x)
=-αg[g(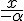
)]
这就是菲根鲍姆泛函重整化群方程。
#21594. U序列（U sequence）- 一个倍周期序列，每个周期有一个振荡，在周期倍增后，会有它自己的无限倍周期序列2 n。对自然数K，若每个周期有K个振荡，它们都有自己的无限倍周期序列2 nK，这种序列叫做U序列。
- #21595. 沙尔科夫斯基序列（Sharkovskii sequence）
- 3→5→7→9→…→2×3→2×5→2×7→2×9→…→2 n×3→2 n×5→2 n×7→2 n×9→…→2 n→…→8→4→2→1称为沙尔科夫斯基序列，用它可以预测周期的次序。使用规则：当有几个相同周期的事件发生时，只有第一个事件会出现在序列中。
#21596. 大范围分岔（global bifurcation）- 平衡点或闭轨道的稳定流形和不稳定流形间没有横截性所表征的分岔叫大范围分岔。例如同宿分岔、异宿分岔。
#21597. 同宿分岔（homoclinic bifurcation）- 鞍型平衡点自身的“流出”和“流入”间形成的分岔叫同宿分岔，它属于大范围分岔。
#21598. 异宿分岔（heteroclinic bifurcation）- 鞍型平衡点之间的“流出”和“流入”间形成的分岔叫异宿分岔，它也属于大范围分岔。
#21599. 梅尔尼科夫判据（Melnikov criterion）-
梅尔尼科夫判据是一种判定同宿分岔是否存在的判据。由距离函数
Δ ε(θ 0,θ 0)=ε∫ -∞∞ f 0[ x 0(t-θ 0)]
∧ f 1[ x 0(t-θ 0),t]dt
构成梅尔尼科夫函数
M(θ 0)=∫ -∞∞ f 0[ x 0(t-θ 0)]
∧ f 1[ x 0(t-θ 0),t]dt
可以得到同宿分岔存在的条件：若存在足够小的ε＞0，梅尔尼科夫函数有单零点，则对某个θ 0∈[0,2π]，如果流形W U( x * ε,θ0)和流形W S( x * ε,θ0)横截性相交，横截性同宿轨道存在。
#21600. 符号动力学（symbol dynamics）- 符号动力学是一种粗线条描述方法，它用有限精度对动力学过程进行严格描述，得到结果。
#21601. 迭代映射（iteration map）- 离散时间系统x i+1=F(x i)，这是一种迭代映射关系，点x i+1就是点x i的映象。
#21602. 不动点（fixed point）- 满足 x=F( x)的点称为不动点。
#21603. 不动点映射（fixed point map）- x f=F(x f)称为不动点映射，式中x f是系统x i+1=F(x i)的不动点。
#21604. 奈马克映射（Neimark map）-
奈马克映射是一种二维映射：
，线性化后不动点的本征值位于Z平面上。平面上的单位圆是不动点稳定与否的本征值的边界。由本征方程λ
2-(a+d)λ+ad-bc=λ
2-Tλ+D=0，得到本征值
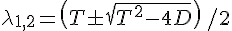，可以定出在T-D平面上本征值使不动点稳定的条件：三条直线D=1，T+D=-1，T-D=1所围的三角形。
- #21605. 埃农映射（Hénon map）
- `{[x_{x+1}=y_i+1-/mu x_i^2],[y_{i+1}=/eta x_i]:}`称为埃农映射，它有两个不动点：$x_{f_{1,2}}=/frac{/eta-1/pm sqrt{(/eta-1)^2+4/eta}}{2/mu}$，y f1,2=ηx f1,2。该映射在一定的参数条件下会出现周期轨道，也会出现混沌。
#21606. 逻辑斯蒂映射（logistic mapping）- x i+1=μx i(1-x i)称为逻辑斯蒂映射，在群体生物学中，用作种群数量模型（也叫虫口模型或宏观经济模型）。x i代表某个种群第i代的总数量，且用该种群最大数量来归一化。这种映射在拓扑上属于单峰映射。
#21607. 平方映射（square mapping）- x i+1=1-μx i2称为平方映射，它是一维映射，由埃农映射在η=0时得到，它也是一种单峰映射。
#21608. 斯梅尔映射（Smale map）- 斯梅尔映射是一种二维迭代映射，也称马蹄映射。它不产生混沌，而是一种混沌前的过渡。映射方法如下：作一正方形S，将其纵向伸展μ(＞2)倍，横向伸展η(＜2)倍，然后弯成竖向马蹄状，再与原正方形叠合，该叠合部分有两条纵向的阴影，这是一次正映射。按此做法，可得2 n条纵向的阴影，这是n次正映射。若将原正方形纵向压缩μ(＞2)倍，横向压缩η(＜1/2)倍，然后弯成横向马蹄状，再与原正方形叠合，该叠合部分有两条横向的阴影，这是一次逆映射。同理可得n次逆映射。把上述两种结构叠合起来，就得到正方形S内的不变集：`I=I^{+}/bigcap I^{-}=/bigcap_{i=-oo}^oo f^i(S)`。
#21609. 圆映射（circle mapping）- `/varphi_{i+1}=/varphi_i+/frac{K}{2/pi}sin(2/pi/varphi_i)+/omega`称为圆映射，它对角度呈周期性，参数K和ω是受迫振荡的幅度和频率。
#21610. 标准映射（standard mapping）-
标准映射可以作为一种原型来研究保守系统中从规则运动到混沌系统的过渡，映射方程：
J n+1=J n+Ksinθ n
θ n+1=θ n+J n+Ksinθ n
式中K＞0，J和θ称为作用和角度变量。不动点是J=2mπ和θ=0，π(m=0,±1,…)，对每个m，都有两个不动点：θ +和θ -。
#21611. 茹利亚集（Joulia set）- 复数逻辑斯帝映射z i+1=z i2+C，对固定的复控制参数，所有的i都有界的相空间内点集的边界称为茹利亚集。
#21612. 芒德波罗集（Mandelbrot set）- 在茹利亚集中，将复控制参数在控制空间中形成的点集{C R,C I}叫做芒德波罗集。它是一个连通集，结构非常复杂。可以用复数逻辑斯蒂映射z i+1=z i2+C，由z 0=0开始，取C值进行迭代，凡收敛者均以黑式表示，于是得到芒德波罗集的图形。
#21613. 混沌运动（chaos movement）- 混沌是一种运动状态，是在确定性系统中出现的无规性，其主要特征是动力学特性对初始条件的依赖性非常敏感。一个混沌系统既是确定的又是不可预测的，也不能分解为两个子系统。
#21614. 混沌吸引子（chaos attractor）- 也称奇异吸引子。它具有分形性质。
- #21615. 伯克霍夫-肖混沌吸引子（Brikhoff-Shaw chaos attractor）
- 由含有非线性阻尼和非线性恢复力的二阶非线性受迫运动方程，可以得到伯克霍夫-肖混沌吸引子，它的特点是吸引子表面“支离破碎”，有不能同时消失的“侧翼”，表面维数非整数，大于2而小于3。在庞加莱截面上，当控制参数改变时，吸引子会发生不可捉摸（blue sky）突变。
#21616. 勒斯勒尔混沌吸引子（Rössler chaos attractor）-
由勒斯勒尔方程
可得勒斯勒尔混沌吸引子。这是一个带状吸引子，它由两个鞍型螺旋平衡点构成。控制参数c起非线性折叠效应“开关”的阈值作用，使一个螺旋的“流出”成为另一个螺旋的“流入”，在适当的参数值时，产生多种带状混沌吸引子。折叠效应使相轨迹层层相叠（不重合）。
#21617. 洛伦兹混沌吸引子（Lorenz chaos attractor）-
根据洛伦兹方程
可作出洛伦兹混沌吸引子。b是所研究流体的形状参数，r是相对瑞利数，σ乃普兰德尔数。当固定b和σ而改变r由小于1经过1时，流体由热传导变为热对流，平衡点由一个（原点，稳定结型点）变为三个（原点变为鞍型点，另外两个是对称的稳定结型点）。随着相对瑞利数的增大，稳定的结型点变为稳定的焦型点，接着产生同宿分岔、异宿分岔、霍普夫分岔，两稳定的焦型平衡点变为不稳定的螺旋型鞍点，状态轨迹在三个不稳定的平衡点之间运动，形成洛伦兹混沌吸引子。这时流体呈湍流运动状态，相轨迹也是层层相叠。
#21618. 不可捉摸突变（blue sky catastrophe）- 当混沌吸引子A分岔出另一吸引子B时，在同一控制阈值，B突然出现而A消失，B可以存在下去，或者根本不存在，不论那种情形，分岔总是以吸引子A的消失而出现，这种突变叫不可捉摸突变，含有不可思议、意外的意思，它仅发生于微分方程的混沌吸引子。
#21619. 量子混沌（quantum chaos）-
在量子力学中，系统状态一般用波函数和能量本征值来描述，因而在研究初始条件微扰的敏感性概念等问题时，希望用波函数和能量本征值的一些特征来区别规则运动和混沌运动。诸如此类的问题，有时不作严格的系统论述，归之于量子混沌。令
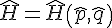是系统的哈密顿，它的经典极限是H=H(p,q)。经典极限哈密顿H所给出的动态混沌意味着哈密顿
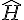的量子性质。
#21620. KAM定理（Kolmogorov-Arnold-Moser theorem）-
令Q是R
n的开集，H
1(
J,
θ,ε)乃对所有
J∈Q，0≤θ
i≤2π的(
J,
θ,ε)实解析函数，且对每个θ
1,…,θ
N有周期2π，且ε接近于零；H
0(
J)≡H(
J,
θ,0)独立于
θ；若对
J∈Q有
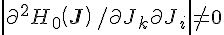
相应的频率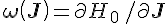
对所有的向量|
k|=|k
1|+…+|k
N|≥1满足|
k·ω|≥C|
k|
-M，则对足够小的ε，近可积系统的哈密顿表示
H=H 0( J)+εH 1( J, θ) ( J, θ∈R N)
在 θ′= θ+ f( θ,ε)和 J′= J+ g( θ,ε)定义的“不变环面”上有解。 f和 g乃对每个θ 1,…,θ N有周期2π的ε和θ的实解析函数，且在ε=0时为零。在这些环面上，满足
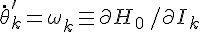(k=1,…,N)
当ε→0时，几乎对所有的频率，微扰系统的不变环面存在，并靠近未受微扰系统的不变环面。
#21621. 分形（fractal）- 分形是一集合，其豪斯多夫维严格超过拓扑维。拓扑维总是整数，豪斯多夫维可能有非整数。
#21622. 豪斯多夫维（Hausdorff dimension）-
令
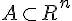，σ是半径为r
1，r
2，…的可数球的覆盖，它们满足0＜r
n＜δ/2，令d＞0，对不同的覆盖δ考虑和总∑r
nd，Inf∑r
nd表示对所有满足上述条件的总和采用的最小值（总和的最大低限）。在极限δ→0时，若d＜D
H，总和将发散，d＞D
H，总和将为零，而d=D
H（D
H不一定是整数），极限将存在。D
H称为集合A的豪斯多夫维（也称分形维）。
#21623. 盒维（box dimension）- 用可数的边长为δ的小立方体（也称盒子）覆盖集合，计算盖满集合的最少盒子数（该数值乃盒子大小的函数），由此来渐近盒子数目N(δ)的极限aδ -DB（a为某个常数），其中的D B叫盒维。
#21624. 关联维（correlation dimension）-
用数据构成一维数足够高的m维空间（叫做嵌入空间），使吸引子在其中，且不受约束，然后选定时间延迟τ=pΔτ（p为整数），形成m维向量集合，其分量取自序列z
i=(x
i,x
i+p,…,x
i+(m-1)p)，i=1,2,…，取M个向量（一般M＜N，N足够大），测量两个向量间的距离（距离定义采用：
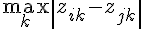，k=1,2,…,m，即相应分量的最大距离决定了两向量的距离）。如果该距离小于预置数ε，则说此两向量关联，否则不关联。计数M个向量中关联的对数，并用M
2标称化：
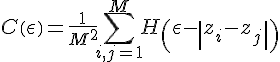
（H(x)是亥维赛德函数），于是定义关联维：
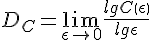
- #21625. 信息维（information dimension）
-
令覆盖奇异集的非空盒（即小立方块）的总数为N(δ)，而N
i(δ)是第i种盒子的数目，因而这种盒子的概率就是P
i(δ)=N
i(δ)/N(δ)。取对数测度
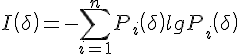，于是得到信息维：
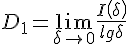
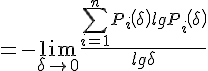
#21626. 分形布朗运动（fractal Brownian movement）- 在自然界中，分子、大分子、病毒、粒子等都由于热涨落而以随机碰撞的形式不停地运动，这种运动称为布朗运动。布朗运动的粒子位置是时间的随机函数，对归一化独立高斯随机过程〈ξ〉，布郎粒子的位置增量是H（0＜H＜1，称为赫斯特指数）的函数，对寻常布朗运动H=1/2，当它不等于1/2时，这时的布朗运动就叫做分形布朗运动。
#21627. 康托尔集（Cantor set）- 在0＜D H＜1范围内有分形维的分形集称为康托尔集。下图是一个例子，它的分维数是ln2/ln3。
#21628. 自仿射（self-affine）- 由不同因子标度时间和距离的变换称为仿射变换。在一个仿射变换下，重现曲线，叫做自仿射。
#21629. KdV方程（KdV equation）-
考特维克·德佛里于1895年导出了弱非线性浅表水波的运动方程：
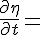
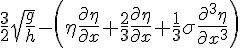
式中η是浅表水波幅度，h乃水道深度，g为重力加速度，σ=h 3/3-Th/gρ，ρ是水的密度，T为表面张力。经变量代换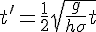
、
、
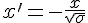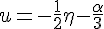(α=1)后，上述方程变为：
u t-6uu x+u xxx=0
这就是KdV方程。
#21630. 孤立子（soliton）- 孤立波发现于1844年，当在运河中的船舶突然停驶时，其两舷的水流会在船首堆起，继续向前，而其形状和幅度均保持不变，这种波称为孤立波。孤立波一般定义为KdV方程的sech平方解。孤立子是孤立波的一种叫法，它不是一个精确的定义，但可以用来描述非线性方程的解：1)表示形状恒定的波；2)在无限远处，其增长或衰减不变；3)与其他孤立子交会之后保持原有形状。
#21631. 缪拉变换（Miula transformation）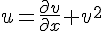
称为缪拉变换，式中v是KdV方程的解，而u则是一种变形KdV（mKdV）方程的解。若令
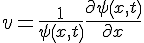
再将u(x,t)用u(x,t)-λ代替（λ为常数），则缪拉变换式就变成一维定常薛定谔方程：
#21632. 散射参量（scattering parameter）- 对一已知的势函数，所有束缚态本征值λ n、归一化常数c n（幅度的测度）以及连续函数a(k)（透射系数）和b(k)（反射系数）的集合称为散射参量。
#21633. 逆散射变换（inverse scattering transformation）-
对定常薛定谔方程，势函数u(x,t)满足KdV方程，且
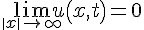。求得全部散射参量
，
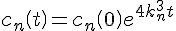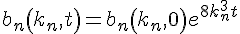，a
n(k
n,t)=a
n(k
n,0)，对ψ(x,t)的时间演化方程，用条件dλ/dt=0，解盖尔芬德-莱维坦-马尔琴柯积分方程：
K(x,y,t)+B(x+y,t)+∫ -∞∞B(y+z,t)K(x,z,t)dz=0
（式中定义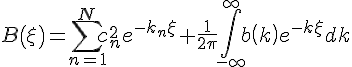
）。若K(x,y)可解得，则势函数为：
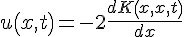
上述过程就叫做逆散射变换。
#21634. 正弦戈尔登方程（sine-Gordon equation）-
正弦戈尔登方程
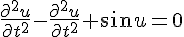是一种重要的非线性方程，它经常出现在微分几何与相对论场论中。它的行波解是u(x,t)=u(x-vt)=f(z)=±4arctan[
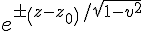]。该解对变量x的一次导数会得到孤立子形状。e指数取正号叫扭结解；取负号叫反扭结解。纽结和反纽结表示了孤立子碰撞的全部性质：孤立子发生碰撞后不受损失而仅有相移。
- #21635. 非线性薛定谔方程（nonlinear Schrödinger equation）
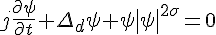是d维σ阶非线性薛定谔方程，其中Δ
d乃d维拉普拉斯算符，
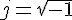。对每个d都能找到一个在有限时间内爆发（或自聚焦奇异性）的σ。所谓“自聚焦”，乃指在适当的初始条件下，当能量小于零时会导致惯量矩在有限时间内消失（在守恒律意义上），结果形成坍缩（爆发）。
#21636. 贝克隆变换（Bäcklund transformation）-
令u(x,t)是偏微分方程D
1(u)=0的解；v(x,t)是偏微分方程D
2(v)=0的解。偏微分关系
B i(u,v)=0 (i=1,2,…,n)
称为贝克隆变换。
-
令覆盖奇异集的非空盒（即小立方块）的总数为N(δ)，而N
i(δ)是第i种盒子的数目，因而这种盒子的概率就是P
i(δ)=N
i(δ)/N(δ)。取对数测度
-
切于中心本征空间的不断流形W
C(0)叫中心流形。一般求法如下：设系统可分为稳定部分
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
