深度学习之残差网络ResNet

写在前面

在深度学习的发展历程中，卷积神经网络的设计深度是一个需要精心权衡的关键参数，网络的深度在本质上起到的主要作用有以下两个大方面。

特征抽象层次

# 不同深度的特征抽象示例
shallow = nn.Sequential(
    nn.Conv2d(3, 64, 3),  # 边缘/纹理特征
    nn.ReLU()
)

deep = nn.Sequential(
    nn.Conv2d(3, 64, 3),
    nn.ReLU(),
    # ... 更多中间层
    nn.Conv2d(512, 1024, 3)  # 语义/物体部件特征
)

• 浅层(1-5层)：捕捉局部边缘、纹理等低级视觉特征
• 中层(5-20层)：识别图案、部件等中级特征组合
• 深层(20+层)：理解语义、物体等高级抽象概念

感受野计算

感受野公式：

RF_l = RF_{l-1} + (k_l - 1) * ∏_{i=1}^{l-1} s_i

其中：

• RF_l：第l层的感受野
• k_l：第l层卷积核尺寸
• s_i：第i层步长
  总结来说，网络的深度是为了最大化的提取目标的特征。

1. 网络深度：双刃剑效应

1.1 深度带来的优势

按道理，网络越深越好，这是正常的逻辑。

• 层次化特征学习：深层网络能够构建从低层边缘特征到高层语义特征的完整层次结构
• 感受野指数增长：通过堆叠卷积层，网络能够捕捉更大范围的上下文信息
• 参数效率提升：小卷积核的堆叠可等效大卷积核效果，但参数量更少

# 传统CNN的层次特征提取示例
class TraditionalCNN(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(3, 64, 3, stride=2)  # 边缘特征
        self.conv2 = nn.Conv2d(64, 128, 3)  # 纹理特征
        self.conv3 = nn.Conv2d(128, 256, 3)  # 部件特征
        self.conv4 = nn.Conv2d(256, 512, 3)  # 语义特征

1.2 深度引发的挑战

但是，在ResNet出现之前，深度卷积神经网络面临两大核心问题：

1. 梯度消失问题
   反向传播时梯度需要跨多层传递，当网络深度超过20层时，梯度值会指数级衰减，导致浅层参数无法有效更新

2. 网络退化问题
   实验表明，56层网络的训练误差和测试误差都比20层网络更高，这不是过拟合导致，而是单纯因为网络难以优化。

问题类型	现象	根本原因
梯度消失	浅层参数更新微弱	反向传播时梯度连乘导致指数衰减
网络退化	增加深度反而降低准确率	优化困难，并非过拟合
计算成本	训练/推理速度下降	层数增加带来的计算量增长

2. 核心问题深度解析

2.1 梯度消失问题

数学原理：

∂L/∂W_l = ∂L/∂y * ∏_{i=l}^{L-1} (W_i^T * σ'(z_i))

其中：

1. ∂L/∂y 是损失函数对网络输出的梯度
2. ∏表示从第l层到输出层L-1层的连乘
3. W_i^T 是第i层权重的转置矩阵
4. σ’(z_i) 是第i层激活函数的导数

这个公式揭示了：

1. 梯度是通过链式法则反向传播的
2. 深层网络的梯度是各层权重矩阵和激活函数导数的连乘积
3. 当层数很深时(L很大)，如果|W_i^T * σ’(z_i)| < 1，连乘结果会指数级减小→梯度消失
4. 如果|W_i^T * σ’(z_i)| > 1，连乘结果会指数级增大→梯度爆炸

2.2 网络退化现象

有很多实验数据表明：

• 56层网络在CIFAR-10上的训练误差和测试误差均高于20层网络
• 这不是过拟合问题（训练误差也更高）
• 深层网络难以学习到恒等映射
  因此，不能盲目的增加网络深度，这往往带来的并不是好处而是坏处。那么有没有什么办法在网络结构设计上去解决这两个大问题呢？答案是有的，那就是残差网络，当然还有其他的方法，在这里，我们只将残差。

3. 残差连接的核心思想

残差连接的核心优势
(1) 解决梯度消失问题

• 传统网络：反向传播时梯度连续相乘导致指数级衰减。
• 残差网络：通过 out += identity 的加法操作，梯度可以直接回传。
  (2) 特征复用机制
• 原始特征通过shortcut直接传递到深层。
• 网络只需学习"残差"（新特征与原始特征的差值）。

3.1 基本结构

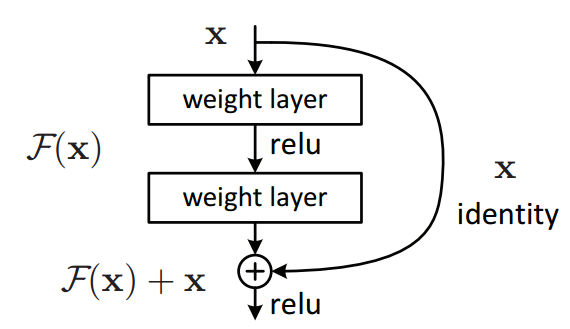
残差块通过引入"跳跃连接"(Skip Connection)，让网络可以学习输入与输出之间的残差：

H(x) = F(x) + x

其中：

• x：输入特征
• F(x)：卷积层学习到的残差
• H(x)：最终输出

3.2 数学原理

假设最优映射为H(x)，传统网络直接学习H(x)，而残差网络学习：

F(x) = H(x) - x

求导结果：
∂H/∂x = ∂F/∂x + 1
即使∂F/∂x很小，梯度也不会消失。

最后，给出一个完整的RestNet18网络结构

import torch
import torch.nn as nn
import torch.nn.functional as F

class BasicBlock(nn.Module):
    expansion = 1
    
    def __init__(self, in_channels, out_channels, stride=1):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=stride, padding=1, bias=False)
        self.bn1 = nn.BatchNorm2d(out_channels)
        self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1, bias=False)
        self.bn2 = nn.BatchNorm2d(out_channels)
        
        self.shortcut = nn.Sequential()
        if stride != 1 or in_channels != out_channels * self.expansion:
            self.shortcut = nn.Sequential(
                nn.Conv2d(in_channels, out_channels*self.expansion, kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(out_channels*self.expansion)
            )

    def forward(self, x):
        identity = x
        out = F.relu(self.bn1(self.conv1(x)))
        out = self.bn2(self.conv2(out))
        out += self.shortcut(identity)
        return F.relu(out)

class ResNet18(nn.Module):
    def __init__(self, num_classes=1000):
        super().__init__()
        self.in_channels = 64
        
        # 初始卷积层
        self.conv1 = nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3, bias=False)
        self.bn1 = nn.BatchNorm2d(64)
        self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
        
        # 4个阶段（共8个BasicBlock）
        self.layer1 = self._make_layer(64, 64, 2, stride=1)    # Stage1: 2个BasicBlock
        self.layer2 = self._make_layer(64, 128, 2, stride=2)    # Stage2: 2个BasicBlock
        self.layer3 = self._make_layer(128, 256, 2, stride=2)   # Stage3: 2个BasicBlock
        self.layer4 = self._make_layer(256, 512, 2, stride=2)   # Stage4: 2个BasicBlock
        
        # 分类头
        self.avgpool = nn.AdaptiveAvgPool2d((1,1))
        self.fc = nn.Linear(512, num_classes)

    def _make_layer(self, in_channels, out_channels, blocks, stride):
        layers = []
        # 第一个Block处理下采样
        layers.append(BasicBlock(in_channels, out_channels, stride))
        # 后续Block保持通道数不变
        for _ in range(1, blocks):
            layers.append(BasicBlock(out_channels, out_channels))
        return nn.Sequential(*layers)

    def forward(self, x):
        # [输入尺寸计算流程]
        x = F.relu(self.bn1(self.conv1(x)))  # [1,3,224,224] → [1,64,112,112]
        x = self.maxpool(x)                   # [1,64,112,112] → [1,64,56,56]
        
        x = self.layer1(x)  # [1,64,56,56] → [1,64,56,56]
        x = self.layer2(x)  # [1,64,56,56] → [1,128,28,28]
        x = self.layer3(x)  # [1,128,28,28] → [1,256,14,14]
        x = self.layer4(x)  # [1,256,14,14] → [1,512,7,7]
        
        x = self.avgpool(x) # [1,512,7,7] → [1,512,1,1]
        x = torch.flatten(x, 1)
        x = self.fc(x)      # [1,512] → [1,num_classes]
        return x

4. 总结

残差连接通过简单的加法操作解决了深度神经网络的核心训练难题，其主要优势：

1. 解决了梯度消失问题
2. 缓解了网络退化现象
3. 实现了特征复用机制
4. 大幅提升了网络深度上限

这种"大道至简"的设计思想也影响了后续Transformer等架构的发展，成为深度学习发展史上的里程碑式创新。