【蓝桥杯】逆波兰表达式

最新推荐文章于 2022-05-03 08:50:52 发布

转载最新推荐文章于 2022-05-03 08:50:52 发布 · 416 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/Aikoin/p/10492392.html

文章标签：

#数据结构与算法

本文介绍了一种用于逆波兰表达式（前缀表达式）解析与计算的递归算法实现。通过分析代码逻辑，文章详细解释了如何将逆波兰表达式转换为数值结果，重点在于递归调用与运算符处理。

逆波兰表达式

正常的表达式称为中缀表达式，运算符在中间，主要是给人阅读的，机器求解并不方便。

例如：3 + 5 * (2 + 6) - 1

而且，常常需要用括号来改变运算次序。

相反，如果使用逆波兰表达式（前缀表达式）表示，上面的算式则表示为：

- + 3 * 5 + 2 6 1

不再需要括号，机器可以用递归的方法很方便地求解。

为了简便，我们假设：

1. 只有 + - * 三种运算符
2. 每个运算数都是一个小于10的非负整数

下面的程序对一个逆波兰表示串进行求值。
其返回值为一个结构：其中第一元素表示求值结果，第二个元素表示它已解析的字符数。

 1 struct EV
 2  {
 3  int result;  //计算结果
 4  int n;       //消耗掉的字符数
 5  };
 6 
 7  struct EV evaluate(char* x)
 8  {
 9  struct EV ev = {0,0};
10  struct EV v1;
11  struct EV v2;
12 
13  if(*x==0) return ev;
14 
15  if(x[0]>='0' && x[0]<='9'){  //字符转数字'1'-'0'=1
16  ev.result = x[0]-'0';
17  ev.n = 1;
18  return ev;   
19  }
20 
21  v1 = evaluate(x+1);
22  v2 = _____________________________;  //填空位置
23 
24  if(x[0]=='+') ev.result = v1.result + v2.result;
25  if(x[0]=='*') ev.result = v1.result * v2.result;
26  if(x[0]=='-') ev.result = v1.result - v2.result;
27  ev.n = 1+v1.n+v2.n;
28 
29  return ev;
30  }

请分析代码逻辑，并推测划线处的代码，通过网页提交。
注意：仅把缺少的代码作为答案，千万不要填写多余的代码、符号或说明文字！！

今天刚好数据结构课上讲到了前缀表达式，其实就是从第一个字符开始看，如果是运算操作符而后面刚好跟着两个表达式（比如+AB），那么就是这两个表达式进行该运算（+AB即为A+B）。

观察代码，也是从第一个字符开始：如果是数字，那么直接返回；如果不是，说明遇到了一个操作符，那么v1从这个操作符的后一位字符开始递归，直到遇到数字返回；然后v2再进行一些操作；最后把v1和v2对应的值对于回溯时最近的那个操作符进行运算。那么很显然，v2是从v1结束递归后的后一个偏移量开始递归，也就是v1开始递归前的位置往后数n个（结束时v1的偏移量）。即：

v1 = evaluate(x + 1);
v2 = evaluate(x + 1 + v1.n);  //填空位置

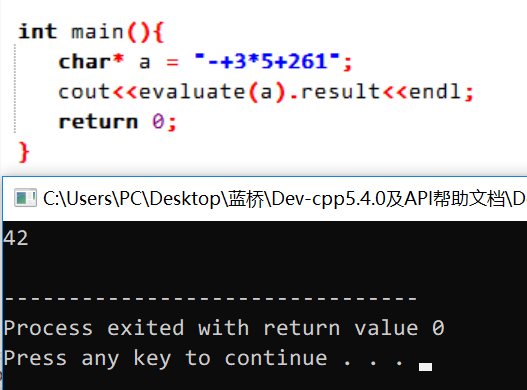
最后再手动加上main函数验证一下~嗯，42，对了~

转载于:https://www.cnblogs.com/Aikoin/p/10492392.html