【蓝桥杯】振兴中华

振兴中华

小明参加了学校的趣味运动会，其中的一个项目是：跳格子。

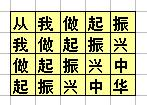
地上画着一些格子，每个格子里写一个字，如下所示：

从我做起振
我做起振兴
做起振兴中               
起振兴中华

比赛时，先站在左上角的写着“从”字的格子里，可以横向或纵向跳到相邻的格子里，但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。

要求跳过的路线刚好构成“从我做起振兴中华”这句话。

请你帮助小明算一算他一共有多少种可能的跳跃路线呢？

 

这道题要我们枚举所有的可能，枚举有两种方法：递归和迭代。

这道题用递归做较简单，递归有三个要素：

找重复，利用重复不断减小问题的规模；

找变化，变化的状态量就是递归的参数；

找出口，判断什么可以退出递归。

观察题目，其实在每个格子上时都只能向下走或者向右走，在当前格子上有两种走法；而当到达边界处时，比如走到最下面一行格子或者最右边一列格子时，只能一路向右走，这时从当前格子走到最后只能有一种走法。

 1 #include <iostream>
 2 using namespace std;
 3 
 4 int f(int x,int y){   //变化的状态量就是当前的坐标（找变化）
 5     if(x==3||y==4) return 1;  //如果走到边界，只有一种走法，直接return 1（找出口）
 6     return f(x+1,y)+f(x,y+1); //没有走到边界，那么当前格子有两种走法，两者相加就是从当前格子走到最后的方法数 （找重复）
 7 }
 8 
 9 int main()
10 {
11     cout<<f(0,0)<<endl;
12     return 0;
13 }

运行结果：

 

转载于:https://www.cnblogs.com/Aikoin/p/10471509.html