快速排序

快速排序(Quick Sort)是对冒泡排序的一种改进，基本思想是选取一个数作为关键字，经过一趟排序，将整段序列分为两个部分，其中一部分的值都小于关键字，另一部分都大关键字。然后继续对这两部分继续进行排序，从而使整个序列达到有序。
递归实现：

void QuickSort(int* arr, int left, int right)
{
	int mid = 0;
	if(left >= right)//表示完成一组的排序
		return;
	mid = PartSort1(arr, left, right);关键字的位置
	QuickSort(arr, left, mid-1);
	QuickSort(arr, mid+1, right);
}

PartSort()函数是进行一次快排的算法。
对于PartSort的函数有很多，这里展示三种。

左右指针法

1、选取一个关键字(key)，一般取整组记录的第一个数/最后一个，这里采用选取数组的第一个数为key。
2、设置两个变量left = 0;right = N - 1;
3、从left一直向后走，直到找到一个大于key的值，right从后至前，直至找到一个小于key的值，然后交换这两个数。
4、重复第三步，一直往后找，直到left和right相遇，这时将key放置left的位置即可。

根据上面的思想，可以写出下面的代码

int PartSort1(int* arr, int left, int right)
{
	int key;
	int start = left;
	key = arr[left];
	while(left < right)
	{
		while(left < right && arr[right] >= key)
		{
			right--;
		}
		while(left < right && arr[left] <= key)
		{
			left++;
		}
		
		Swap(&arr[left], &arr[right]);
	}
	Swap(&arr[left], &arr[start]);
	return left;
}

挖坑法

1、选取一个关键字key，一般取整组记录的第一个数/最后一个，这里采用选取数组第一个元素key，也是初始的坑位。
2、设置两个变量left = 0;right = N - 1;
3、right一直向前走，直到找到一个小于key的值，然后将该数放入坑中，坑位变成了arr[right]。
4、left一直向前走，直到找到一个小于key的值，然后将该数放入坑中，坑位变成了arr[left]。
5、重复3和4的步骤，直到left和right相遇，然后将key放入最后一个坑位。

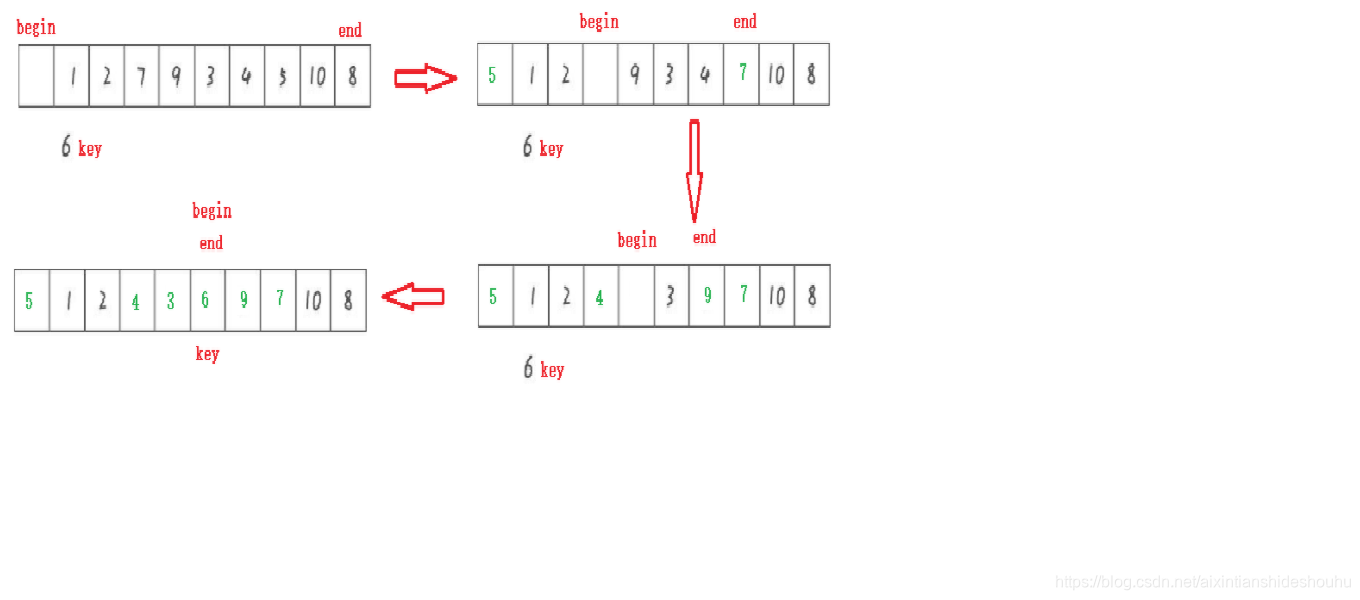
代码如下

int PartSort2(int* arr, int left, int right)
{
	int key = arr[left];
	while(left < right)
	{
		while(left < right && arr[left] >= key)
		{
			right--;
		}
		arr[left] = arr[right];
		while(left < right && arr[left] <= key)
		{
			left++;
		}
		arr[right] = arr[left];	
	}
	arr[left] = key;
	return left;
}

前后指针法

1、定义变量prev指向序列的开头，定义变量cur指向prev的后一个位置。
2、当arr[cur] < key时，cur和prev同时往后走，如果arr[cur]>key，cur往后走，pre留在大于key的数值前一个位置。
3、当arr[cur]再次 < key时，交换array[cur]和array[pre]。
简单来说就是，在没找到大于key值前，pre永远紧跟cur，遇到大的两者之间机会拉开差距，中间差的肯定是连续的大于key的值，当再次遇到小于key的值时，交换两个下标对应的值就好了

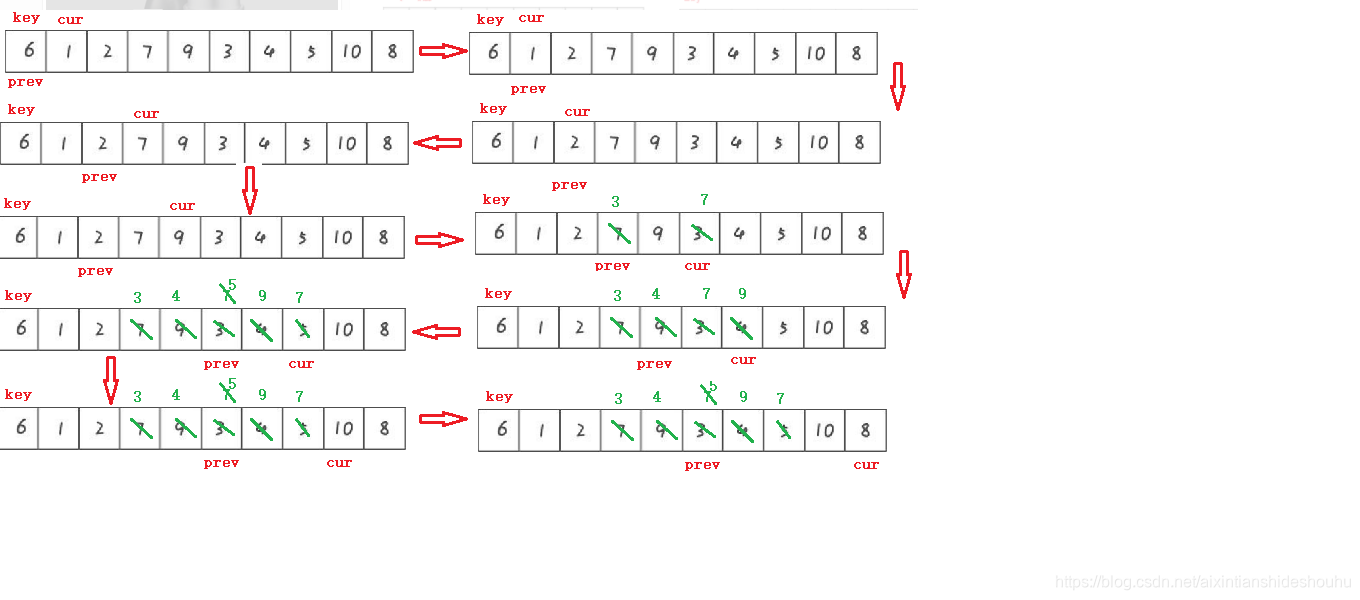
代码如下

int PartSort3(int* arr, int left, int right)
{
	int key = arr[left];
	int prev = left;
	int cur = left+1;
	while(cur <= right)
	{
		if(arr[cur] < key && (++prev) != cur)
		{
			Swap(&arr[prev], &arr[cur]);
		}
		++cur;
	}
	Swap(&arr[left], &arr[prev]);
	return prev;
}

快排的优化
首先快排的思想是找一个关键字，然后以关键字为中介线，一遍都小于它，另一边都大于它，然后对两段区间继续划分，那么关键字的选取就很关键。
1、三数取中法
上面的代码思想都是直接拿序列的第一个值作为关键字，如果最后这个值刚好是整段序列最大或者最小的值，那么这次划分就是没意义的。
所以当序列是正序或者逆序时，每次选到的关键字都是没有起到划分的作用。快排的效率会退化。
所以可以每次在选枢轴时，在序列的第一，中间，最后三个值里面选一个中间值出来作为枢轴，保证每次划分接近均等
2、小区间优化
由于是递归程序，每一次递归都要开辟栈帧，当递归到序列里的值不是很多时，我们可以采用直接插入排序来完成，从而避免这些栈帧的消耗。

整个代码如下：

//三数取中
int GetMid(int* arr, int left, int right)
{
	int mid = left + ((right-left)>>1);
	if(arr[left] <= arr[right])
	{
		if(arr[mid] < arr[left])
		{
			return left;
		}
		else if(arr[mid] > arr[right])
		{
			return right;
		}
		else
		{
			return mid;
		}
	}
	else
	{
		if(arr[mid] < arr[right])
		{
			return right;
		}
		else if(arr[mid] > arr[left])
		{
			return left;
		}
		else
		{
			return mid;
		}
	}

}
//左右指针法
int PartSort1(int* arr, int left, int right)
{
	
	int key;
	int start = left;
	int mid = GetMid(arr, left, right);
	Swap(&arr[mid], &arr[left]);
	key = arr[left];
	while(left < right)
	{
		while(left < right && arr[right] >= key)
		{
			right--;
		}
		while(left < right && arr[left] <= key)
		{
			left++;
		}
		Swap(&arr[left], &arr[right]);
	}
	Swap(&arr[left], &arr[start]);
	return left;
}

//挖坑法
int PartSort2(int* arr, int left, int right)
{
	int mid = GetMid(arr, left, right);
	Swap(&arr[left], &arr[mid]);
	int key = arr[left];
	
	while(left < right)
	{
		while(left < right && arr[left] >= key)
		{
			right--;
		}
		arr[left] = arr[right];
		while(left < right && arr[left] <= key)
		{
			left++;
		}
		arr[right] = arr[left];	
	}

	arr[left] = key;
	return left;
}

//前后指针法
int PartSort3(int* arr, int left, int right)
{
	int mid = GetMid(arr, left, right);
	Swap(&arr[left], &arr[mid]);
	int key = arr[left];
	int prev = left;
	int cur = left+1;
	while(cur <= right)
	{
		if(arr[cur] < key && (++prev) != cur)
		{
			Swap(&arr[prev], &arr[cur]);
		}
		++cur;
	}
	Swap(&arr[left], &arr[prev]);
	return prev;
}
void QuickSort(int* arr, int left, int right)
{
	int mid = 0;
	if(left >= right)
		return;
	//小区间优化
	if((right - left) <= 5)
	{
		InsertSort(arr, right-left+1);
	}
	mid = PartSort3(arr, left, right);
	QuickSort(arr, left, mid-1);
	QuickSort(arr, mid+1, right);
}

非递归实现
递归的算法主要是在划分子区间，如果要非递归实现快排，只要使用一个栈来保存区间就可以了。
一般将递归程序改成非递归首先想到的就是使用栈，因为递归本身就是一个压栈的过程。

void QuickSortNoR(int* arr, int left, int right)
{
	
	int mid = 0;
	int begin,end;
	Stack s;
	StackInit(&s, 3);
	StackPush(&s, right);
	StackPush(&s,left);
	while(StackEmpty(&s) != 0)
	{
		begin = StackTop(&s);//取出左边区间
		StackPop(&s);
		end = StackTop(&s);//起初右边区间
		StackPop(&s);
		mid = PartSort1(arr, begin, end);
		if((mid+1) < right)
		{
			StackPush(&s, right);
			StackPush(&s,mid+1);
		}
		if((mid-1) > left)
		{
			StackPush(&s, mid-1);
			StackPush(&s, left);
		}
	}
}