Top-K问题(N个数，找前K个最大的或者前K个最小的，利用堆）-优快云博客

本文链接：https://blog.youkuaiyun.com/aitexuexue/article/details/127836186

在大数据量场景下，解决Top-K问题不宜直接排序。可以使用堆来高效地找到前K个最大或最小的元素。通过建立小堆（升序）或大堆（降序），遍历数据集并与堆顶元素比较，根据比较结果更新堆，最终得到所需结果。这种方法空间复杂度为O(K)，时间复杂度为K+LogK*(N-K)。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Top-K问题

即求取数据结合中前K个最大的元素或者最小的元素，一般情况下数据量比较大。
想到的第一个方法就是排序，但是如果数据量非常大，排序就不太适合（数据可能都不能一下子全部加载到内存中）。
所以我们可以利用堆来解决。
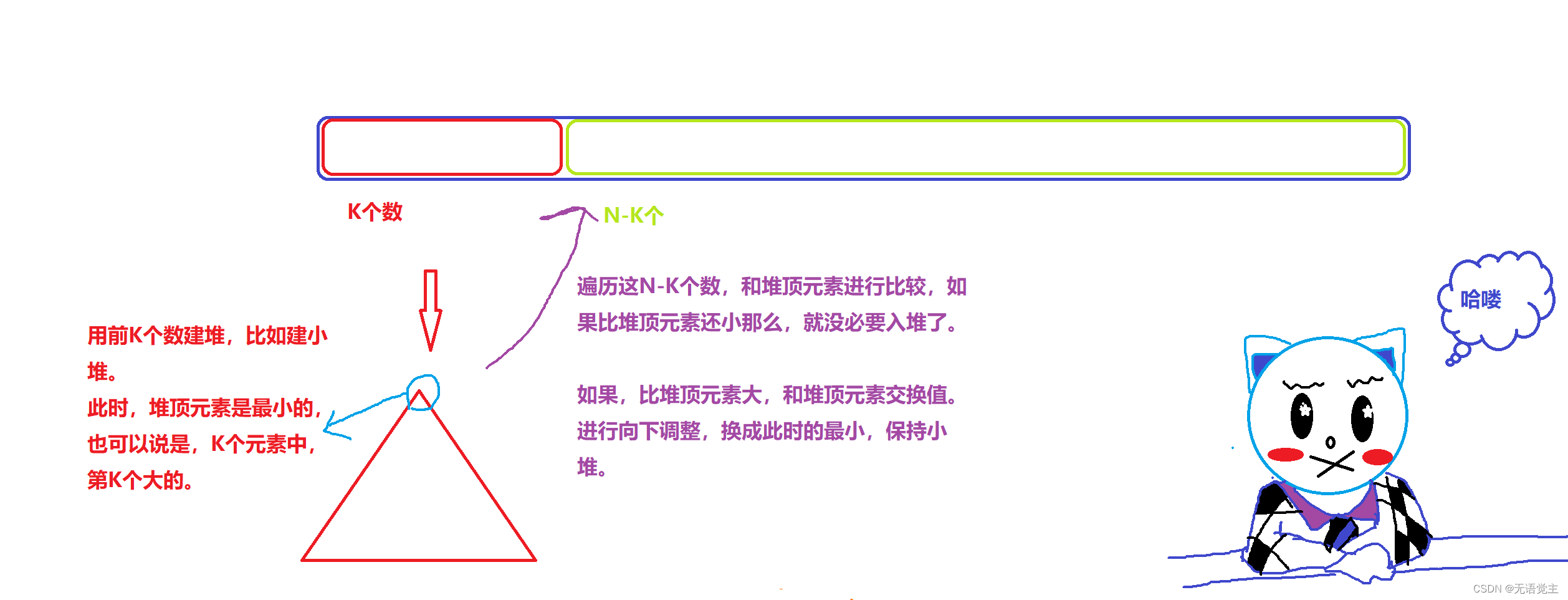
在这里插入图片描述

假设有N个数据，要选取前K个大或者，前K个小

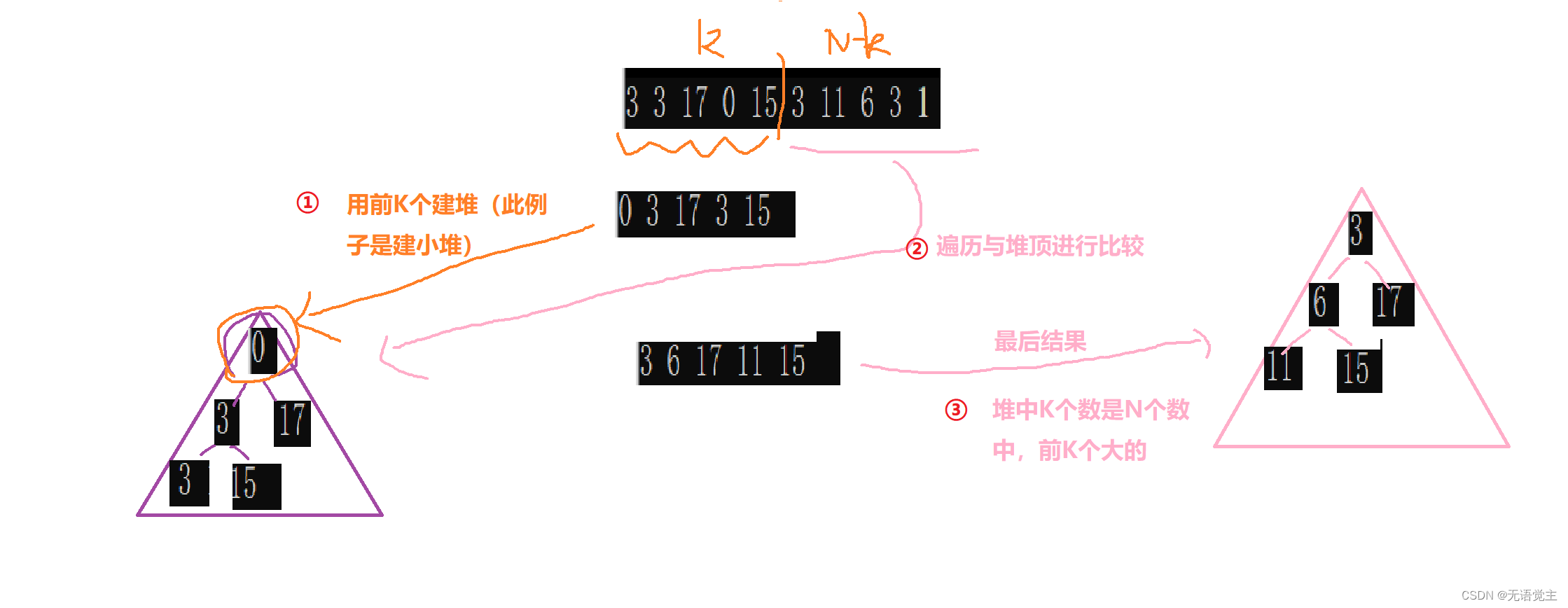
取数据集合前K个数建小堆或者大堆。用一个数组存放。

排升序---->建小堆（此时堆顶是第K大的数，就是这K个数最小的
排降序---->建大堆（此时堆顶是第K小的数，就是这前K个最大的

依次遍历剩余的N-K个数与堆顶进行比较，
①升序，小堆，如果数比堆顶小，不用入堆，比最小的都小，也不可能比堆里其他的大了；那下一个数进行比较，当那个数比它大，OK，替换堆顶，它入堆，进行向下调整建小堆。
②降序，大堆，如果数比堆顶大，不用入堆，比最大的都大，也不可能比堆里其他的小了；就下一个数进行比较，当那个数比他小，ok \ ( ^ o ^ ) /~,替换堆顶，进行向下调整建大堆。

举个栗子：在这里插入图片描述

在这里插入图片描述空间复杂度：O(K)。只用了额外的K个空间。
时间复杂度：K+(LogK)*(N-K)==>
遍历K次建的堆，向下调整最坏向下调整次数

//TOP--K问题
//
void PrintTopK(int* a, int n, int k)
{
   
   
	//1.用a的前K个数据建堆
	//K个数据，最后一个下标K-1，
	//从最后一个叶子的父节点开始向下调整建
	//建K个数的小堆，这是前K个大的，堆顶是最小的
	//没有按照升序排，只是，选出前K个大的
	for (int i = (k -