反向传播算法：误差的逆向旅行

最新推荐文章于 2025-12-05 14:37:41 发布

原创

最新推荐文章于 2025-12-05 14:37:41 发布 · 672 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#算法

过去十年，深度学习从一个学术概念变成了工业界的标配工具。但很多开发者在使用 TensorFlow 或 PyTorch 训练模型时，只知道调用 loss.backward()，却不知道误差信号是如何从输出层一层层倒流回输入层的。当网络不收敛、梯度消失、训练卡住时，只能盲目调参，却无法定位问题根源。

反向传播算法，就是让神经网络"学会"的核心机制。它不是自动求导库的魔法，而是链式法则在计算图上的工程实现。理解它，你就能看懂为什么某些网络结构会失败，为什么某些激活函数更适合深层网络，为什么残差连接能让训练更稳定。

（示意图占位：《backpropagation neural network diagram》 — 可谷歌搜索："backpropagation diagram"）

为什么需要反向传播？

想象你在教一个机器人识别猫和狗。你给它看一张图片，它给出预测，如果错了，你需要告诉它"哪里错了，错多少"。但问题是，这个机器人有成千上万个"神经元"（权重参数），你不可能手动告诉每个神经元该调整多少。

反向传播就是解决这个问题的：它把"最终预测错了多少"这个单一信号，自动分解到每个权重上，告诉每个参数"你对最终误差贡献了多少，应该往哪个方向调整"。这就像在一个复杂的工厂里，当最终产品不合格时，反向追踪每个环节的责任，让每个工位都知道自己该改进什么。

链式法则：误差传播的数学桥梁

反向传播的核心是链式法则。假设你有一个三层网络：输入层、隐藏层、输出层。损失函数是 $L$ ，你想知道第一层权重 $W_1$ 对损失的影响。

链式法则告诉我们：
$∂L∂W1=∂L∂a3⋅∂a3∂a2⋅∂a2∂a1⋅∂a1∂W1\frac{\partial L}{\partial W_1} = \frac{\partial L}{\partial a_3} \cdot \frac{\partial a_3}{\partial a_2} \cdot \frac{\partial a_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial W_1}$

这个公式的意思是：最终误差对第一层权重的影响，等于"误差对输出的影响"乘以"输出对隐藏层的影响"乘以"隐藏层对输入层的影响"乘以"输入层对权重的影响"。每一层的梯度，都是后面所有层梯度的累积乘积。

这就是为什么深层网络容易出现梯度消失：如果每一层的梯度都小于 1（比如 sigmoid 在饱和区的梯度是 0.25），经过 10 层后，梯度就变成了 $0.2510≈0.0000010.25^{10} \approx 0.000001$ ，几乎为零。第一层的权重几乎不会更新，网络就"学不动"了。

（示意图占位：《chain rule backpropagation flowchart》 — 可谷歌搜索：“chain rule backpropagation flowchart”）

（meme 占位：“gradient vanishing meme funny” 搜索推荐图）

前向传播 vs 反向传播：一个完整的训练循环

让我们用一个具体的例子来理解。假设你要训练一个网络学习 XOR 问题（异或运算）：输入 (0,0) 输出 0，输入 (0,1) 输出 1，输入 (1,0) 输出 1，输入 (1,1) 输出 0。

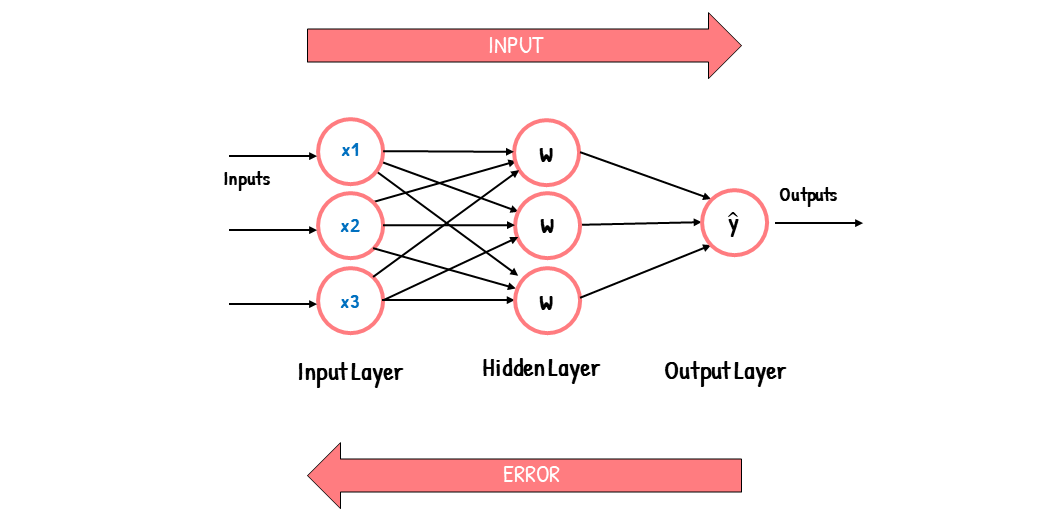
前向传播：数据从输入层流向输出层，每一层做线性变换（加权求和）和非线性变换（激活函数），最终得到预测值。

反向传播：从输出层开始，计算损失函数对输出的梯度，然后一层层往回传，计算每一层的权重梯度，最后用梯度下降更新权重。

这个过程就像：前向传播是"送信"，把原始数据送到最后一层；反向传播是"回执"，把"预测错了多少"这个信息一层层传回来，告诉每一层该调整多少。

动手实现：从零开始写反向传播

理解了原理，我们来实现一个完整的反向传播算法。这个实验会让你看到梯度是如何计算的，权重是如何更新的，网络是如何"学会"的。

环境配置

# 创建虚拟环境
python3 -m venv backprop-env
source backprop-env/bin/activate  # Windows: backprop-env\Scripts\activate

# 安装依赖
pip install numpy matplotlib

核心代码：手动实现反向传播

# file: backprop_from_scratch.py
import numpy as np

class NeuralNetwork:
    def __init__(self, input_size, hidden_size, output_size, learning_rate=0.5