1. 逻辑回归模型为什么可以进行二分类?
- 逻辑回归的表达式为:
y=f(WX+b)y = f(WX + b)y=f(WX+b)
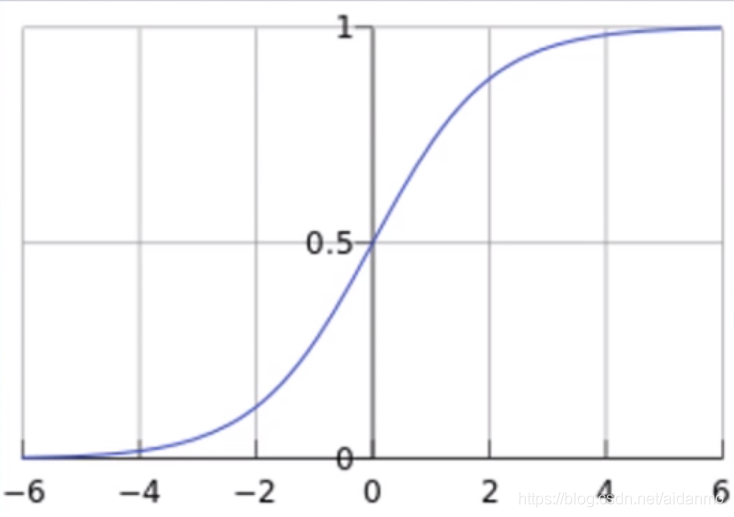
f(x)=11+e−xf(x) = \frac{1}{1 + e^{-x}}f(x)=1+e−x1
该函数的作用是将输入的数据映射到0至1之间,恰恰处于概率取值区间,只需要设置一个阈值,输出y就可以用于解决二分类问题。
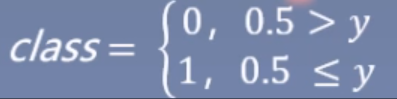
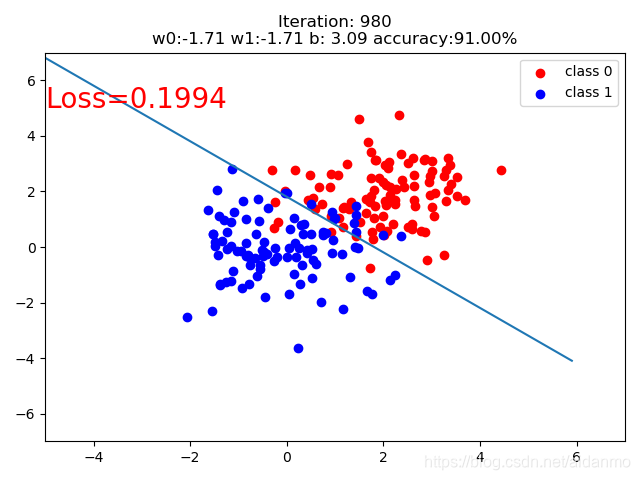
2. 采用代码实现逻辑回归模型的训练,并尝试调整数据生成中的mean_value,将mean_value设置为更小的值,例如1,或者更大的值,例如5,会出现什么情况?再尝试仅调整bias,将bias调为更大或者负数,模型训练过程是怎么样的?
当mean_value=1时,正负样本数据较差较多,采用二分类的逻辑回归模型无法达到很高(99%)的准确度。
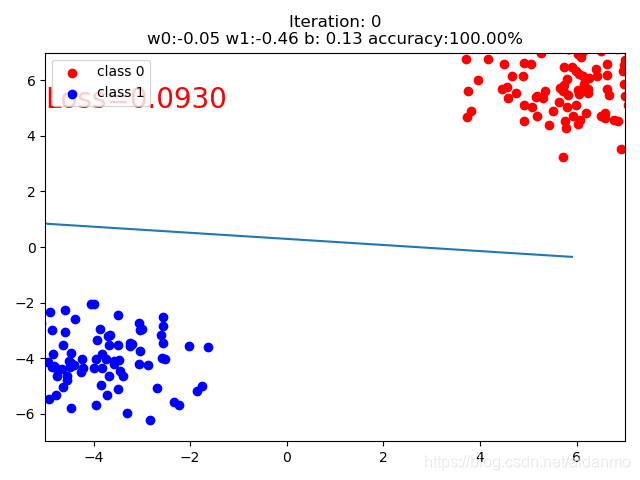
当mean_value=5时,正负样本有非常明显的边界,逻辑回归模型很容易就能将两类样本分开。
调整bias的大小,数据的整体位置会发生偏移。
bias=-10
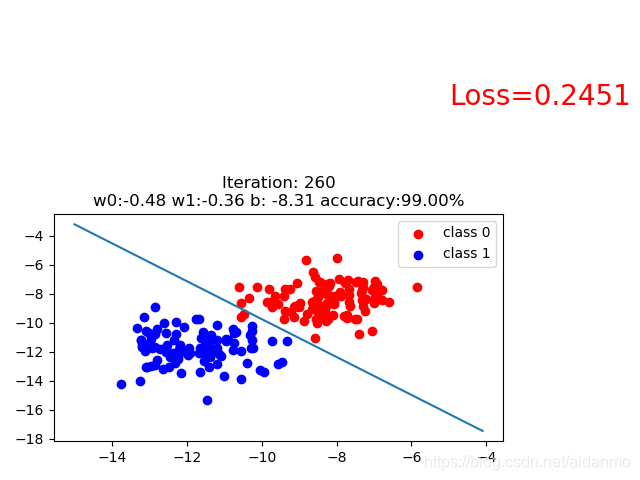
bias=5
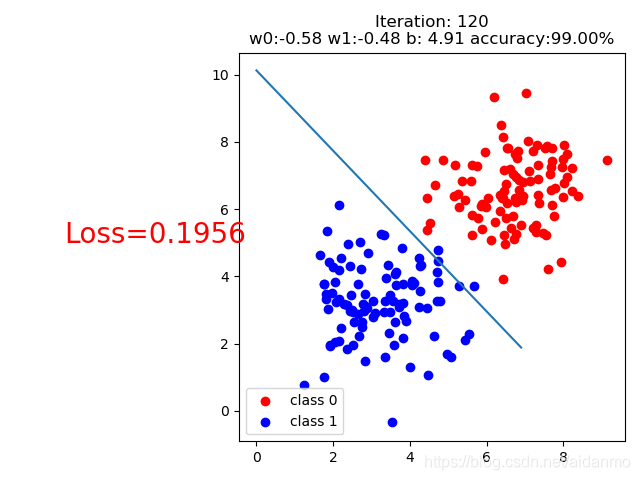
但是当我们继续增加bias的大小时,会发现,无论我们训练多少次,模型也无法将正负样本分开,这是因为随着bias的增大,sigmoid函数在进行反向传播时,梯度接近于0,这时无论迭代多少次,参数都不会更新,这也是为什么需要将数据进行归一化的原因





 本文探讨了逻辑回归模型如何应用于二分类问题,通过调整数据集的mean_value和bias,观察模型训练的效果变化。揭示了不同数据分布下逻辑回归的表现,以及bias对数据整体位置的影响。
本文探讨了逻辑回归模型如何应用于二分类问题,通过调整数据集的mean_value和bias,观察模型训练的效果变化。揭示了不同数据分布下逻辑回归的表现,以及bias对数据整体位置的影响。

















 138
138

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










