Lc2045到达目的地的第二短时间

2045. 到达目的地的第二短时间

help
城市用一个 双向连通 图表示，图中有 n 个节点，从 1 到 n 编号（包含 1 和 n）。图中的边用一个二维整数数组 edges 表示，其中每个 edges[i] = [ui, vi] 表示一条节点 ui 和节点 vi 之间的双向连通边。每组节点对由 最多一条 边连通，顶点不存在连接到自身的边。穿过任意一条边的时间是 time 分钟。

每个节点都有一个交通信号灯，每 change 分钟改变一次，从绿色变成红色，再由红色变成绿色，循环往复。所有信号灯都 同时 改变。你可以在 任何时候 进入某个节点，但是 只能 在节点 信号灯是绿色时 才能离开。如果信号灯是 绿色 ，你 不能 在节点等待，必须离开。

第二小的值 是 严格大于 最小值的所有值中最小的值。

• 例如，[2, 3, 4] 中第二小的值是 3 ，而 [2, 2, 4] 中第二小的值是 4 。

给你 n、edges、time 和 change ，返回从节点 1 到节点 n 需要的 第二短时间 。

注意：

• 你可以 任意次 穿过任意顶点，包括 1 和 n 。
• 你可以假设在 启程时 ，所有信号灯刚刚变成 绿色 。

示例 1：

     

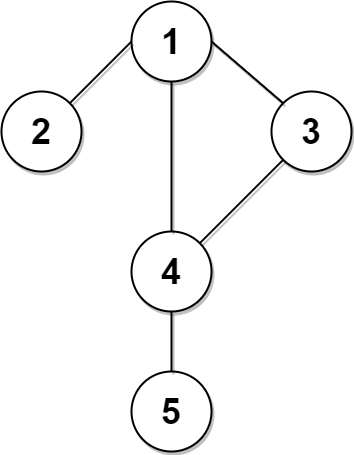
输入：n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
输出：13
解释：
上面的左图展现了给出的城市交通图。
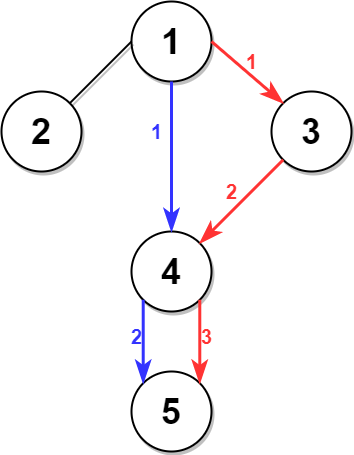
右图中的蓝色路径是最短时间路径。
花费的时间是：
- 从节点 1 开始，总花费时间=0
- 1 -> 4：3 分钟，总花费时间=3
- 4 -> 5：3 分钟，总花费时间=6
因此需要的最小时间是 6 分钟。

右图中的红色路径是第二短时间路径。
- 从节点 1 开始，总花费时间=0
- 1 -> 3：3 分钟，总花费时间=3
- 3 -> 4：3 分钟，总花费时间=6
- 在节点 4 等待 4 分钟，总花费时间=10
- 4 -> 5：3 分钟，总花费时间=13
因此第二短时间是 13 分钟。      

示例 2：

输入：n = 2, edges = [[1,2]], time = 3, change = 2
输出：11
解释：
最短时间路径是 1 -> 2 ，总花费时间 = 3 分钟
最短时间路径是 1 -> 2 -> 1 -> 2 ，总花费时间 = 11 分钟

解决

关键点是

• 严格的次路径
• 如何表示红绿灯的状态(tar_time/change)%2==1就是红灯，其中tar_time代表的是离开当前点的时间,如果是红灯还需要补偿这个等红灯时间
• 如何确保这个点最多访问两次，防止无限循环，就不能用bool marked[]了，而是用来两个unordered_map<node,time>去进行标记，到达每一个节点的最小值和严格次小值

代码

class Solution {
public:
    int secondMinimum(int n, vector<vector<int>>& edges, int time, int change) {
        // 一个点最多能经历两次
        unordered_map<int,int> first; // node time
        unordered_map<int,int> second;
        // 建图
        unordered_map<int,vector<int>> G;
        int first_time = -1; // 确保严格最小
        for(auto& e : edges) {
            G[e[0]].push_back(e[1]);
            G[e[1]].push_back(e[0]);
        }
        queue<pair<int,int>> Q;
        Q.push({1,0});  // node 到达这个节点的当前时间
        while(!Q.empty()) {
            int size = Q.size();
            // cout<<"size: "<<size<<endl;
            for(int i=0;i<size;i++) {
                auto node = Q.front();
                Q.pop();
                int cur_time = node.second; // 当前点的离开时间
                int v = node.first;                
                for(auto& w : G[v]) {
                    // 下一个点是终点
                    if(w == n) {
                        if(first_time==-1) { // 第一次到达
                            first_time = cur_time+time; // 上一个点出来的时间+time
                        } else if(first_time<cur_time+time) {  // 严格的次小，防止相等的情况
                            return cur_time+time;
                        }
                    }

                    int tar_time = cur_time+time; // 到达当前带点的时间

                    if((tar_time/change)%2==1) {  // red红灯
                        // 多等红绿灯
                        tar_time=(tar_time/change+1)*change; // 当前点的离开时间
                    }

                    // cout<<"w: "<<w<<endl;
                    if(first.find(w)==first.end()) {
                        first[w]=tar_time;
                        Q.push({w,tar_time});
                        continue;
                    }

                    if(second.find(w)==second.end() && tar_time>first[w]) {
                        // 严格的次小
                        Q.push({w,tar_time});
                        second[w]=tar_time;
                        continue;
                    }
                }


            }

        }

        return -1;

    }
};