1004. 最大连续1的个数 III

最新推荐文章于 2022-05-07 09:21:01 发布

原创最新推荐文章于 2022-05-07 09:21:01 发布 · 111 阅读

0 ·

CC 4.0 BY-SA版权

leetcode刷题之旅专栏收录该内容

39 篇文章

订阅专栏

本文探讨了如何改进算法，解决一个中等难度的编程问题，即在给定数组A和翻转次数K的情况下，找到最长连续1子数组。原始动态规划方法在K较大时效率低下，通过滑动窗口技巧优化，提升了空间复杂度，使代码在K大时也能快速求解。

1004. 最大连续1的个数 III

难度中等234

给定一个由若干 0 和 1 组成的数组 A，我们最多可以将 K 个值从 0 变成 1 。

返回仅包含 1 的最长（连续）子数组的长度。

示例 1：

输入：A = [1,1,1,0,0,0,1,1,1,1,0], K = 2
输出：6
解释： 
[1,1,1,0,0,1,1,1,1,1,1]
粗体数字从 0 翻转到 1，最长的子数组长度为 6。

示例 2：

输入：A = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3
输出：10
解释：
[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
粗体数字从 0 翻转到 1，最长的子数组长度为 10。

这是个简单时间序列类型的动态规划题目，有权利可以翻转

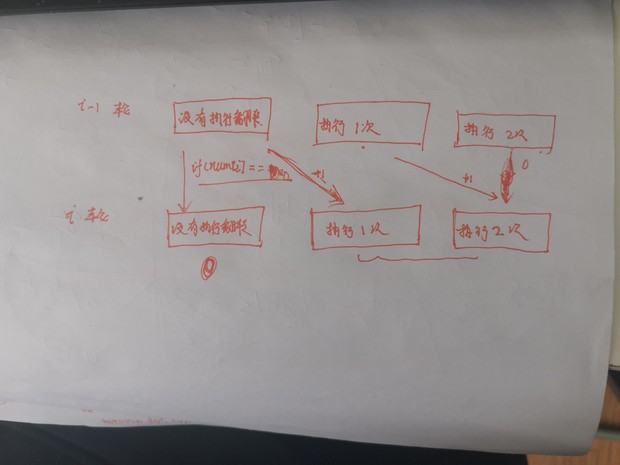
Images

class Solution {
public:
    int longestOnes(vector<int>& A, int K) {
        if(K>=A.size()) {
            return A.size();
        }
        vector<vector<int>> dp(A.size(),vector<int>(K+1,1));
        // BASE CASE
        if(A[0]==0&&K==0) {
            for(int i=0;i<K+1;i++) {
                dp[0][i]=0;
            }
        }
        
        for(int i=1;i<A.size();i++) {
            for(int j=0;j<K+1;j++) {
                if(A[i]==0) {
                    if(j==0) {
                        dp[i][j]=0;
                    } else {
                        dp[i][j]=dp[i-1][j-1]+1;
                    }
                    } else {
                    dp[i][j]=dp[i-1][j]+1;
                    }


        }

    }
    // for(auto a:dp) {
    //     for(auto b:a) {
    //         cout<<b<<" ";
    //     }
    //     cout<<endl;
    // }
    int res=0;
    for(int k=0;k<A.size();k++) {
        res=max(res,dp[k][K]);
    }

    return res;
    }
};

但是k大的时候就不适用，因为k太大dp数组就越大，执行会超时

改用滑动窗口

class Solution {
public:
    int longestOnes(vector<int>& A, int K) {
        //滑动窗口
        int left=0,right=0;
        int nums=0;
        int res=0;
        while(right<A.size()) {
            int input=A[right];
            right++;    //右移动窗口

            if(input==0) {
                nums++;
            }
            // for(int k=left;k<right;k++) {
            //     cout<<A[k];
            // }
            // cout<<endl;

            while(nums>K) {
                    int output=A[left];
                left++;
              res=max(res,right-left);   
                if(output==0) {
                    nums--;
                }
            }
        }

        return max(res,right-left);
    }
};