边缘计算中混合去中心化数据分析

边缘计算赋能的物联网网络中的混合去中心化数据分析

摘要

边缘计算通过将计算和数据分析置于数据生成位置附近，正成为物联网（IoT）网络的一种新型基础设施。本文提出了一种面向边缘计算的新型数据分析框架。该框架基于一种新的去中心化算法，使所有节点无需共享原始数据即可获得全局最优模型。所形成的方案以混合模式执行：本地物联网节点将计算信息发送至边缘节点，边缘节点仅通过与其邻居交换分析结果进行协作。本文对所提出的方法在多种应用中进行了分析与评估，实验结果表明，该方法能有效为边缘计算基础设施提供快速的数据分析能力。

索引术语 —数据分析，去中心化算法，边缘计算，物联网(物联网)。

一、引言

物联网（IoT）有望代表互联网的下一次演进，通过从物联网设备收集的海量数据中提取和积累知识来推动发展[1]。借助云，如今许多物联网应用简单地将所有原始数据传输到云中进行处理和分析。然而，这种方法存在若干局限性。首先，数据量过大。随着物联网的部署和发展，物联网设备产生的数据量不断增加，由于带宽限制[2]，可能无法将所有原始数据通过网络传输到云。其次，延迟较高。对于某些对时间敏感的应用，这种基于云的解决方案因数据在云中移动、处理和分析所造成的延迟而受到限制。第三，隐私受限。在医疗保健等领域，医疗数据无法被传输，因此这种“先收集后处理”的方法不适用于以隐私为中心的应用。

最近，提出了边缘计算基础设施。其理念是将计算和分析功能移至数据生成的位置附近。该架构在解决上述一些问题方面具有前景，例如，通过将计算卸载到边缘节点[3],[4]来降低延迟。此外，一些近期研究聚焦于边缘计算中计算卸载的资源分配与能效问题，并已在[5]和[6]中开展。然而，这些工作仍未解决隐私问题，仍将其作为一个开放性问题遗留下来，因为物联网设备生成的原始数据仍然需要传输至边缘节点。作为一种可能的解决方案，联邦学习（FL）——一种数据分析和机器学习的新范式——可应用于物联网设备，以在不共享其原始数据的情况下联合训练模型[7]。但其局限性在于采用了参数服务器架构，即需要一个中心服务器（如远程云）来聚合来自物联网设备的参数估计，因此容易受到单点故障的影响。也就是说，一旦服务器宕机，数据分析过程将中断。考虑到上述问题，一个自然的问题是：我们能否设计一种能够适应边缘计算基础设施并有效应对上述所有问题的数据分析方案？为回答这一问题，我们提出了一种新的去中心化算法，并将其适配为一种混合协议，用于在边缘计算赋能的物联网网络中实施。在我们的协议中，物联网节点根据邻近关系将其梯度信息传输至对应的边缘节点，随后这些边缘节点通过与其直接邻居交换估计值进行协作，以获得全局最优解。所提出的框架在整个数据分析过程中无需原始数据共享。此外，该框架不依赖中心融合中心，任意节点的故障不会阻碍其他节点继续执行数据分析。

本文的结构如下。第二节讨论相关工作。第三节描述问题建模。第四节提出所设计的去中心化算法及其收敛性。第五节描述基于去中心化算法的混合协议在边缘计算基础设施中的应用。第六节展示了所提出协议在两个应用中的评估结果。最后，第七节给出我们的结论。

II. 相关工作

在分布式计算范式中，每个节点持有私有的目标函数，并仅与其直接邻居协作以交换信息来实现全局目标。根据每个节点在计算和通信中的运行模式，去中心化算法可分为同步或异步。一系列用于求解一般凸优化的同步算法已在[8]–[13]中提出了针对这些问题的方案。然而，每个节点需要等待其最慢邻居的信息才能继续执行。一种基于广播八卦的异步算法首次在[14]中提出，用于解决平均一致性问题。内迪奇在[15]中开发了新的异步算法，采用了类似的随机广播机制，但考虑了具有“真实”目标函数的凸优化问题。文献[15]中算法的计算部分依赖于每个节点本地简单而高效的(次)梯度-based更新。需要注意的是，我们所提出的算法专注于改进每个节点的本地更新规则，以减少与邻居之间所需的通信轮次。这基于分布式/去中心化计算中的一个自然事实：更优化的本地节点更新可以使节点间为实现收敛所需的信息交换减少。具体而言，除了使用梯度下降进行本地更新外，我们的设计还结合了邻居的梯度信息和动量[16]，以加速所有节点达到最优解的整个过程。本文的主要贡献有三个方面。

1) 提出了一种新型的去中心化数据分析算法。
2) 设计了一种混合去中心化协议，以将所提出的算法适配到物联网网络的边缘计算基础设施中。
3) 分析了所提出算法的收敛性，确保所有节点最终都能达到相同的最优解。

III. 问题描述

我们考虑一个无向连通网络 G=(V, E)，其中 V表示节点集，E是边集。执行去中心化共识的节点数量为p，若(i,j) ∈ E，则两个节点i和j互为邻居。存在由数据采集过程定义的m个目标函数。也就是说，网络中存在m个数据持有位置，各自拥有在网络中本地生成的数据。注意，当p= m时，每个节点i能够访问一个局部私有目标函数 Fi: R^n → R。目标是使每个节点都能获得最小化m个私有凸目标函数之和的全局最优解x ∈X。该问题描述如下：

$$
\min_{x \in X} \left{ F(x) := \sum_{i=1}^{m} F_i(x) \right}. \tag{1}
$$

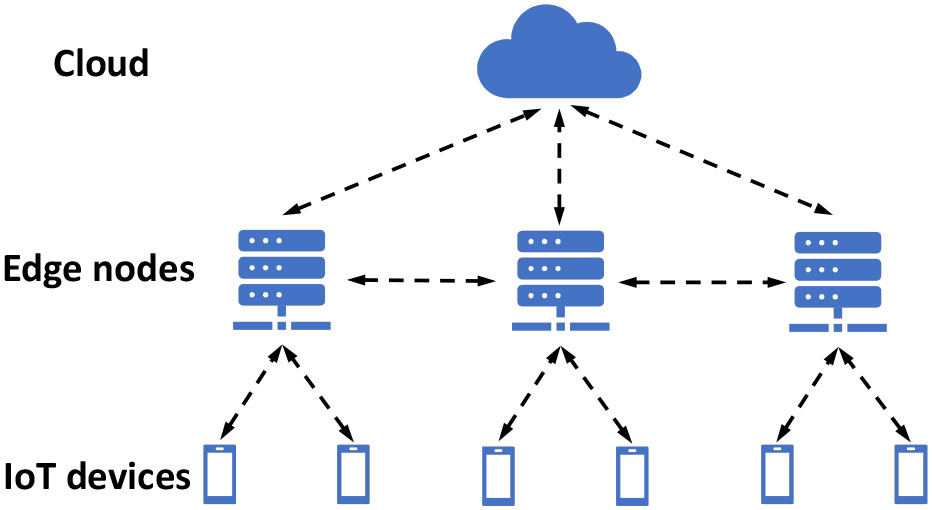
(1)中的公式在建模信号处理[17], 控制[18], 和统计学习[19]中的各种问题方面具有强大能力。函数Fi的示例包括最小二乘、逻辑回归、支持向量机等。相关应用已在文献中得到研究，例如电力系统、传感器网络、智能建筑和智能制造[20],[21]。在本研究中，我们提出了一种新型去中心化算法和一种混合协议，用于在边缘计算赋能的物联网网络[22]中求解(1)（见图1）。我们认为，这是对基于边缘计算的物联网网络中现有数据分析架构的重要补充。

第四节 算法

A. 去中心化算法设计

我们首先提出一种算法，旨在以完全去中心化的方式求解问题(1)。节点数量p设置为m，使得每个节点i可以访问一个数据存储位置，其中信息嵌入在局部私有目标函数Fi中。每个节点通过执行本地计算并与邻居通信来获得全局最优解。该所提出的去中心化算法的主要计算步骤如下：

$$
y_i^k = \theta x_i^{k-1} + (1 - \theta) x_i^{k-1}
$$
$$
x_i^k = P_X \left[ y_i^k - \alpha_{i,k} \tilde{\nabla} F_i(y_i^k) - \rho_{i,k} \left( \sum_{u \in N_i} \tilde{\nabla} F_u(x_u^{\tau_{u,k}}) \right) + \beta_{i,k}(x_i^{k-2}) \right] \tag{2}
$$

其中，k是虚拟全局迭代次数。Ni是节点i的邻居集合。$x_i^k$表示节点i在第k次迭代时的解决方案。$\tilde{\nabla} F_u(x_u^{\tau_{u,k}})$表示节点u在点$x_u^{\tau_{u,k}}$处的(次)梯度。$\tau_{u,k}$描述了可能过时的梯度信息。如果$\tau_{u,k}= k$，则$\tilde{\nabla} F_u(x_u^{\tau_{u,k}})$将是节点u的当前梯度。$P_X$是投影到可行域X上的投影算子。θ, αi,k, ρi,k和βi,k是算法的参数，将在后文上下文中进一步讨论。

该算法可总结如下。

注意，公式(2)中的第一个方程使用加权平均将节点i的解决方案与邻居节点ik的解决方案进行融合。该步骤主要用于推动所有节点就其对全局解的估计达成一致。公式(2)中的第二个方程是节点i的本地优化步骤，其中$y_i^k - \alpha_{i,k} \tilde{\nabla} F_i(y_i^k)$是使用节点i[23]拥有的Fi执行的常规梯度下降步骤。注意到[15]中提出的方案使用$y_i^k - \alpha_{i,k} \tilde{\nabla} F_i(y_i^k)$来更新$x_i^k$。在我们设计的公式(2)中的本地更新规则中，我们增加了两个额外的项。项$\sum_{u \in N_i} \tilde{\nabla} F_u(x_u^{\tau_{u,k}})$包含了节点i的邻居的梯度信息。结合项$y_i^k - \alpha_{i,k} \tilde{\nabla} F_i(y_i^k)$，它近似等效于使用多个节点的数据（多个Fi）执行梯度下降。在理想情况下，若节点i与系统中所有其他节点均为邻居，则节点i将直接优化公式(1)中的全局函数F，从而加快获得全局最优解的过程。最后一个项在

算法1 基于(2)的加速去中心化算法，其中p= m
输入：起始点 $x_1^0, x_2^0, \cdots, x_p^0$.
1: while 每个节点i，i ∈ {1, 2, …, p} 异步执行
2: 如果 (节点ik的本地时钟此刻滴答) 则
3: Node ik 广播 its 估计 $x_{ik}^{k-1}$ 和 (次)梯度 $\tilde{\nabla} F_i(x_{ik}^{k-1})$ 发送给其邻居；
4: 接收节点i广播的节点ik更新其基于(2)的解决方案 $x_i^k$
5: 结束如果
6: 结束循环

(2)的第二个方程 $(x_i^{k-1} - x_i^{k-2})$ 称为“动量”。动量项将历史信息引入当前估计中，以期找到更好的梯度方向，从而实现更快的收敛[16]。注意，参数αi,k, ρi,k和βi,k分别是上述各项的步长。

备注 1 ：在分布式/去中心化的计算框架中，计算与通信之间存在基本的权衡[24]。这意味着可以通过增加计算量来降低通信开销。在本研究中，考虑使用仅需计算函数值和梯度（而非海森矩阵，因为海森矩阵的计算成本高得多）的局部更新规则[，例如(2)]。我们的目标是让局部节点承担更多计算任务，以减少收敛所需的通信轮次。

B. 收敛性结果

本节展示了我们所提出的去中心化算法的收敛结果。收敛性分析所需的假设在假设1–3中进行了描述。

假设1 ：每个函数的有界（次）梯度Fi˜，使得‖∇Fi‖ ≤ G，其中G > 0为某个常数。

假设2 ：约束集X是有界的，使得该问题具有有限个解。

假设3 : $\sum_{k=1}^{\infty} \frac{\rho_{i,k}}{k \alpha_{i,k}} < \infty$, $\sum_{k=1}^{\infty} \frac{\beta_{i,k}}{k \alpha_{i,k}} < \infty$ 几乎必然。

定理1 : 由算法1为每个节点i生成的序列${x_i^k} \forall i \in V, k \geq 0$具有以下几乎必然的一致性性质：

$$
\sum_{k=1}^{\infty} \frac{1}{k} |x_i^{k-1} - \bar{x} {k-1}| < \infty, \quad \text{and} \quad \lim {k \to \infty} |x_i^k - \bar{x}_k| = 0
$$

其中 $\bar{x} {k-1} = \frac{1}{m} \sum {i=1}^{m} x_i^{k-1}$.

证明 : 详见附录B。

定理2 : 由算法1为每个节点i生成的序列${x_i^k} \forall i \in V, k \geq 0$几乎必然收敛到相同的最优解。

证明 : 详见附录C。

定理3 ：对于算法1，如果Fi是强凸的，则我们有以下结论：

$$
\frac{1}{T} \sum_{k=1}^{T} \left( \mathbb{E} \left[ \sum_{i=1}^{m} F_i(x_i^k) \right] \right) - F(x^ ) \leq O\left(\frac{\log T}{T}\right)
$$
$$
\frac{1}{T} \sum_{k=1}^{T} \left( \mathbb{E} \left[ \sum_{i=1}^{m} |x_i^k - x^ | \right] \right) \leq O\left(\frac{\log T}{T}\right).
$$

证明 ：详见附录D。

备注2 : 注意，假设1和2是分析分布式/去中心化算法[11]–[13]的常见条件。对于所提出的去中心化算法1，主要目标是使所有节点都能获得最优解。同时，我们也关注所有节点达到最优解的速度。定理1表明，每个节点最终都将收敛到所有节点的平均解，因此这意味着所有节点将在其估计值上达成一致。基于定理1，定理2确认了我们的目标可以实现，即所有节点将达到相同的最优解。该结论的推导首先证明某个特定节点能够达到最优解，然后应用所有节点将在其估计值上达成一致这一事实（定理1）。一般来说，定理3刻画了解误差（通过节点解与最优解之间的距离来表示）对迭代次数的依赖关系。它反映了所有节点在迭代次数意义上的最优解获取速度。

第五部分 实现：混合协议

在本节中，我们设计了一种混合去中心化协议，以在边缘计算架构（如图1所示）中实现并适配所提出的算法1。假设网络中有q个边缘节点正在运行去中心化分析。每个边缘节点负责其附近的物联网节点集合。假设每个物联网节点均为原始数据持有者，则物联网节点j可访问其私有目标函数Fj ∀j ∈ {1, 2,…,m}。物联网节点将计算其梯度，并将其发送至对应的边缘节点。随后，边缘节点之间将相互执行完全去中心化的算法，以获得全局最优解。由于边缘节点需要聚合其所属物联网节点的梯度，因此整个协议被认为是以混合去中心化方式执行的。该混合协议包含两部分：分别针对边缘节点和物联网节点的流程。这两部分总结于算法2和算法3中。

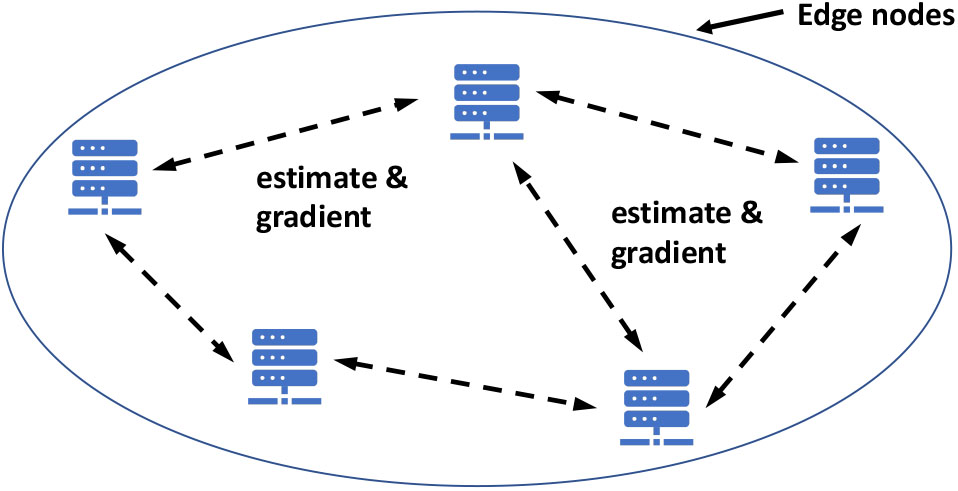
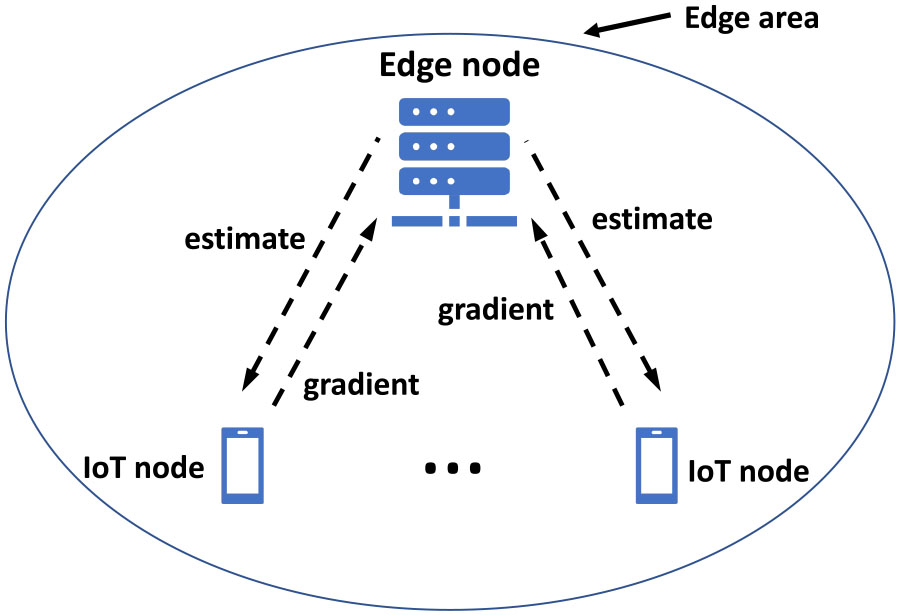
混合协议的去中心化部分在于边缘节点进行本地计算，并相互交换它们的估计值。该去中心化计算框架与算法1中描述的对应框架相同，并在图2中展示。注意，每个边缘节点与其物联网节点之间的交互采用基于聚合器的方案。边缘节点将其参数估计发送给其物联网节点，每个物联网节点使用其局部目标函数针对接收到的估计值计算梯度。这些计算出的梯度随后将返回至边缘节点进行聚合。此过程的示意图如图3所示。请注意，在我们的混合去中心化协议中，原始数据保留在所有物联网节点中（即数据生成的位置）。

边缘计算赋能的物联网网络中的混合去中心化数据分析

算法2 边缘节点过程

起始点 $x_1^0, x_2^0, \cdots, x_q^0$。初始化迭代次数 $k = 0$。
1: 当最大迭代次数未达到且最近两次估计之间的变化未在预设阈值内时，每个边缘节点 $i$ 异步执行以下操作：
2: 如果（节点 $i_k$ 的本地时钟触发）则
3: 边缘节点 $i_k$ 将其估计 $x_{i_k}^{k-1}$ 和 (次)梯度 $g_{i_k}^k$ 广播给其邻居；
4: 接收到边缘节点 $i_k$ 广播的边缘节点 $i$ 按如下方式更新其解决方案。
5: 边缘节点 $i$ 使用公式(2)中的第一个方程将其当前估计与 $x_{i_k}^{k-1}$ 混合。
6: 边缘节点 $i$ 将混合估计 $y_i^k$ 发送给其对应的物联网节点。
7: 边缘节点 $i$ 等待物联网节点返回它们的梯度，并将这些梯度聚合（求和）为 $g_i^k$。
8: 边缘节点 $i$ 基于公式(2)中的第二个方程更新其估计，将局部梯度 $\tilde{\nabla} F_i(y_i^k)$ 替换为 $g_i^k$（来自其物联网节点的聚合结果），并将邻居的(次)梯度 $\tilde{\nabla} F_u(x_u^{\tau_{u,k}})$ 分别替换为 $g_u^k$。
9: 结束如果
10: $k$ 递增。
11: 结束循环
12: 发送退出信号。

算法3 物联网节点过程

1: 当未接收到退出信号时，每个属于与边缘节点 $j$ 相关联的物联网节点集合的 $j$ 执行以下操作：
2: 物联网节点 $j$ 接收边缘节点 $i$ 的混合估计 $y_i^k$。
3: 物联网节点 $j$ 使用其局部目标函数 $F_j$ 在 $y_i^k$ 处计算梯度。
4: 物联网节点 $j$ 将其计算出的梯度发送给对应的边缘节点 $i$。
5: 结束循环

且从未被共享。在数据分析过程中，仅交换梯度和参数估计。

算法2和算法3中的信令开销和计算复杂度分析如下。假设系统中有 $m$ 个物联网节点（原始数据持有者）和 $p$ 个边缘节点。在每次迭代中，边缘节点会接收到 $O(1)$ 次广播和 $O(d)$ 条消息，其中 $d$ 是由边缘节点构成的网络的最大度（见图2）。具体而言，如果边缘节点构成一个网状网络，则 $d = p - 1$。每次通信的大小是决策向量大小的两倍（即 $x$）。对于边缘节点与其物联网节点之间的交互（见图3），在每次迭代中，最多有 $O(m)$ 次通信从物联网节点发送到对应的边缘节点，以及 $O(m)$ 次通信反向进行。每次通信的大小与决策向量的大小相同。关于计算复杂度，在每次迭代中并行执行 $O(d)$ 次边缘节点更新。其中 $d$ 是前述的最大度。每个边缘节点的更新涉及由其物联网节点执行的梯度评估。因此，每次迭代最多有 $O(m)$ 次梯度计算。

备注3 ：在某些实时性要求高的物联网应用中，需要尽快生成解决方案，我们可能无法等到边缘节点收敛。但在早期阶段，各边缘节点的估计值可能彼此不同，且难以确定哪一个更准确更好。因此，一种常见的策略是平均所有可用的估计值。

VI. 实验评估

A. 实验设置

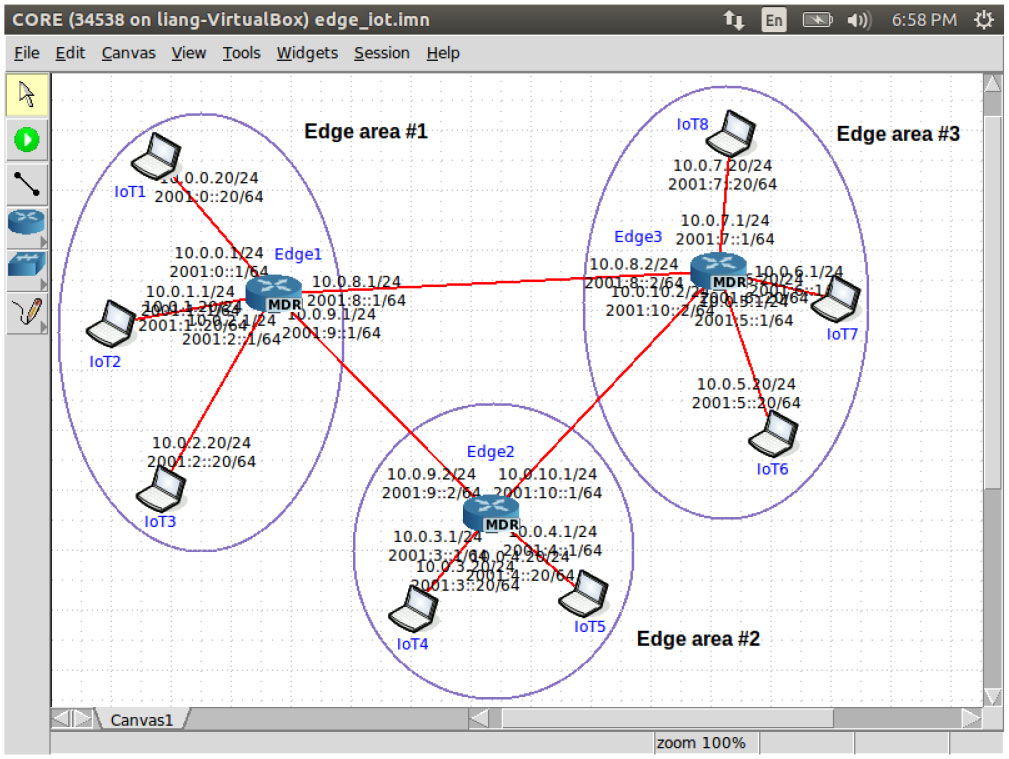
我们在两个应用上对我们提出的混合去中心化协议进行了实验：1）正则化最小二乘；2）计算机断层扫描。仿真在通用开放研究模拟器（CORE）中进行，该模拟器是一个分布式网络模拟器 [25]。所有实验均在配备 2.6 GHz 六核 Intel Core i7 处理器和 16 GB 内存的 MacBook Pro 上模拟。CORE 图形用户界面的一个示例如图4所示。关于协议中的参数[参见(1)]：1) 任何 $\theta \in [0, 1]$ 都是有效的，我们选择 $\theta = 0.5$ 作为本文所有测试中的“混合”参数；2) 局部梯度的步长 $\alpha_{i,k}$ 设置为边缘节点 $i$ 在迭代 $k$ 之前已完成的更新次数的倒数；3) 为了满足假设3，$\rho_{i,k}$ 和 $\beta_{i,k}$ 均简单地设为 $\alpha_{i,k}^2$。此外，我们将[15]中的两种去中心化算法（称为 Nedic）和[26]中的算法（称为 FDDA）适配到我们的混合架构中，并将我们提出的协议与它们进行比较。使用三个主要指标来测试和比较上述去中心化方法的收敛特性：目标值、相对误差和分歧。定义如下。

1) 目标值 ：$F(\bar{x} k)$，其中 $\bar{x}_k = \frac{1}{q} \sum {i=1}^{q} x_i^k$ 是所有边缘节点在第 $k$ 次迭代时的平均值。
2) 相对误差 ：$|\bar{x} k - x^ |_2 / |x^ |_2$，其中 $x^ $ 是由集中式求解器预先计算出的最优解。该指标用于跟踪所获得的平均解与最优解之间的距离。
3) 分歧 *：$\frac{1}{q} \sum {i=1}^{q} |x_i^k - \bar{x}_k|^2$。该指标用于衡量边缘节点在其估计值上的分歧程度。

、(b)和(c)中示出)

、(b)和(c)中示出)

B. 正则化最小二乘测试

我们首先在正则化最小二乘[27]的应用上测试所提出的混合协议，该问题是统计学、计算机科学和经济学中的常见问题[28]。正则化（蒂克霍诺夫正则化[29]）最小二乘问题的表述如下：

$$
\min_x \frac{1}{2} |Ax - b|_2^2 + \gamma |x|_2^2 \tag{3}
$$

其中 $A$ 是一个矩阵，其行通常表示数据。$b$ 是一个向量，$\gamma$ 是用于控制数据拟合项（第一项）和正则化部分之间权衡的正则化参数。为了将其融入我们的混合去中心化框架中，(3)被分解如下：

$$
\min_x \sum_{i=1}^{m} \left( \frac{1}{2} |A_i x - b_i|^2 + \frac{\gamma}{m} |x|_2^2 \right) \tag{4}
$$

因此，物联网节点 $i$ 的局部目标函数为

$$
F_i(x) = \frac{1}{2} |A_i x - b_i|^2 + \frac{\gamma}{m} |x|_2^2 \tag{5}
$$

在我们的网络设置中，我们在 50 个物联网节点（数据持有者，$m = 50$）和十个边缘节点上进行测试。每个边缘区域包含一个边缘节点和五个与之关联的物联网节点。对于所有边缘节点之间的连通性，分别测试了平均度为 3 和 5 的随机拓扑。矩阵 $A$ 被随机生成，大小为 $50 \times 80$。$A$ 和 $b$ 被均匀分解到所有节点，因此每个物联网节点拥有矩阵 $A$ 和向量 $b$ 的一行数据。矩阵 $A$ 和向量 $b$ 中的每个元素在 $[0, 1)$ 上均匀采样。正则化参数 $\gamma$ 设为 1。

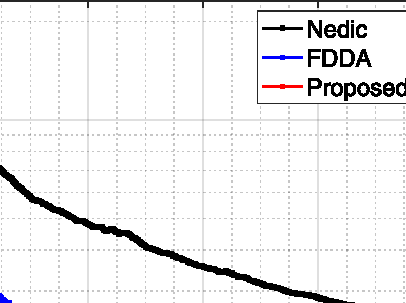
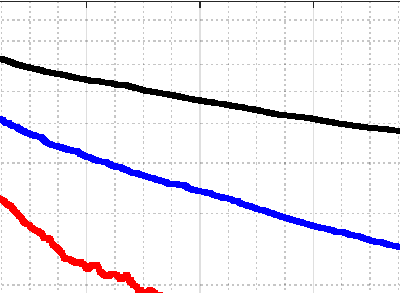
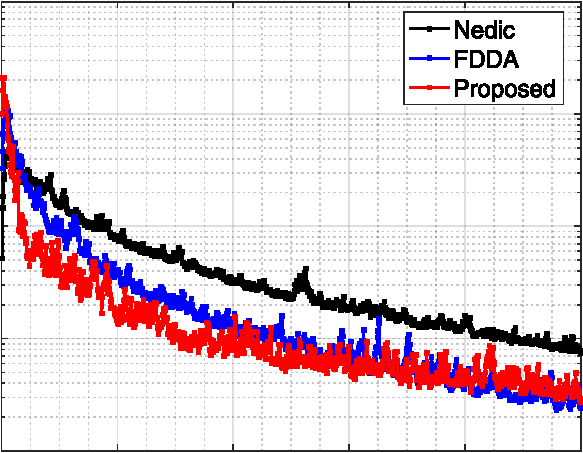
实验结果如图5–7所示。从图5和图6可以看出，与基准方法相比，我们提出的协议在平均目标值的收敛速度、相对误差（精度）以及所有边缘节点之间的估计分歧方面均表现更优。比较图5和图6可知，当边缘节点之间的连接性更高（平均度从3增加到5）时，所有方法都能更快地达到相同的精度。这证明了连接性在去中心化算法中的影响。此外，请注意在估计分歧的指标中，所有边缘节点（同一边缘区域内的物联网节点与其边缘节点具有相同的估计值），更高的连接性可平滑波动。这是符合预期的，因为更高的连接性可以加快去中心化环境中的信息传播速度。图7展示了每个边缘节点与其他邻居交换的消息情况。注意，在两种情况下（度数为3和5），所有节点之间的通信都是均衡的，这是去中心化算法的特征之一。此外，可以观察到，在更高连接性的设置下，每个边缘节点会交换更多的消息，因为它们可以从更多的邻居接收消息。

C. 计算机断层扫描测试

本节中，我们对所提出的协议在计算机断层扫描[30]中的应用进行实验。我们使用 AIR 包[31]中的代码进行此测试。通过平行束生成一个二维断层扫描测试问题。为简便起见，我们采用模型(3)来重建该断层扫描图像。在测试问题中，断层扫描的维度为 $50 \times 50$（图像分辨率），矩阵 $A$ 的大小为 $5400 \times 2500$，原始向量 $b$ 添加了 5% 的随机噪声以构造“含噪”问题。本次测试中的边缘区域数量为 10。每个边缘节点的邻居是随机生成的，每个节点的平均度为 5。每个边缘区域包含十个物联网节点，每个物联网节点在矩阵 $A$ 中包含 54 行数据。

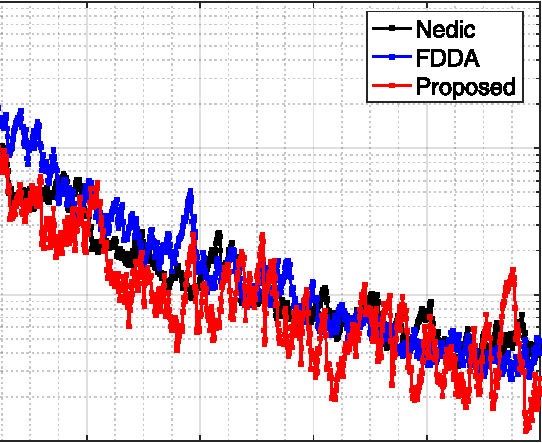
实验结果如图8–10所示。图8再次表明，我们提出的混合协议在获取网络中所有节点的全局最优解的速度方面优于其他基准方法。图9展示了二维测试问题的断层扫描结果，可以观察到我们的去中心化解法在视觉上接近其集中式对应解法。需要注意的是，由于添加了噪声，集中式解法[图9(b)]与真实值[图9(a)]并不完全相同。用于重建断层图像的重建模型会影响我们得到的断层扫描结果与真实值之间的对比，而如何设计重建模型超出了本论文的研究范围。我们的目标是通过所提出的混合去中心化协议。

真实值。(b) 集中式解法。(c) 提出的方法在第500次迭代时的结果)

在图10中，我们分别对每个边缘节点的收敛性能进行了更详细的观察。可以看出，经过大约60次迭代后，所有边缘节点的估计值彼此非常接近，这是一个理想的特性，因为我们可以选择任意一个边缘节点的估计值作为最终解决方案，因为它们都是共识的。在图10背后需要注意的是，每次迭代中物联网节点并行执行了50次梯度评估。这是因为在每次迭代中选出了五个边缘节点进行更新，而每个边缘区域包含十个物联网节点。

D. 逻辑回归测试

在本节中，我们对逻辑回归任务进行测试，以进一步证明我们去中心化协议的适用性。我们使用安然电子邮件数据集[32]并训练一个逻辑回归模型，将邮件分类为垃圾邮件或非垃圾邮件。该任务可以表述为如下形式的去中心化优化问题：

$$
\min_x \sum_{i=1}^{m} \sum_{j=1}^{m_i} \log(1 + \exp(-b_j^i (A_j^i)^T x)) \tag{6}
$$

由物联网节点 $i$ 持有的局部目标函数是

$$
F_i(x) = \sum_{j=1}^{m_i} \log(1 + \exp(-b_j^i (A_j^i)^T x)) \tag{7}
$$

其中 $m_i$ 是物联网节点 $i$ 拥有的实例数量。$b_j^i$ 是向量 $b_i$ 的第 $j$ 个元素，该向量包含第 $i$ 个物联网节点的二元结果。类似地，$(A_j^i)^T$ 表示矩阵 $A_i$ 的第 $j$ 行。$A_i$ 中的每一行代表一个实例，列表示特征变量。我们使用前两个文件夹

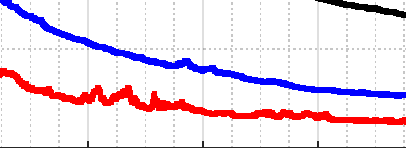
在此场景中，前 5000 封电子邮件用于训练，其余 6029 封用于测试。电子邮件经过预处理，并保留 7997 个高频词作为特征。关于边缘计算环境的设置，使用了 100 个物联网节点（$m = 100$）和十个边缘节点。每个边缘区域包含十个物联网节点。每个边缘节点的直接邻居数量设置为 5。原始数据被均匀分配到各个物联网节点，因此每个节点包含 50 条记录（$m_i = 50$）。因此，$A_i$ 和 $b_i$ 的维度分别为 $50 \times 7997$ 和 $50 \times 1$。实验结果如图11所示。采用对数损失和分类错误率来衡量模型性能。使用十个边缘节点的平均模型分别捕获所提出的去中心化分析过程在训练和测试数据集上的特性。可以看出，在大约 20 次迭代后，训练和测试的错误率均低于 0.02（精度为 0.98）。

VII. 结论

随着物联网设备的大规模部署，传统的基于云的解决方案由于三个主要限制而不再适用于相关的物联网数据分析任务：1）大量的数据迁移；2）高延迟；以及3）有限的隐私保护。边缘计算作为一种有前景的基础设施出现在物联网网络中，但构建数据分析管道需要精心设计。我们提出了一种面向边缘计算赋能的物联网网络的混合去中心化框架，旨在解决上述所有问题。理论分析和实验评估表明，所提出的方法能够在原始数据本地化的情况下提供高效的数据分析。可能的未来工作包括研究新的分析方法以放宽去中心化方案中的条件（如假设1），以及嵌入其他隐私保护技术以进一步提升框架的隐私保护水平。