python排序算法（一）、冒泡排序、选择排序、插入排序

原创已于 2022-09-11 10:45:43 修改 · 434 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#排序算法 #算法 #python

于 2022-09-03 14:30:40 首次发布

数据结构专栏收录该内容

7 篇文章

订阅专栏

本文详细介绍了三种基本的排序算法：冒泡排序、选择排序和插入排序，并提供了Python代码实现。通过示例展示了每种排序算法的运作过程，同时分析了它们的时间复杂度。此外，还通过实际运行时间对比了这三种排序算法在处理大量数据时的效率差异。

排序：将一组”无序“的记录序列调整为”有序”的记录序列

列表排序：将无序列表变为有序列表

输入：列表
输出：有序列表

升序和降序

内置排序函数：sort()

1、冒泡排序

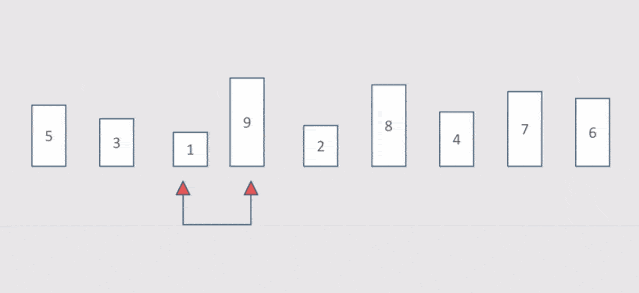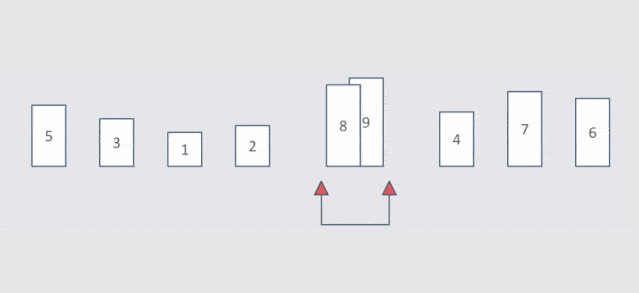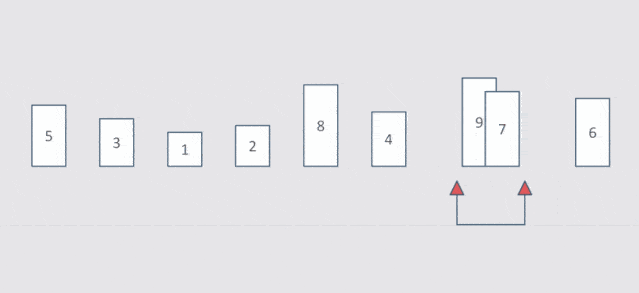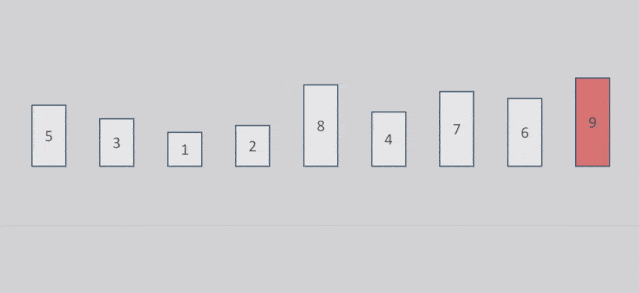
列表每两个相邻的数，如果前面比后面大，则交换这两个数
一趟排序完成后，则无序区减少一个数，有序区增加一个数
代码关键点：
- 趟
- 无序区范围

示意图

代码

def bubble_sort(li):
    for i in range(len(li) - 1):  # 趟数（n-1）
        for j in range(len(li) - i - 1):
            if li[j] > li[j + 1]:
                li[j], li[j + 1] = li[j + 1], li[j]
        print("第%s趟" % i, li)


li = [9, 8, 7, 1, 2, 3, 4, 5, 6]
print(li)
bubble_sort(li)


# 结果

[9, 8, 7, 1, 2, 3, 4, 5, 6]
第0趟 [8, 7, 1, 2, 3, 4, 5, 6, 9]
第1趟 [7, 1, 2, 3, 4, 5, 6, 8, 9]
第2趟 [1, 2, 3, 4, 5, 6, 7, 8, 9]
第3趟 [1, 2, 3, 4, 5, 6, 7, 8, 9]
第4趟 [1, 2, 3, 4, 5, 6, 7, 8, 9]
第5趟 [1, 2, 3, 4, 5, 6, 7, 8, 9]
第6趟 [1, 2, 3, 4, 5, 6, 7, 8, 9]
第7趟 [1, 2, 3, 4, 5, 6, 7, 8, 9]

由结果看出，不管是有序列表还是无序列表，该冒泡排序代码，都会排序n-1次，所以我们可以改进代码，在当排序时无序区没有发生改变，我们可以认为此时已经排序完成

时间复杂度：

O（n²）

代码改进

def bubble_sort(li):
    for i in range(len(li) - 1):
        exchange = False
        for j in range(len(li) - i - 1):
            if li[j] > li[j + 1]:
                li[j], li[j + 1] = li[j + 1], li[j]
                exchange = True
        print("第%s趟" % i, li)
        if exchange is False:
            return


li = [9, 8, 7, 1, 2, 3, 4, 5, 6]
print(li)
bubble_sort(li)


# 结果
[9, 8, 7, 1, 2, 3, 4, 5, 6]
第0趟 [8, 7, 1, 2, 3, 4, 5, 6, 9]
第1趟 [7, 1, 2, 3, 4, 5, 6, 8, 9]
第2趟 [1, 2, 3, 4, 5, 6, 7, 8, 9]
第3趟 [1, 2, 3, 4, 5, 6, 7, 8, 9]

2、选择排序

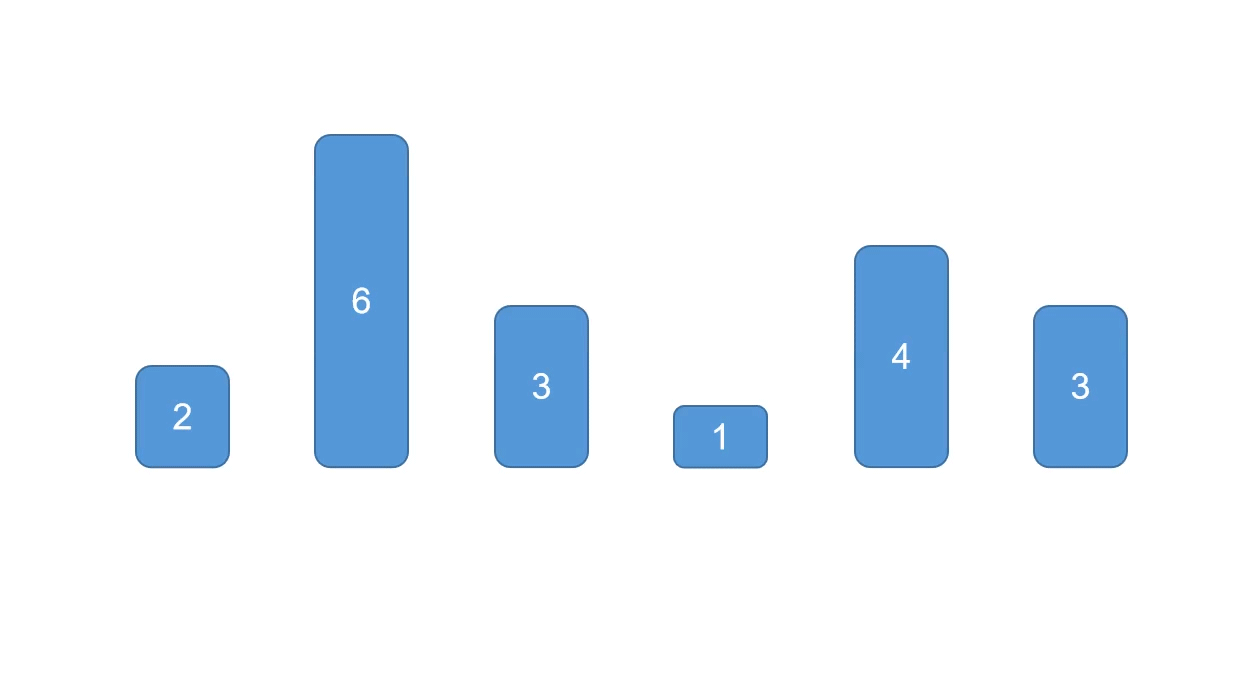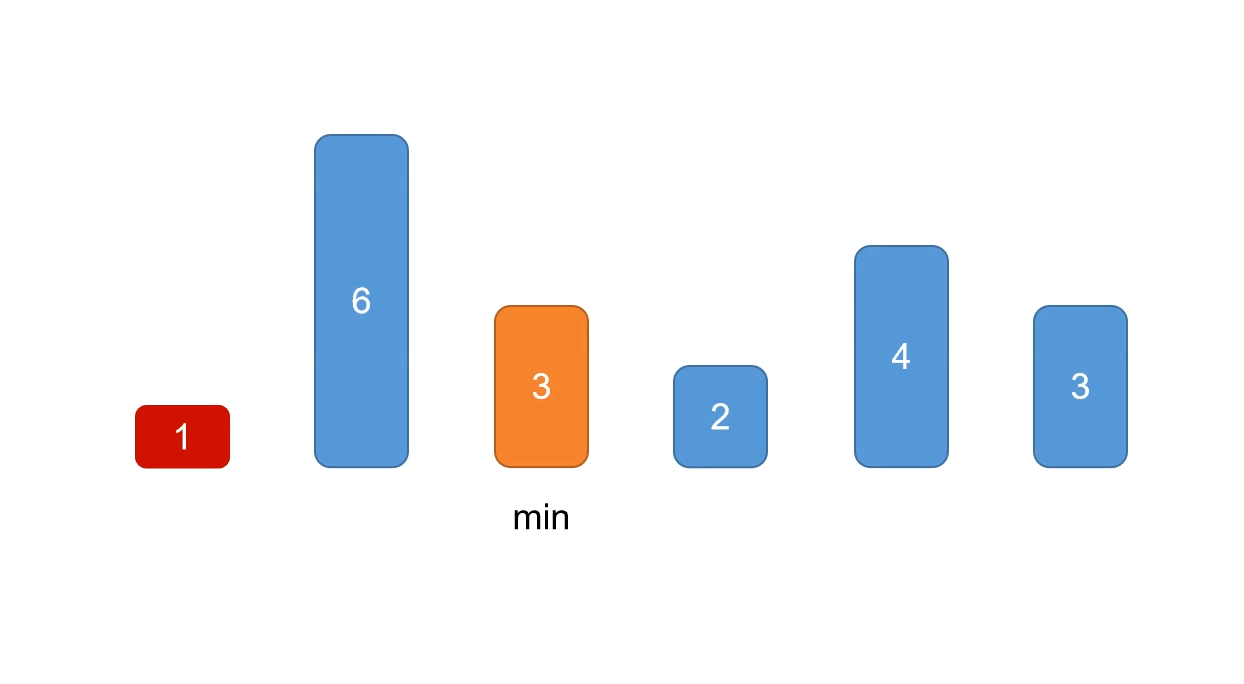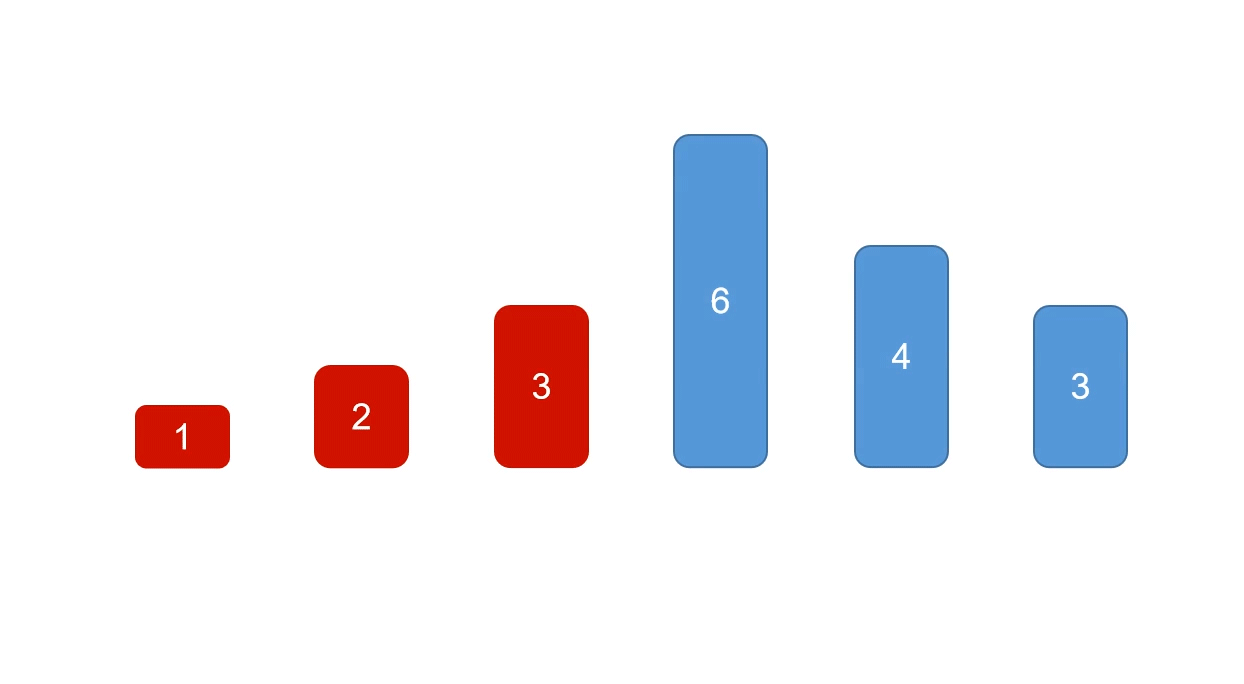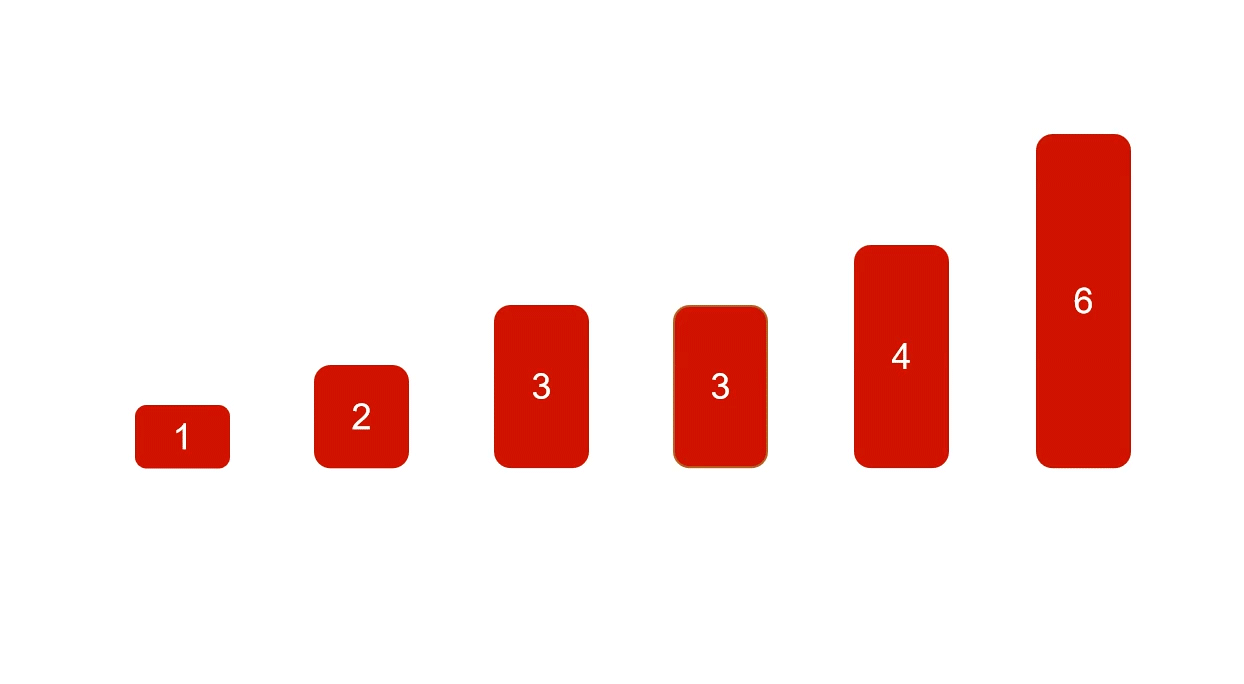
循环遍历列表list，每次遍历将当前遍历出来的元素i与i后面的所有元素进行比较，取最小值min,然后将min与i交换位置，遍历所有元素后，即达成排序效果

代码

def select_sort(li):
    for i in range(len(li) - 1):
        min_loc = i  # 将每次遍历出来的下标记录为最小位置
        for j in range(i + 1, len(li)):  # 把上面记录的最小位置的值，与之后面所有的值进行比较，取最小值
            if li[j] < li[min_loc]:
                min_loc = j
        li[i], li[min_loc] = li[min_loc], li[i]
        print(li)


li = [6, 3, 4, 5, 7, 2, 1, 9, 8]
print(li)
select_sort(li)
print(li)


# 结果
[6, 3, 4, 5, 7, 2, 1, 9, 8]
[1, 3, 4, 5, 7, 2, 6, 9, 8]
[1, 2, 4, 5, 7, 3, 6, 9, 8]
[1, 2, 3, 5, 7, 4, 6, 9, 8]
[1, 2, 3, 4, 7, 5, 6, 9, 8]
[1, 2, 3, 4, 5, 7, 6, 9, 8]
[1, 2, 3, 4, 5, 6, 7, 9, 8]
[1, 2, 3, 4, 5, 6, 7, 9, 8]
[1, 2, 3, 4, 5, 6, 7, 8, 9]
[1, 2, 3, 4, 5, 6, 7, 8, 9]

时间复杂度：

O（n²）

3、插入排序

插入排序的工作方式像许多人排序一手扑克牌。开始时，我们的左手为空并且桌子上的牌面向下。然后，我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置，我们从右到左将它与已在手中的每张牌进行比较。拿在左手上的牌总是排序好的。

插入排序是指在待排序的元素中，假设前面n-1(其中n>=2)个数已经是排好顺序的，现将第n个数插到前面已经排好的序列中，然后找到合适自己的位置，使得插入第n个数的这个序列也是排好顺序的。按照此法对所有元素进行插入，直到整个序列排为有序的过程，称为插入排序

代码

def insert_sort_two(li):
    for j in range(1, len(li)):  # j 代表我手里摸到牌的下标
        tmp = li[j]  # 当前摸到的牌
        k = j - 1  # k代表我手里现在最右边的牌（0，j-1）
        # 找到排序的位置插入当前摸到的牌（将手里的牌依次与摸到的牌进行比较，如果手里的牌大于摸到的牌，则手里的牌向后移一位）
        while k >= 0 and li[k] > tmp: 
            li[k + 1] = li[k]
            k -= 1
        li[k + 1] = tmp

li = [4, 2, 1, 3, 7, 5, 9, 8, 6]
insert_sort(li)


# 结果
[2, 4, 1, 3, 7, 5, 9, 8, 6]
[1, 2, 4, 3, 7, 5, 9, 8, 6]
[1, 2, 3, 4, 7, 5, 9, 8, 6]
[1, 2, 3, 4, 7, 5, 9, 8, 6]
[1, 2, 3, 4, 5, 7, 9, 8, 6]
[1, 2, 3, 4, 5, 7, 9, 8, 6]
[1, 2, 3, 4, 5, 7, 8, 9, 6]
[1, 2, 3, 4, 5, 6, 7, 8, 9]

时间复杂度：

O(n²)

4、比较三个排序算法

import random

import time


def cal_time(func):
    def inner(*args, **kwargs):
        strat = time.time()
        result = func(*args, **kwargs)
        end = time.time()
        print('%s执行时间:%s' % (func.__name__, end - strat))
        return result

    return inner




@cal_time
def bubble_sort(li):
    for i in range(len(li) - 1):
        exchange = False
        for j in range(len(li) - i - 1):
            if li[j] > li[j + 1]:
                li[j], li[j + 1] = li[j + 1], li[j]
                exchange = True
        # print("第%s趟" % i, li)
        if exchange is False:
            return

@cal_time
def select_sort(li):
    for i in range(len(li) - 1):
        min_loc = i  # 将每次遍历出来的下标记录为最小位置
        for j in range(i + 1, len(li)):  # 把上面记录的最小位置的值，与之后面所有的值进行比较，取最小值
            if li[j] < li[min_loc]:
                min_loc = j
        li[i], li[min_loc] = li[min_loc], li[i]
        # print(li)




@cal_time
def insert_sort(li):
    for j in range(1, len(li)):  # j 代表我手里摸到牌的下标
        tmp = li[j]  # 当前摸到的牌
        k = j - 1  # k代表我手里现在最右边的牌（0，j-1）
        # 找到排序的位置插入当前摸到的牌（将手里的牌依次与摸到的牌进行比较，如果手里的牌大于摸到的牌，则手里的牌向后移一位）
        while k >= 0 and li[k] > tmp:
            li[k + 1] = li[k]
            k -= 1
        li[k + 1] = tmp
        # print(li)


li = list(range(1, 10000))
random.shuffle(li)
bubble_sort(li)
select_sort(li)
insert_sort(li)

bubble_sort执行时间:3.270739793777466
select_sort执行时间:1.2142643928527832
insert_sort执行时间:0.0