LeetCode刷题：212. 单词搜索 II （golang版）

• 题目描述

给定一个 m x n 二维字符网格 board 和一个单词（字符串）列表 words，找出所有同时在二维网格和字典中出现的单词。

单词必须按照字母顺序，通过 相邻的单元格 内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。

 
示例 1：
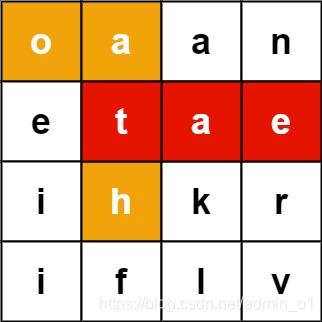
输入：board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
输出：["eat","oath"]

示例 2：
输入：board = [["a","b"],["c","d"]], words = ["abcb"]
输出：[]
 
提示：
m == board.length
n == board[i].length
1 <= m, n <= 12
board[i][j] 是一个小写英文字母
1 <= words.length <= 3 * 104
1 <= words[i].length <= 10
words[i] 由小写英文字母组成
words 中的所有字符串互不相同

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/word-search-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

• 思路
  1、跟单词搜索 I不同的是处理的数据多了，所以不能再用之前的方法简单的为每个单词进行深度搜索然后汇总，会超时
  2、用前缀树tria，先将单词构建成一颗trial树，然后进行处理

• 代码

package main

import (
	"fmt"
)
//前缀树结构，注意childres是map，这样才能用O(1)时间查找到孩子节点
type Tria struct{
	childres map[string]*Tria
	isWord bool
}

func findWords(board [][]byte, words []string) []string {
	//先构建tria树
	var root = new(Tria)
	rootb := root
	//遍历单词切片
	for _,v := range words {
		//根节点地址另存一份，每个单词在构建tria时都要用
		root = rootb
		//单词字符串，将每个字符串字符填入前缀树中
		for _,v2 := range v {
			if root.childres[string(v2)] == nil {
				tmp := new(Tria)
				if root.childres == nil {
					root.childres = make(map[string]*Tria)
				}
				root.childres[string(v2)] = tmp
			}
			root = root.childres[string(v2)]
		}
		//标记到此为止是个单词
		root.isWord = true
	}

	//开始处理
	var (
		//log保存状态位，true代表已被使用过
		log [12][12]bool
		str string
		//因为单词可能有重复的，所有先存在map中去重，再将map转为切片返回
		res = make([]string,0)
		resM = make(map[string]bool)
	)
	//遍历board，每个符合第一个单词前缀的格子都进行递归处理
	for i:=0; i<len(board); i++ {
		for j:=0; j<len(board[0]); j++ {
			if  rootb.childres[string(board[i][j])] != nil {
				DFS(&board,rootb,log,i,j,str,&resM)
			}
		}
	}
	//转为题目要求的切片类型
	for k,v := range resM {
		if v == true {
			res = append(res,k)
		}
	}
	return res
}

//深度优先遍历，log是标志位，true代表已被使用过，rowI和colI是行列下标，str是前缀字符串，resM保存符合要求的单词
func DFS(board *[][]byte, root *Tria, log [12][12]bool, rowI int,colI int,str string,resM *map[string]bool) {

	var (
		row = len(*board)
		col = len((*board)[0])
	)
	//递归终止条件，下标越界或已被使用过，不符合要求，终止递归
	if colI >= col || colI < 0 || rowI >= row || rowI < 0 || log[rowI][colI] == true {
		return
	}
	//当前节点不存在该字符，不符合要求，终止递归
	if root.childres[string((*board)[rowI][colI])] == nil {
		return
	}
	//符合要求，将前缀树字符转为字符串Word
	str += string((*board)[rowI][colI])
	//通过标志位isWord判断是否为单词，若是则保存到resM中
	if root.childres[string((*board)[rowI][colI])].isWord == true {
		(*resM)[str] = true
	}
	//将该位置标为已被使用过
	log[rowI][colI] = true
	//依次处理当前位置的上下左右位置
	DFS(board,root.childres[string((*board)[rowI][colI])],log,rowI+1,colI,str,resM)
	DFS(board,root.childres[string((*board)[rowI][colI])],log,rowI-1,colI,str,resM)
	DFS(board,root.childres[string((*board)[rowI][colI])],log,rowI,colI+1,str,resM)
	DFS(board,root.childres[string((*board)[rowI][colI])],log,rowI,colI-1,str,resM)
}


func main() {
	var tmp  = []byte{'o','a','b','n'}
	var t [][]byte
	t = append(t,tmp)

	tmp  = []byte{'o','t','a','e'}
	t = append(t,tmp)
	tmp  = []byte{'a','h','k','r'}
	t = append(t,tmp)

	tmp  = []byte{'a','f','l','v'}
	t = append(t,tmp)

	words := []string{"oa","oaa","ot","ah"}
	res := findWords(t,words)
	fmt.Println(res)
}