二分查找详解

二分查找详解

标准代码

//【left,right】
public int search(int[] nums, int target) {
    // 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算
    if (target < nums[0] || target > nums[nums.length - 1]) {
        return -1;
    }
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + ((right - left) >> 1);
        if (nums[mid] == target)  return mid;
        else if (nums[mid] < target)  left = mid + 1;
        else if (nums[mid] > target)  right = mid - 1;
    }
    return -1;
}

//【left,right)
public int search(int[] nums, int target) {
    int left = 0, right = nums.length;
    while (left < right) {
        int mid = left + ((right - left) >> 1);
        if (nums[mid] == target)
            return mid;
        else if (nums[mid] < target)
            left = mid + 1;
        else if (nums[mid] > target)
            right = mid;
    }
    return -1;
}

代码易混淆点

我们在写代码的时候经常会对

while (left <= right)

这个while循环中的判断条件（小于还是小于等于合适呢？）感到疑惑

这需要看我们二分查找的区间是什么形式的

如果我们的区间是 左闭右闭的如下

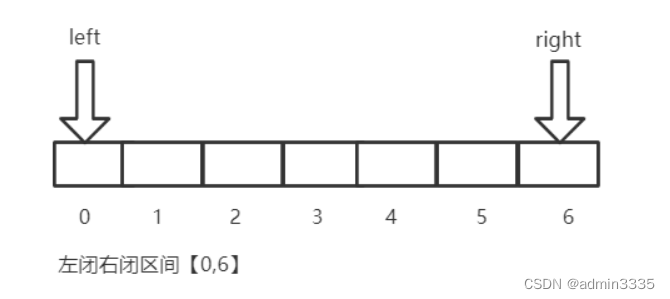
那left在等于right的情况下也是在【0，6】这个区间内是有意义的

当区间为左闭右开时

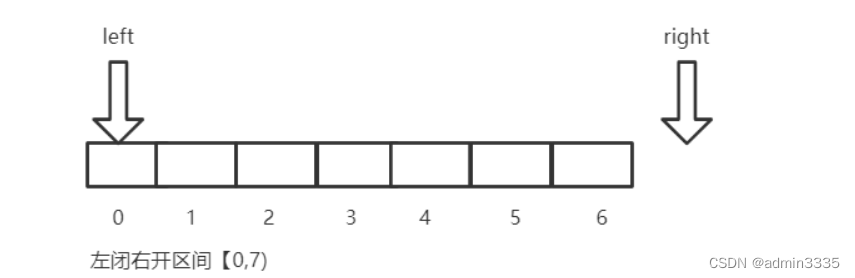
此时如果left等于right就可能出现问题了，那就是：

如果目标值比数组中下标为6的数大，那left会一直向右移动。如果此时是left<=ringht的话

mid=(left+right)/2=(0+7)/2=4 nums[mid]<target left=mid+1=5 此时搜查区间为【5，7)

mid=(left+right)/2=(5+7)/2=6 nums[mid]<target left=mid+1=7 此时搜查区间为【7，7)

mid=(left+right)/2=(7+7)/2=7 nums[mid]出现了越界的情况

或者说【7，7）这个区间根本没有任何意义

而left<right就不会出现问题了

其次是对于

if (nums[mid] == target)  return mid;
else if (nums[mid] < target)  left = mid + 1;
else if (nums[mid] > target)  right = mid - 1;

究竟是left=mid还是left=mid+1?

对于左闭右闭 left = mid + 1 ; right = mid - 1;因为mid一定都是在区间内的nums[mid] < target，nums[mid] > target时mid下标下的数字已经被比较了

此时区间变为【left,mid-1】或【 right = mid - 1，right】加上mid已经做了比较，因此没有落下一个元素。

对于左闭右开 left = mid + 1 ; right = mid;由于左边时闭区间，因此left每次移动时mid下标下的数据都参与了比较。而右边是开区间，因此搜索区间变为

【left,mid)此时right = mid就相当于左闭右闭的right = mid - 1了。

我们要记住一开始是是什么样开闭的区间，划分区间后也应该是什么样开闭的区间