这是一道很好的最短路的题目
难点
1.如何建图。
2.如何进行更新最短路。
3.求最小方案。
建图
输入中有药水的配置:
A + B = C
1 2 0
4 5 1
3 6 2
这看上去是不是很像图论?
选用链式前向星。
如下:
int head[1010],cnt;
void add(int u,int v,int w){
E[++cnt].to = v;
E[cnt].w = w;
E[cnt].next = head[u];
head[u] = cnt;
}
和:
int u,v,w;
while(scanf("%d%d%d",&u,&v,&w)!=EOF){
add(u,v,w);
if(u==v) continue;
add(v,u,w);
}
诶,这看上去和模板也没什么区别啊?
先放下建图。
求最小方案数
用 cost 数组记录某药水的最小值,ans 数组记录某药水的方案数量。
cost 初始化为商店药水原价,ans 初始化为 1 1 1 (题目中:直接买 0 0 0 号药水)。
诶?多少种不同的花费最少的方案?乍看上去好难啊,但细细想想还是挺简单的,来,上图!!!(这不是本题的建图,只是为了方便理解)
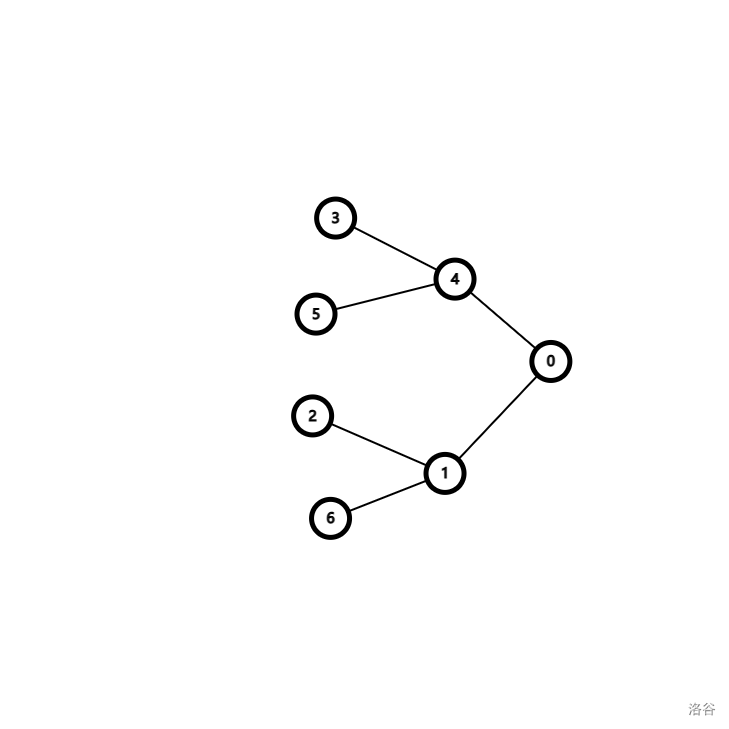
假设配置 4 有两种方案, 3 − > 4 3 -> 4 3−>4 和 5 − > 4 5 -> 4 5−>4 ,配置 1 1 1 有两种方案 2 − > 1 2 -> 1 2−>1 和 6 − > 1 6 -> 1 6−>





 本文详细解析了一道涉及最短路算法的题目,通过链式前向星建图,使用Dijkstra更新最短路,求解配置魔法药水的最小方案数。通过举例说明了如何计算不同花费的最小方案,并给出了AC代码。
本文详细解析了一道涉及最短路算法的题目,通过链式前向星建图,使用Dijkstra更新最短路,求解配置魔法药水的最小方案数。通过举例说明了如何计算不同花费的最小方案,并给出了AC代码。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 814
814

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








