【P4551 最长异或路径】

P4551 最长异或路径

题目描述

给定一棵 $n$ 个点的带权树，结点下标从 $1$ 开始到 $n$。求树中所有异或路径的最大值。

异或路径指树上两个结点之间唯一路径上的所有边权的异或值。

输入格式

第一行一个整数 $n$，表示结点数。

接下来 $n-1$ 行，给出 $u,v,w$ ，分别表示树上的 $u$ 点和 $v$ 点有连边，边的权值是 $w$。

输出格式

一行，一个整数表示答案。

输入输出样例 #1

输入 #1

4
1 2 3
2 3 4
2 4 6

输出 #1

7

说明/提示

当两个结点分别是 $1,3$ 时，答案是 $7=3\oplus 4$，取最大值。

数据范围

$1\le n\le 10^5;0<u,v\le n;0\le w<2^{31}$。

前缀和

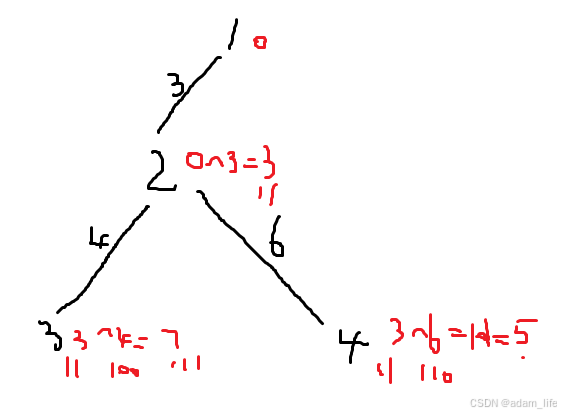
1.树，无环，所以任意节点都可以是根
2.现在求的是"树上两个结点之间唯一路径上的所有边权的异或值"，如节点1^节点2^节点3^节点4，现在"异或路径的最大值"其实就是节点1到节点3间的异或值是7。
3.现在任意选一个点为根，这里方便期间选的是1，求前缀异或和，就是各节点到1的异或和，这个可以pre_xor[1]=0,
pre_xor[2]=pre_xor[1]^3,
pre_xor[3]=pre_xor[2]^4,
pre_xor[4]=pre_xor[4]^6。
这个过程可以用宽搜完成。O(n)
4.前缀和间的异或就是最大异或值，这里就是pre_xor[3]^pre_xor[0]=7。

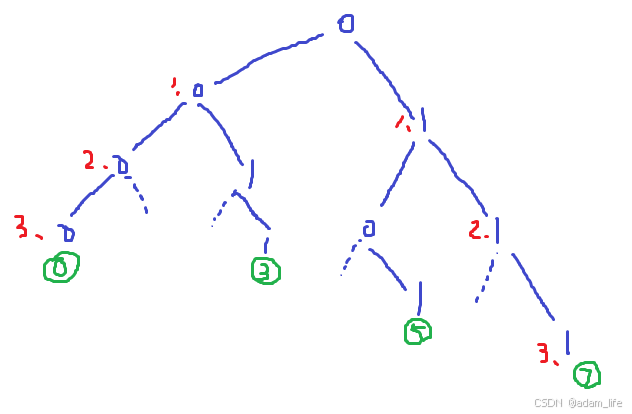
5.把各节点到根节点的前缀异或和写成01字典树，共32层，从根往下是对应的二进制，每层都是其中一位二进制，能表示所有的int(高位自然是0)。那这些数间的最大异或值，只需找最大异或对，就是两前缀和的32层每层都尽量是相反数，而且尽量满足高位相反。O(32n)
6.O(n+32n),远优于暴力(n²)

代码

#include <bits/stdc++.h>
using namespace std;
struct node{//字典树节点
node *l,*r;//左右子节点
node():l(NULL),r(NULL){}//构造函数
};
class trie{//字典树类
private://私有变量和函数
int max_xor;//两个结点之间唯一路径上的所有边权的异或值。
node *root;//根节点
void destroy(node cur){//销毁占有内存
if(cur->l)destroy(cur->l);//先销毁子节点
if(cur->r)destroy(cur->r);
delete cur;//再删除该节点
}
public:
trie(){max_xor=0;root=new node();}//类构造函数
~trie(){destroy(root);}//析构函数
void insert_query(int x){//插入每个节点到根节点的前缀异或和
/
求所有节点间唯一路径上所有边权的异或值。
到根节点前缀异或和间的异或
到根节点的公共祖先部分会抵消——a^a=0，只剩节点间的路径部分的异或值
*/
int cur_xor=0;//初始异或
node *cur=root,*oth=root;//本前缀和在字典树中的位置和相反前缀和节点位置。a!=b
for(int i=31;i>=0;i–){//存够32层，能表示所有int
int bit=(x>>i&1);//取出x的第i位二进制数(i变小就是从高位开始)
if(bit){//1表示接右树
if(!cur->r)cur->r=new node();//没右节点就建立
cur=cur->r;//到下层
if(oth->l){//相反数就得左树0
cur_xor|=(1<<i);//结果的第i位要保证是1
oth=oth->l;//相反数找下一层
}else if(oth->r)oth=oth->r;//没左节点就只好右节点，原i位数二进制不变
else oth=NULL;
}else{//0表示接左树
if(!cur->l)cur->l=new node();
cur=cur->l;
if(oth->r){
cur_xor|=(1<<i);
oth=oth->r;
}else if(oth->l)oth=oth->l;
else oth=NULL;
}
}
max_xor=max(max_xor,cur_xor);//得到最大前缀异或和间异或值
}
int getans(){return max_xor;}
void view(){//层数遍历打印字典树
node cur=root;//当前节点初始是根节点
int cur_level=0,bit,level;//层数深度和当前深度
queue<pair<node,pair<int,int>>> q;//宽搜队列，三元素：节点、左右和深度
q.push({cur,{-1,0}});//根节点放进队列
while(!q.empty()){//非空就宽搜
cur=q.front().first,bit=q.front().second.first,level=q.front().second.second;q.pop();//当前节点、左右类型、深度
if(cur_level<level){//换深度，输出换行
cout<<endl;cur_level=level;
}
if(bit==-1)cout<<“root\t”;//输出根
else if(bit)cout<<“1\t”;//右树
else cout<<“0\t”;//左树
if(cur->r)q.push({cur->r,{1,level+1}});//递归右子树
if(cur->l)q.push({cur->l,{0,level+1}});//递归左子树
}
}
}t;
const int N=1e5+1;
int n,
u,v,w,//两节点间权值
pre_xor[N];//前缀和
vector<pair<int,int>> adj[N];//每个节点连接的节点和权值
queue q;//宽搜队列
int main(){
//freopen(“data.cpp”,“r”,stdin);
cin>>n;
for(int i=1;i<n;i++){//遍历n-1个边
cin>>u>>v>>w;
adj[u].push_back({v,w});//u出发的终点和权值
adj[v].push_back({u,w});//双向
}
q.push(1);pre_xor[1]=0;t.insert_query(pre_xor[1]);//根节点出发，把根节点放进字典树
while(!q.empty()){//宽搜遍历所有节点，计算到各节点的前缀异或和
u=q.front();q.pop();//出发点
for(int i=0;i<adj[u].size();i++){//遍历u点出发的所有终点
v=adj[u][i].first;
w=adj[u][i].second;
if(!pre_xor[v]&&v!=1){//如果没计算过，而且非根节点
pre_xor[v]=pre_xor[u]^w;q.push(v);//前缀异或和
t.insert_query(pre_xor[v]);//计算当前的最大的前缀异或和间的异或值
}
}
}
cout<<t.getans();
return 0;
}

小结

01字典树可以快速找到最大异或对。