关于卷积神经网络细节的深入理解
文章目录
Ⅰ.关于softmax,Cross-Entropy Loss,Hinge Loss,L2正则化基本概念的深入理解:
1.Softmax:
通常,我们希望获得所有类别标签的概率分布。 因此,我们通过Softmax函数将得分函数f的结果映射到介于0和1之间的区间。
2.Cross-Entropy Loss:
令(xi,yi)为一对训练样本,其中xi∈R^D为训练数据,yi∈RK为一个one-hot向量,除其真实类索引为1外,全零。 假设预测 y ^ i {\hat{y}}_i y^i∈RK是在Softmax之后计算的,则交叉熵损失为:
这里举个小例子:x输入为img,经过softmax之后得到不同的预测结果: y ^ i {\hat{y}}_i y^i和 y ^ i {\hat{y}}_i y^i的预测值分别为0.1,0.9;而这里的1,2分别代表猫和狗2个类别。那么此时的L1=-1•log(0.1),而L2=-1•log(0.9),L1>L2,所以这张图片更像狗而不是猫。理解:但是如果这张图片的标签是猫的话,我们就要不断训练前面的卷积层参数,使最终的预测分类更接近于猫。**
3.Hinge Loss:
注意,交叉熵损失的指数计算是相对复杂的,而有时我们不需要将预测结果映射到概率区间上。 因此,hinge Loss 的损失函数为:
j是其他类别的索引,yi是正确类别的索引。当f(xi-W)yi大于所有的f(xi,W)j+△时,损失值为0;这里的△是阈值,通过阈值判定分类正确与错误之间的界限。理解:Li含义是该输入的xi在其他类的得分大于正确分类的得分的累加作为损失值。
4.L2 norm:
正则化是防止模型学习过度拟合的常用技术。 最常见的正规化惩罚是L2范数,它通过对所有参数进行逐元素二次惩罚来阻止较大的权重:
k,d作为W权重矩阵的索引。
关于L2范数,以及正则化损失的理解:常见的范式表达形式,机器学习中 L1 和 L2 正则化的直观解释
由上可得final loss为:
总体的损失包括两项,即数据损失和正则化损失:
5.梯度的计算:
对于一个单独的数据点,hinge Loss如下:
我们可以区分权重的损失函数,取关于 w y i w_{y_i} wyi的梯度,我们得到:
对于j≠yi的其他行,梯度为:
【1()代表的是引导函数,条件成立时等于1,条件不成立时等于0。】
那么,Wj和Wyi在前向传播中是如何区分的呢?
这里展开举个例子,或许能够更好地去理解这里的概念:
假设我们有一个权重矩阵W∈R(K×D),偏差矢量b∈R(K×1),其中K是类别数,D是特征维数,然后给定输入xi∈R(D×1),得分函数f:RD→RK 是:
这里采用的是线性分类的概念,cat,dog和ship都有各自的权重模板以及独立的偏差。所以在实际的前向传播中,Wj和Wyi是可以区分并且单独计算出他们的梯度。
6.优化(OPtimization):
while True: (对于单独的data的训练,权重的优化)
weights_grad = gradient(loss_fun, data, weights)
weights += - step_size * weights_grad
理解:weights +=step_size * (-weights_grad)。step_size代表learning rate,-weights_grad的解释:沿着梯度下降最快的方向取反,这样使得下降的速度最慢,进行收敛的迭代计算;如果这里的取梯度的方向则收敛的速度最快。
而这里的中间层采用drop out去优化:
H1 = np.maximum(0, np.dot(W1, X) + b1) # forward pass
U1 = np.random.rand(H1.shape) < p # dropout mask
*H1 = U1 # drop
对于我们的最终目标是最小化总损失,让我们考虑hinge loss作为我们的目标函数。 如果我们将为“ true”标记的数据计算的分数称为s,将为“ false”标记的数据计算的分数称为sc。 那么优化目标是:
Trick(小技巧):把△固定为1,加速训练的收敛。
Ⅱ.反向传播(Backpropagation intution)的深入理解:
cost的变化∆C与权重的变化 Δ ω j k l \mathrm{\Delta}\omega_{j_k}^l Δωjkl的关系式如下:
而变化的 Δ ω j k l \mathrm{\Delta}\omega_{j_k}^l Δωjkl会在激活层中引起一个小的变化 Δ ω j l \mathrm{\Delta}\omega_{j}^l Δωjl:
那么如何理解这里的概念呢?
l代表第l层网络,j代表第l层的第j个神经元,k代表的是第k个分类类别的索引,这里的是线性模型,所以每个分类类别有自己的权重的索引。
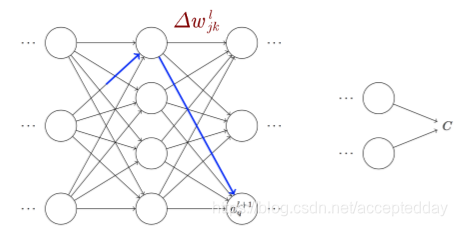
而∆C与权重的变化 Δ ω j k l \mathrm{\Delta}\omega_{j_k}^l Δωjkl之间的关系在网络中并非是直接关联起来的,而是通过中间无数层的卷积层。
激活量 Δ a j l \mathrm{\Delta}a_j^l Δajl的变化将导致下一层中所有激活的变化:
如果一条路径经过多个激活层 a j l , a q l + 1 . . . . . . a n L − 1 , a m L a_j^l,a_q^{l+1}......a_n^{L-1},a_m^L ajl,aql+1......anL−1,amL则结果表达式为:
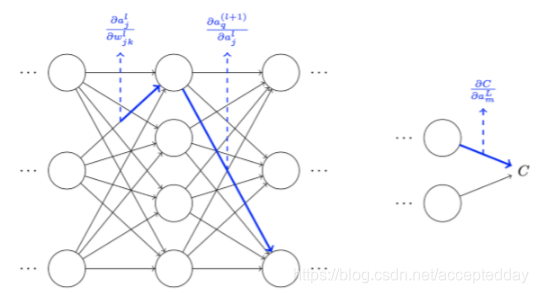
那么,把权重和成本之间的所有可能路径相加起来,便可以得到 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传 Δ ω j k l \mathrm{\Delta}\omega_{j_k}^l Δωjkl和ΔC之间的关系 :
而 ∂ w j k l , ∂ c \partial w_{jk}^l,\partial c ∂wjkl,∂c之间的关系是什么呢?由上式变形即可得到:
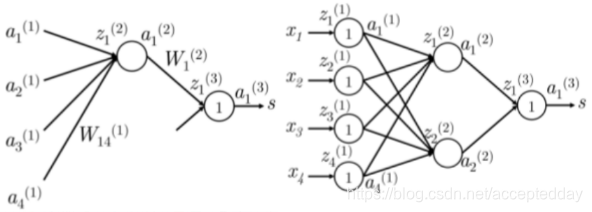
以 ∂ J ∂ w 14 ( 1 ) \frac{\partial J}{\partial w_{14}^{\left(1\right)}} ∂w14(1)∂J为例,我们来计算它的值是多少呢?
具体的计算过程如下:





 本文深入探讨了深度学习中关键的损失函数,如softmax、Cross-EntropyLoss、HingeLoss和L2正则化,详细解析了它们的计算原理及在反向传播中的应用,帮助读者理解模型优化背后的数学逻辑。
本文深入探讨了深度学习中关键的损失函数,如softmax、Cross-EntropyLoss、HingeLoss和L2正则化,详细解析了它们的计算原理及在反向传播中的应用,帮助读者理解模型优化背后的数学逻辑。
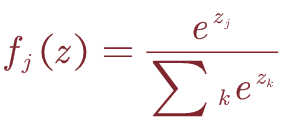
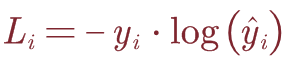
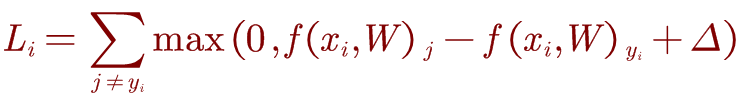
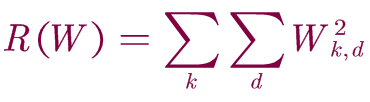
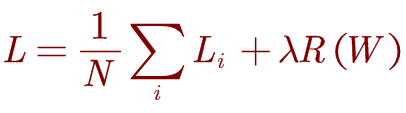
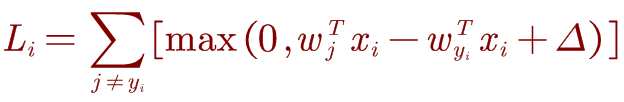
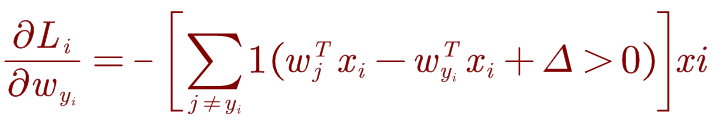



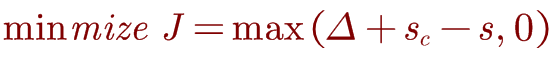
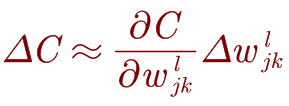
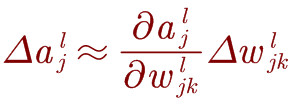
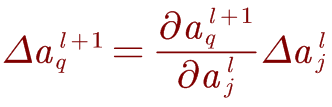

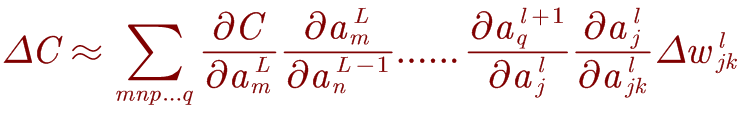
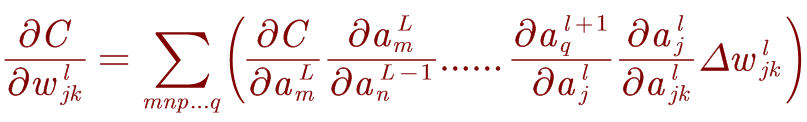
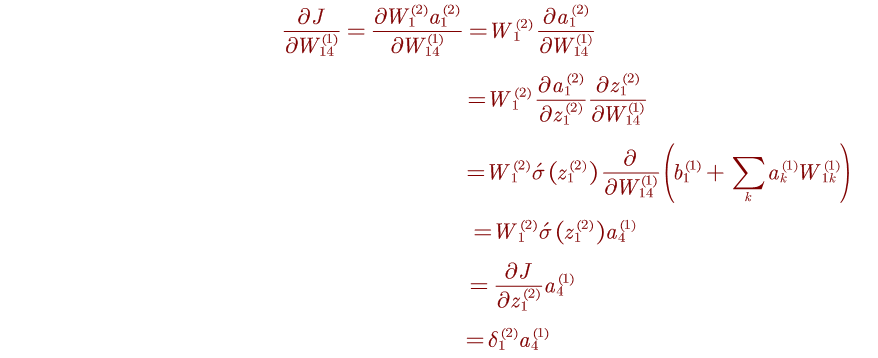


















 5997
5997

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










