【图 - 最短路径(Dijkstra & Frolyd)】

最短路径

最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。

从图中某一顶点(称为源点)到达另一顶点(称为终点)的路径可能不止一条，如何找到一条路径使得沿此路径上各边上的权值总和达到最小，例：公交查询系统。

问题解法：

求从某个源点到其余各点的最短路径 — Dijkstra算法

每一对顶点之间的最短路径 — Floyd算法

例如：

从某点到其他各顶点的最短路径

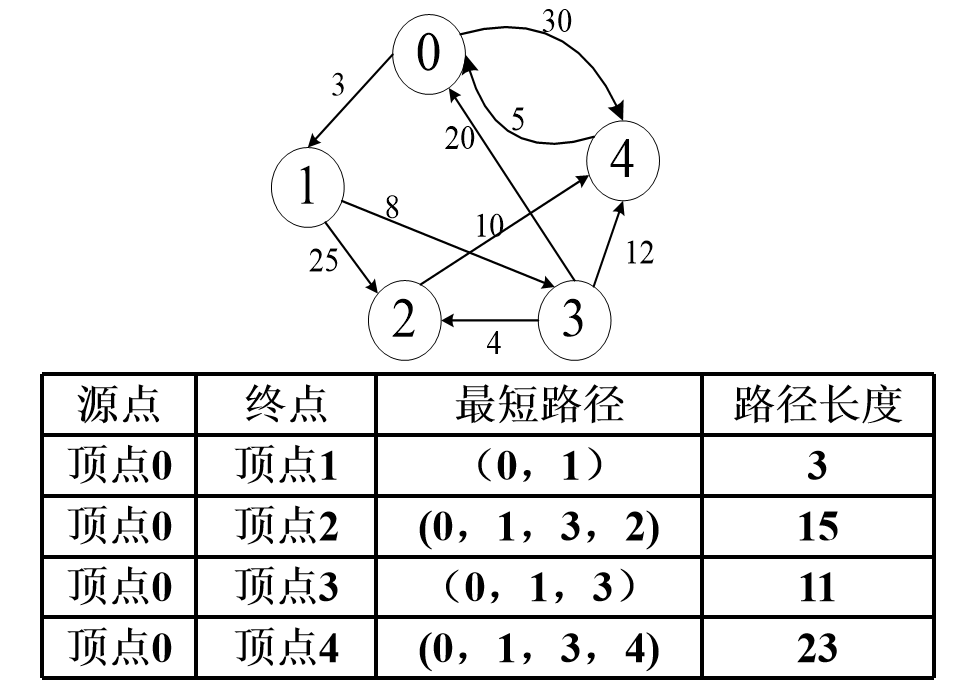
最短路径不一定是经过边最少的路径，但在这些最短路径中，长度最短的那一条路径上只有一条边，且它的权值在从源点出发的所有边的权值最小。

 路径长度最短的最短路径的特点：

在这条路径上，必定只含一条弧，并且这条弧的权值最小。

下一条路径长度次短的最短路径的特点：

它只可能有两种情况：或者是直接从源点到该点(只含一条弧)； 或者是从源点经过顶点v1，再到达该顶点(由两条弧组成)。 

迪杰斯特拉(Dijkstra)算法

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

设置辅助数组Dist，其中每个分量Dist[k]表示当前所求得的从源点到其余各顶点k的最短路径。

一般情况下，

Dist[k] = <源点到顶点k的弧上的权值> 或者 = <源点到其它顶点的路径长度>

+  <其它顶点到顶点k的弧上的权值>。

1）在所有从源点出发的弧中选取一条权值最小的弧，即为第一条最短路径。

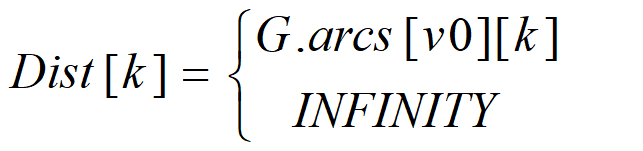
2）修改其它各顶点的Dist[k]值。 假设求得最短路径的顶点为u，