粒子群算法（固定权重和权值线性递减策略

粒子群算法

一、粒子群算法的概念

粒子群优化算法(PSO：Particle swarm optimization) 是一种进化计算技术（evolutionary computation）。源于对鸟群捕食的行为研究。粒子群优化算法的基本思想：是通过群体中个体之间的协作和信息共享来寻找最优解．
  PSO的优势：在于简单容易实现并且没有许多参数的调节。目前已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。

二、基本思想

粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。下面的动图很形象地展示了PSO算法的过程：

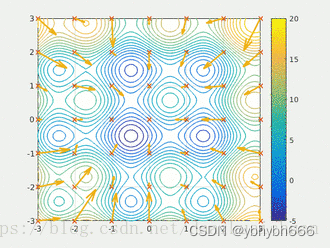
三、算法介绍

每个寻优的问题解都被想象成一只鸟，称为“粒子”，所有粒子都在一个D维空间进行搜索；
所有的粒子都由一个fitness function 确定适应值以判断目前位置的好坏；
每个粒子必须赋予记忆功能，能记住所搜寻到的最佳位置；
每一个粒子还有一个速度以决定飞行的距离和方向。这个速度根据它本身的飞行经验以及同伴的飞行经验进行动态调整。

如何更新位置呢?

PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次的迭代中，粒子通过跟踪两个“极值”(pbest，gbest)来更新自己。在找到这两个最优值后，粒子通过下面的公式来更新自己的速度和位置。

公式(1)的第一部分称为【记忆项】，表示上次速度大小和方向的影响；公式(1)的第二部分称为【自身认知项】，是从当前点指向粒子自身最好点的一个矢量，表示粒子的动作来源于自己经验的部分；公式(1)的第三部分称为【群体认知项】，是一个从当前点指向种群最好点的矢量，反映了粒子间的协同合作和知识共享。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。以上面两个公式为基础，形成了PSO的标准形式。

g为当前迭代次数
公式(2)和 公式(3)被视为标准PSO算法

算法流程图

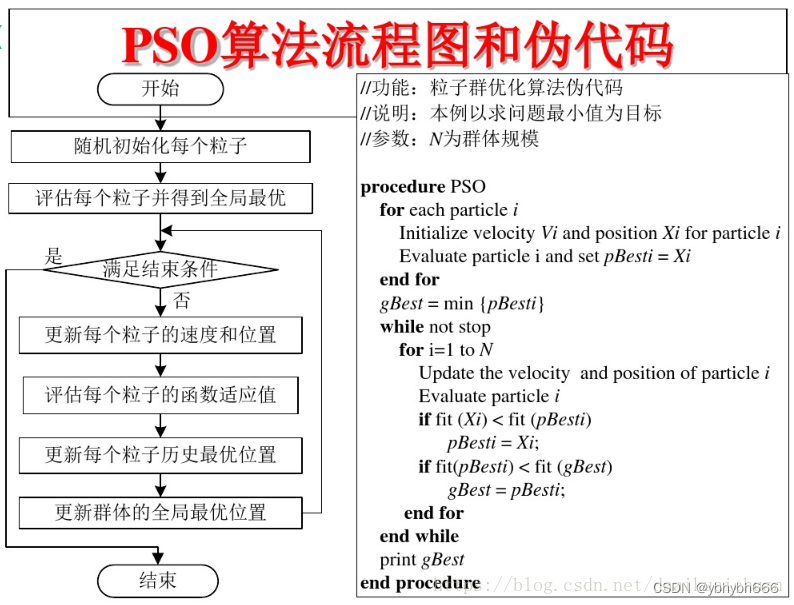
python 代码实现

一、权重是固定的，直接调用scikit-opt库即可

def demo_func(x):
	x1, x2, x3 = x
	return x1 ** 2 + (x2 - 0.05) ** 2 + x3 ** 2

from sko.PSO import PSO

pso = PSO(func=demo_func, n_dim=3, pop=40, max_iter=150, lb=[0, -1, 0.5], ub=[1, 1, 1], w=0.8, c1=0.5, c2=0.5)
pso.run()
print('best_x is ', pso.gbest_x, 'best_y is', pso.gbest_y)
import matplotlib.pyplot as plt

plt.plot(pso.gbest_y_hist)
plt.show()

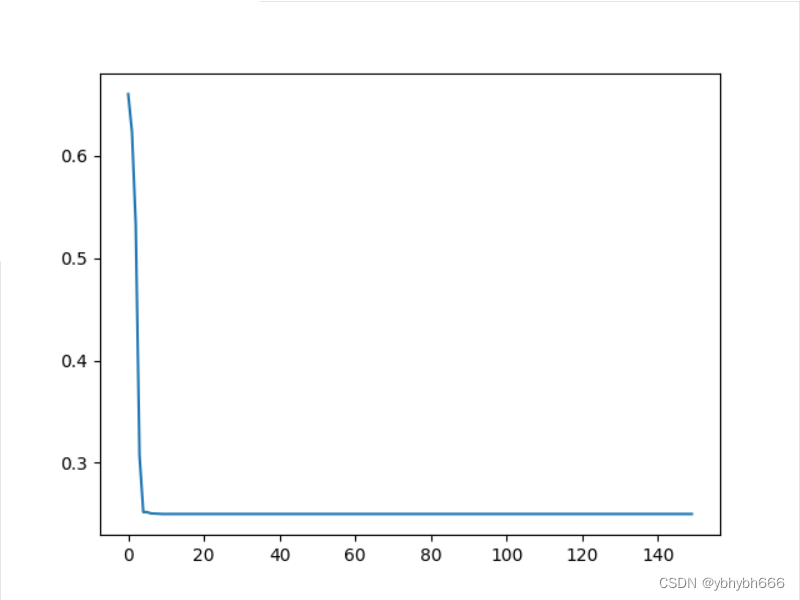
best_x is [0. 0.05 0.5 ] best_y is [0.25]

二、采用线性递减权值策略

import numpy as np
import matplotlib.pyplot as plt
import time

class PSO:
	def __init__(self, max_steps, max_size):

    	self.max_steps = max_steps  # 最大迭代次数
    	self.max_size = max_size  # 粒子数量
    	self.init_weight = self.cur_weight = 0.6  # 初始惯性权重与当前惯性权重
    	self.end_weight = 0.1
    	self.c1 = self.c2 = 2  # 个体学习因子、社会学习因子
    	self.boundary = [-10, 10]  # 粒子群取值范围（解空间范围）
    	self.dim = 2   # 维度
    	# 初始化粒子群位置
    	self.x = np.random.uniform(low=self.boundary[0],
        	                       high=self.boundary[1],
            	                   size=(max_size, self.dim)) # max_num行，2列
    	#	初始化粒子群速度
    	self.v = np.random.rand(self.max_size, self.dim)
    	# 计算当前所有粒子的适应值向量，所有粒子历史最佳适应度及其对应位置
    	self.curFitness = self.get_fitness(self.x)
    	self.individualBestFitness = self.curFitness
    	self.pbest = self.x
    	# 获取全局最佳适应度及其最佳位置
    	self.globalBestFitness = np.min(self.individualBestFitness)
    	self.gbest = self.x[np.argmin(self.individualBestFitness)] # np.argmin 给出水平方向最小值的下标

	def get_fitness(self, x):
    	# 按行求平方和，即 X^2 + Y^2
    	return np.sum(np.square(x), axis=1)

	def evolve(self):
    	self.iter = 0
    	for step in range(self.max_steps):
        	self.iter = self.iter + 1
        	self.cur_weight = (self.init_weight - self.end_weight) * float(self.max_steps - 	self.iter) / float(self.max_steps) + self.end_weight
        	# 生成两个随机数，分别代表飞向当前粒子历史最佳位置、全局历史最佳位置的程度
        	r1 = np.random.rand(self.max_size, self.dim)
        	r2 = np.random.rand(self.max_size, self.dim)
        	# 更新速度和权重
        	self.v = self.cur_weight * self.v + self.c1 * r1 * (self.pbest - self.x) \
            	     + self.c2 * r2 * (self.gbest - self.x)
        	self.x = self.x + self.v

        	# 画图
        	plt.clf()  # 清除当前 figure, 不关闭窗口
        	plt.scatter(self.x[:, 0], self.x[:, 1], s=30, color='r')  # s代表大小，k代表black
        	# x、y轴作图范围
        	plt.xlim(self.boundary[0], self.boundary[1])
        	plt.ylim(self.boundary[0], self.boundary[1])
        	# 画面停顿，以秒为单位
        	plt.pause(0.01)

        # 计算当前所有粒子的适应值向量，所有粒子历史最佳适应度及其对应位置
        self.curFitness = self.get_fitness(self.x)
        update_id = np.greater(self.curFitness, self.individualBestFitness)
        self.individualBestFitness[update_id] = self.curFitness[update_id]
        self.pbest[update_id] = self.x[update_id]
        # 获取全局最佳适应度及其最佳位置
        if self.globalBestFitness > np.min(self.individualBestFitness):
            self.globalBestFitness = np.min(self.individualBestFitness)
            self.gbest = self.x[np.argmin(self.individualBestFitness)]
        # 增加一个终止条件，以便计算寻找到最优值的耗时与迭代次数
        if self.globalBestFitness - 0.0 < 1e-10:
            break
        print('global best fitness: %.5f, current mean fitness: %.5f' % (self.globalBestFitness, np.mean(self.curFitness)), end=" ")
        print("最优位置：", self.gbest)

if __name__ == "__main__":

	pso = PSO(100, 100)
	start = time.time()
	pso.evolve()
	print("寻找到近似最优解时，共迭代了", pso.iter, "次,总共耗费了", (time.time() - start), "秒")
	plt.show()

…
…
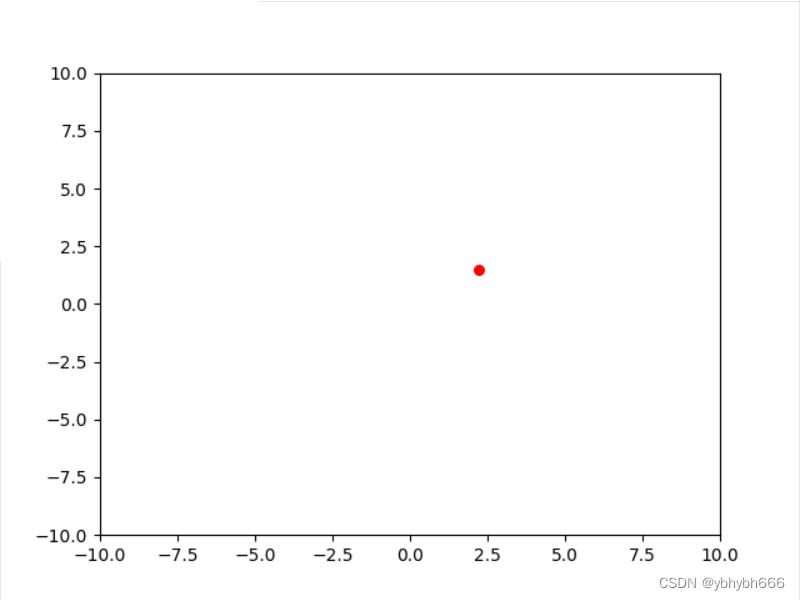
global best fitness: 0.79342, current mean fitness: 3720866650.27552 最优位置： [2.20486796 1.46367231]
global best fitness: 0.79342, current mean fitness: 12798048910.50933 最优位置： [2.20486796 1.46367231]
global best fitness: 0.79342, current mean fitness: 45255640371.19971 最优位置： [2.20486796 1.46367231]
global best fitness: 0.79342, current mean fitness: 13514831135.52687 最优位置： [2.20486796 1.46367231]
global best fitness: 0.79342, current mean fitness: 81197345712.78462 最优位置： [2.20486796 1.46367231]
寻找到近似最优解时，共迭代了 100 次,总共耗费了 18.308581829071045 秒