一、实验目的(本次实验所涉及并要求掌握的知识点)
掌握初等模型的建模方法,对简单的初等模型能借助Matlab工具软件进行辅助建模和求解。
二、实验内容与设计思想(设计思路、主要数据结构、主要代码结构、主要代码段分析、电路图)
1. 曲线最小二乘拟合问题:
- 多项式拟合(线性最小二乘拟合):
1. 设计思路
- 首先定义了两个数组 x 和 y,分别表示自变量和因变量的取值。
- 使用 polyfit 函数进行二次多项式拟合,得到拟合的系数。
- 打印出拟合的二次多项式的系数。
- 生成更细致的 x 值,用于绘制拟合曲线,通过 polyval 计算对应的 y 值。
- 使用散点图和折线图将原始数据和拟合曲线绘制出来。
2. 主要数据结构
- x:自变量的值。
- y:因变量的值。
- p:存储拟合后得到的二次多项式系数。
3. 主要代码结构
- 用 polyfit 函数进行拟合。
- 用 fprintf 输出拟合系数。
- 用 linspace 和 polyval 生成拟合曲线的数据点。
4. 主要代码段分析
- p = polyfit(x, y, 2);
分析:用于计算 x 和 y 的二次多项式系数。返回一个包含多项式系数的数组 p,其中 p(1) 是二次项系数,p(2) 是一次项系数,p(3) 是常数项。
- scatter(x, y, 'filled');
- hold on;
- plot(x1, y1, 'LineWidth', 2);
分析:创建新的图形窗口,绘制原始数据点和拟合曲线,使用不同的图形元素进行区分。
- 运行结果图
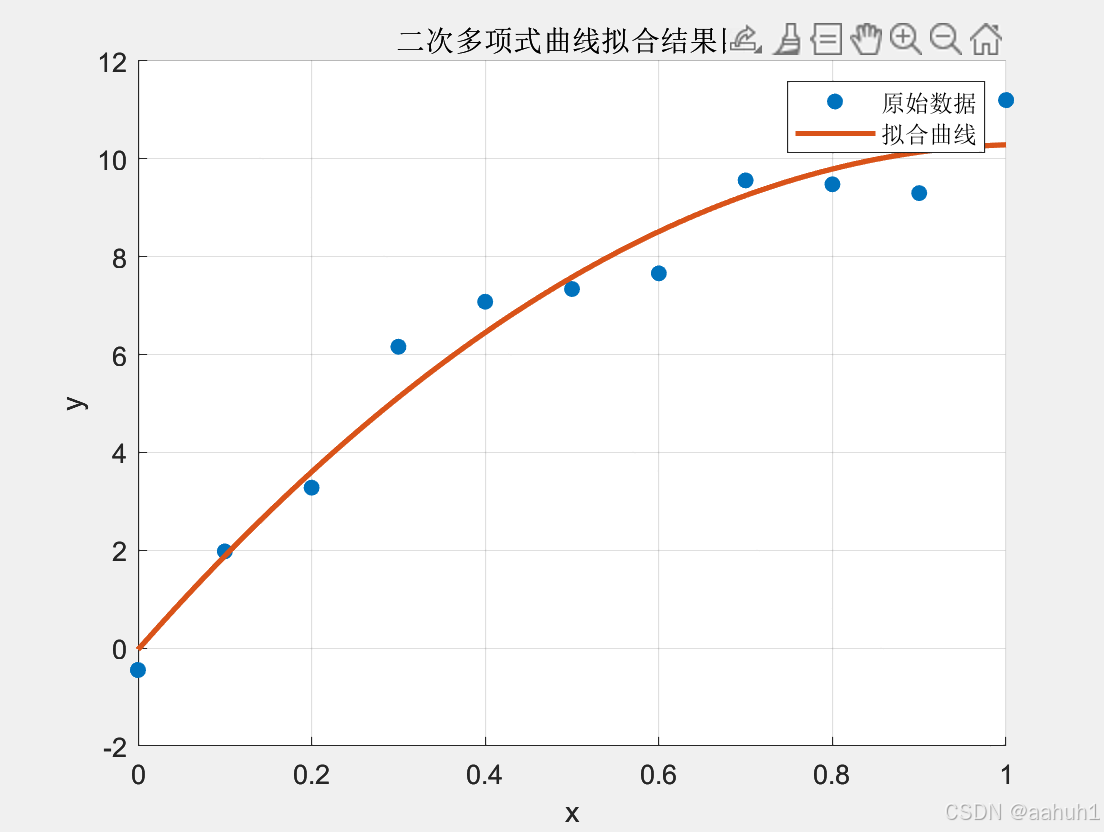
图 1 二次多项式曲线拟合结果图
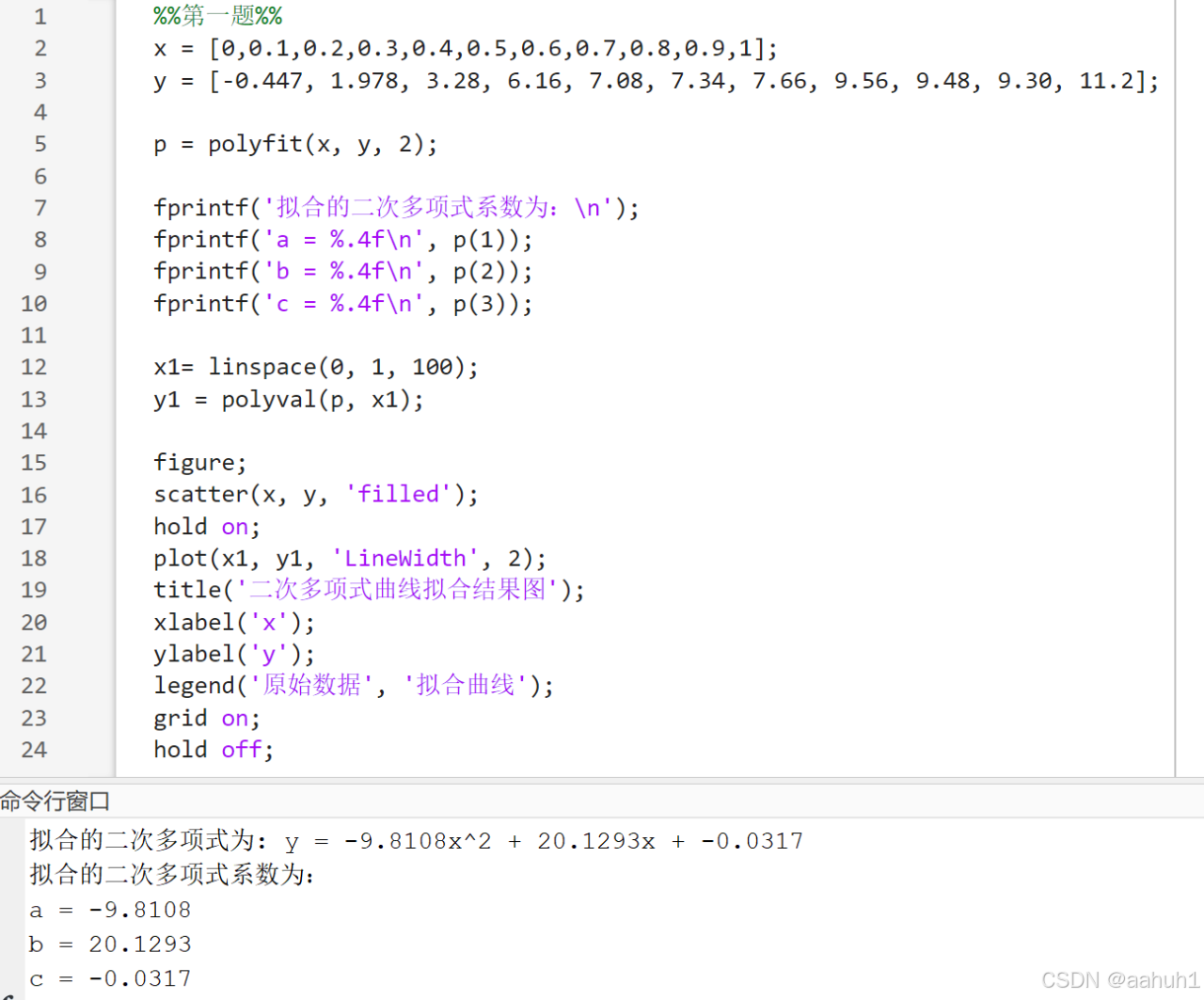
图 2 线性最小二乘拟合代码
- 非线性曲线拟合:
Lsqcurvefit函数:
1. 设计思路
- 定义了两个数组 t 和 y,分别表示自变量和因变量的取值。
- 使用匿名函数 modelFunc 定义了一个指数衰减模型,该模型依赖于参数A和输入变量 t。
- 设定拟合参数的初始猜测值 A0。
- 使用 lsqcurvefit 函数对模型进行拟合,并计算最佳参数。
- 打印出拟合得到的参数值。
2. 主要数据结构
- t:存储自变量。
- y:存储因变量。
- A0:初始猜测参数的数组。
3. 主要代码结构
拟合过程:调用 lsqcurvefit 进行模型拟合。
4. 主要代码段分析
- modelFunc = @(A, t) A(1) + A(2) * exp(-0.02 * A(3) * t);
分析:定义了一个匿名函数 modelFunc,用于表示拟合模型。该模型形式是一个常数项加上一个指数衰减项,依赖于参数 A 和输入变量 t。
- options = optimset('Display', 'off');
- [A1, resnorm] = lsqcurvefit(modelFunc, A0, t, y, [], [], options);
分析:使用 lsqcurvefit 函数进行非线性最小二乘拟合。modelFunc 是待拟合的模型,A0 是初始猜测,t 和 y 是数据,options 用于控制输出信息。返回值 A1 是拟合得到的参数,resnorm 是残差平方和。
- 运行结果图
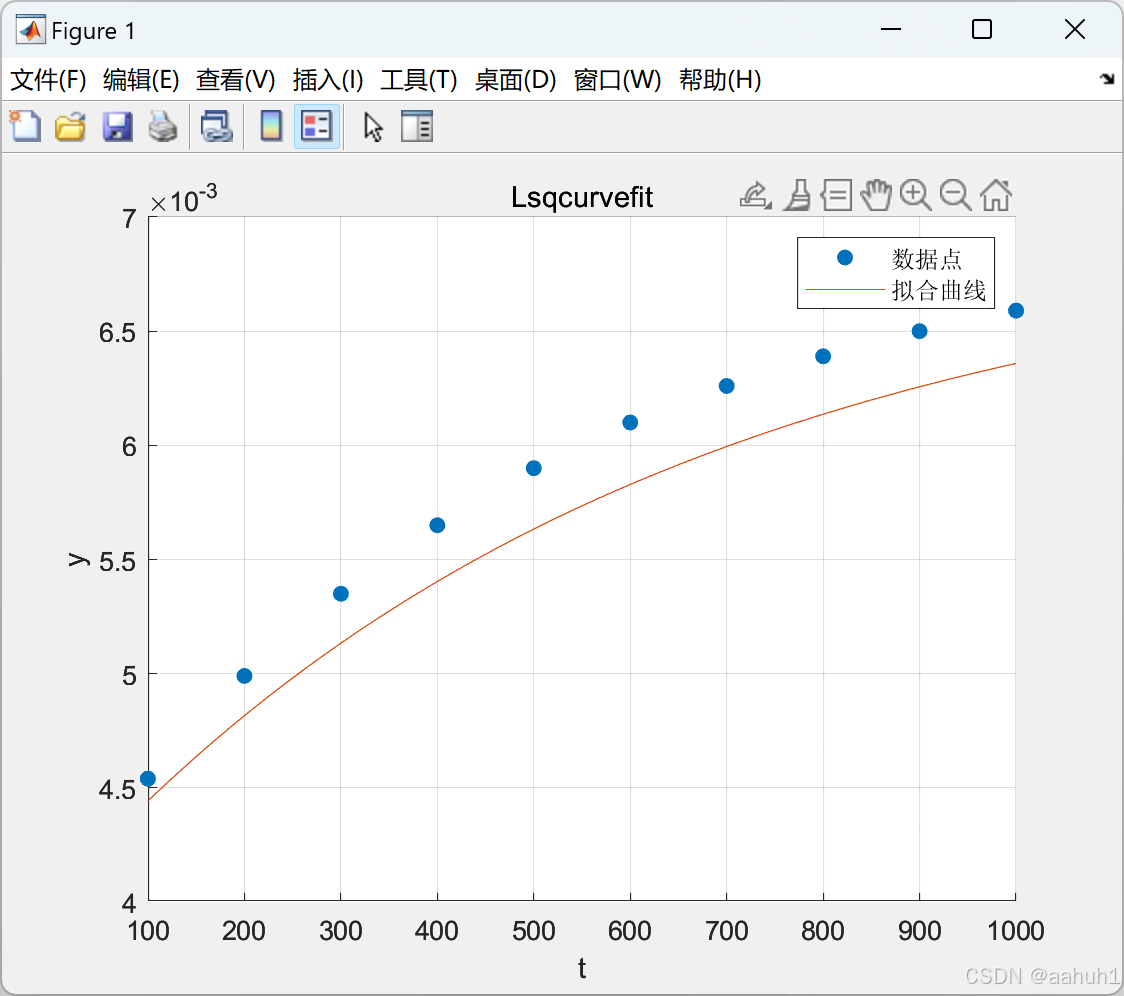
图 3 Lsqcurvefit函数
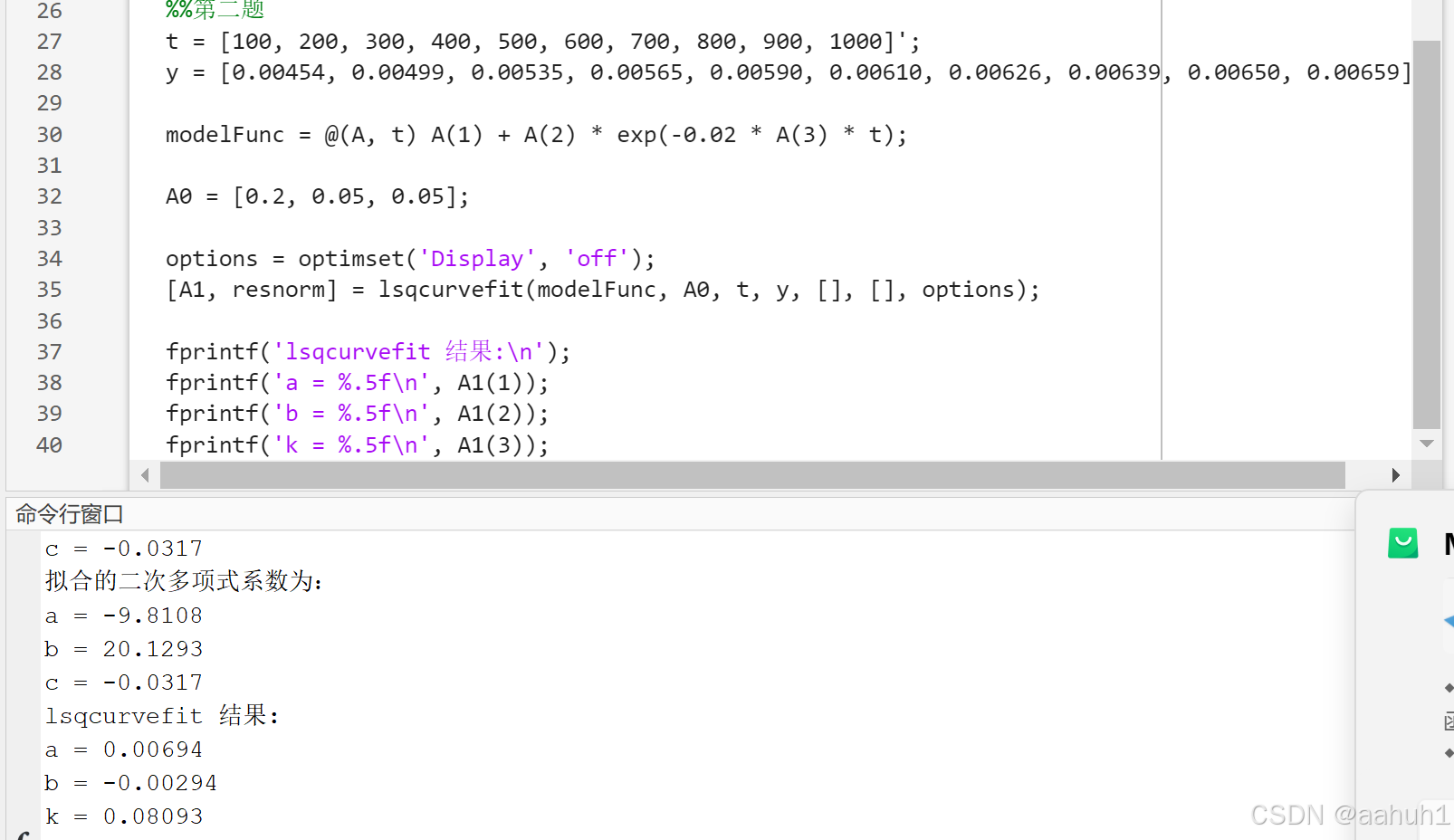
图 4 用Lsqcurvefit函数非线性拟合
Lsqnonlin函数:
1. 设计思路
利用非线性最小二乘法 (lsqnonlin) 拟合模型参数,使模型输出与实际数据之间的残差最小化。
2. 主要数据结构
- t:自变量。
- y:因变量。
- A0:初始参数猜测,包含三个参数的列向量。
3. 主要代码结构
- 定义 t 和 y。
- 计算模型预测与实际值之间的差异。
- 给出参数的初始猜测。
- 使用 lsqnonlin 进行参数优化。
- 打印拟合得到的参数值。
4. 主要代码段分析
- residualsFunc = @(A) modelFunc(A, t) - y;
分析:匿名函数用于计算模型预测与实际值的残差。
- options = optimoptions('lsqnonlin', 'Display', 'off');
- [A_fit_nonlinear, resnorm_nonlinear] = lsqnonlin(residualsFunc, A0, [], [], options);
分析:使用 lsqnonlin 进行拟合,返回最佳参数和残差平方和。
- 运行结果图
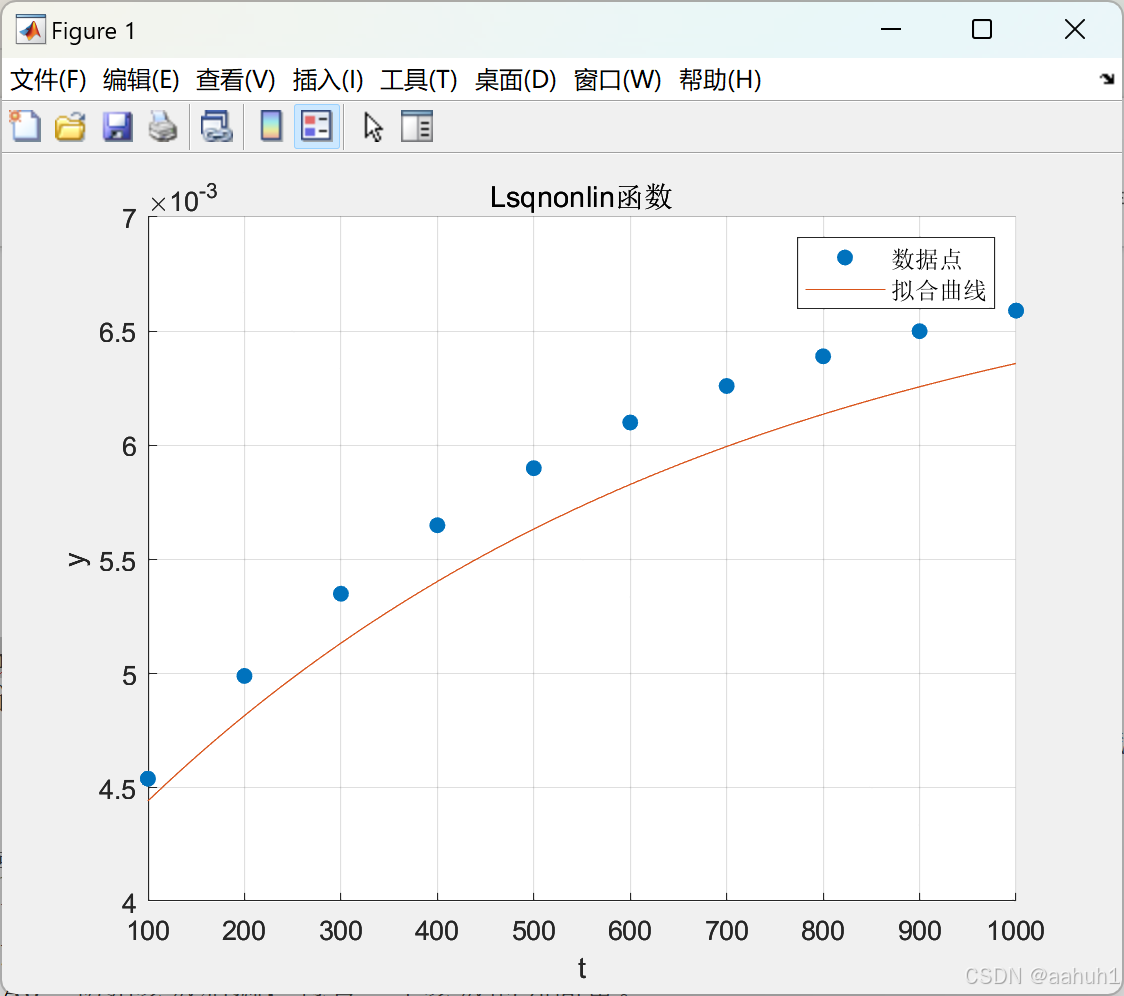
图 5 Lsqnonlin函数
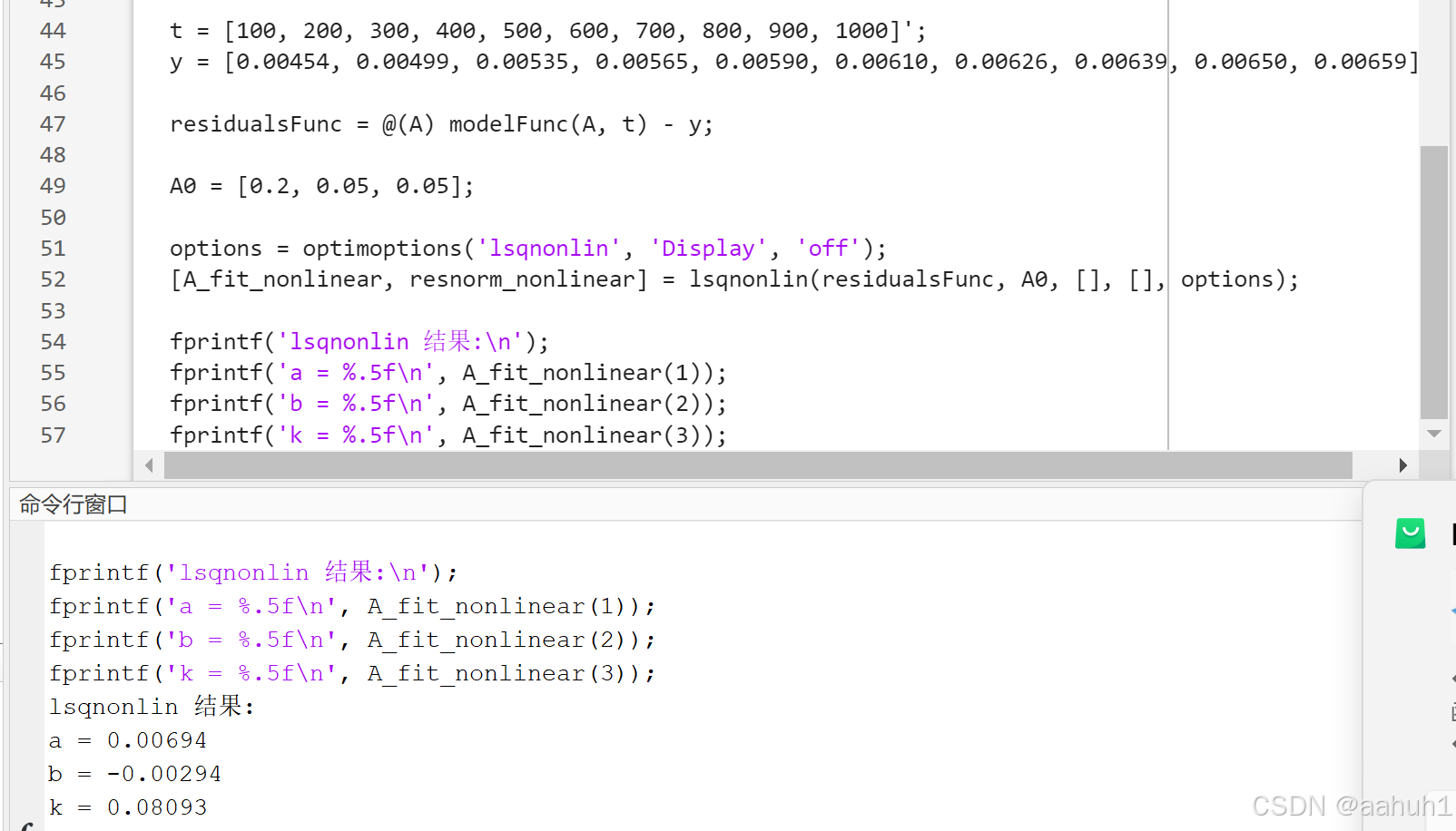
图 6 用Lsqnonlin函数非线性拟合
2. 初等模型求解:
1) 汽车刹车距离模型
- 设计思路:利用物理公式来计算不同初速度下的刹车距离。
2. 主要数据结构
- v0:初速度的数组。
- s:刹车距离的数组,初始化为零。
3. 主要代码结构
- 定义初速度 v0 和加速度 a。
- 使用物理公式计算每个初速度对应的刹车距离。
- 打印初速度与刹车距离的表格。
- 绘制初速度与刹车距离的关系图。
4. 主要代码段分析
- s = (v0.^2) / (2 * a);
分析:使用公式进行向量运算,快速计算所有初速度对应的刹车距离。
- 运行结果图
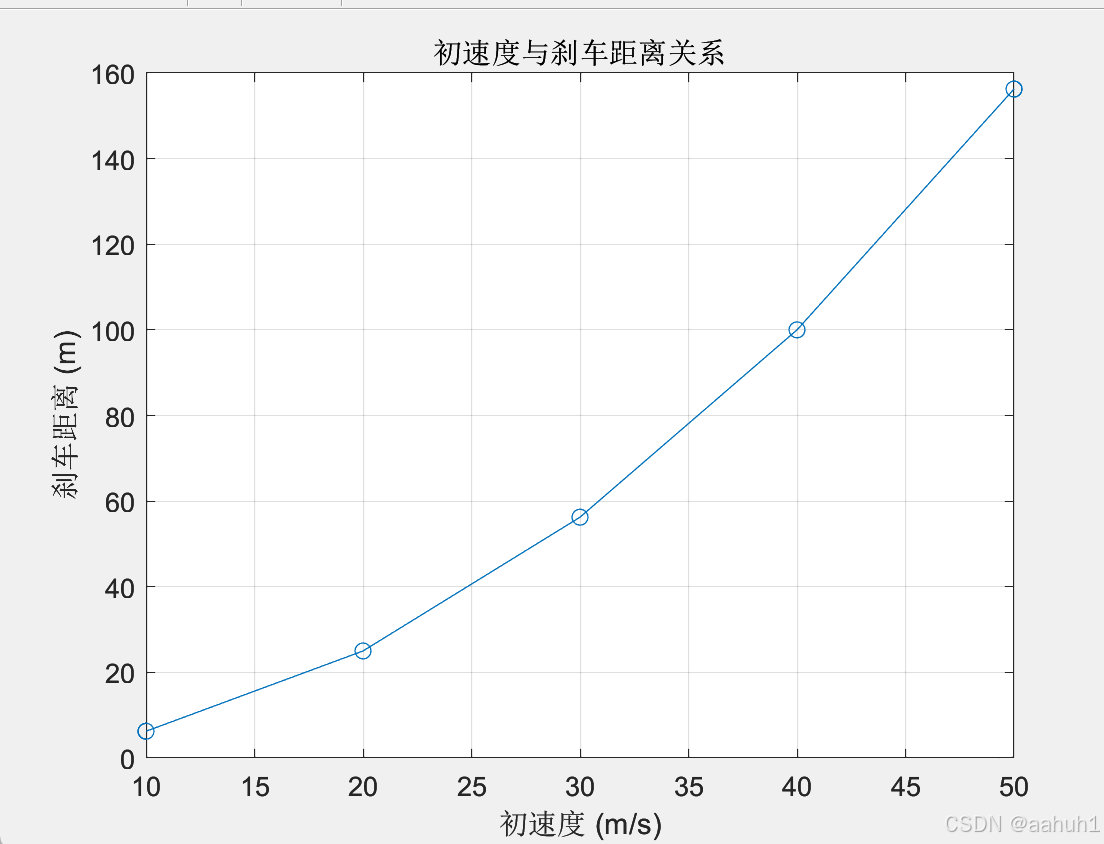
图 7 初速度与刹车距离关系
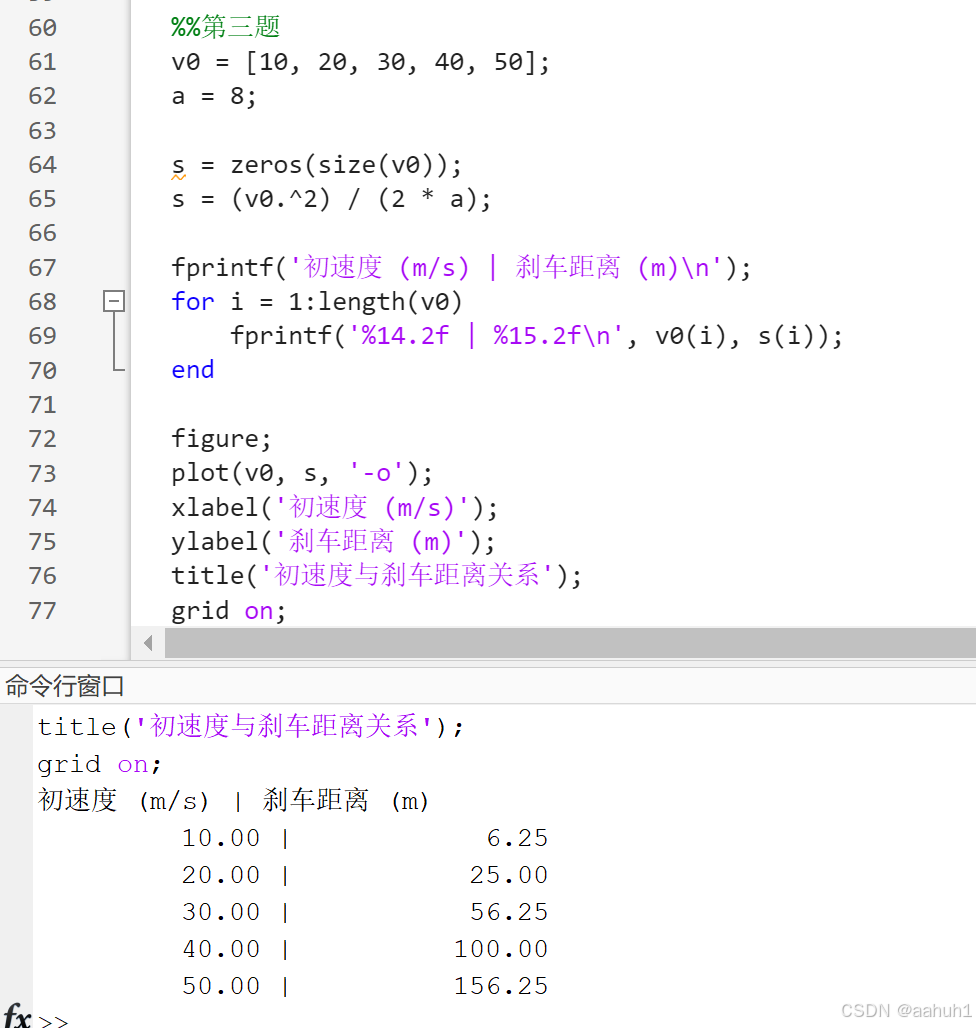
图 8 初速度与刹车关系运行结果
2. 举重关系模型
- 设计思路
通过对举重运动员的级别和成绩数据进行对数变换,使用线性回归拟合幂函数模型,从而预测不同重量级别下的成绩,并比较拟合模型与指定模型的预测值,同时计算并排名2020年东京奥运会的折合成绩。
2. 主要数据结构
- weights_world:各级别的重量(kg)。
- records_world:对应的总成绩(kg)。
- log_weights、log_records:对数变换后的数据。
- predicted_fit、predicted_specified:拟合模型和指定模型的预测值。
- weights_olympics、records_olympics:东京奥运会的数据。
- ranked_scores、rank_indices:排序后的折合成绩及其索引。
3. 主要代码结构
- 定义世界级别的重量和成绩。
- 将重量和成绩进行对数变换以便于线性回归。
- 使用polyfit函数对对数变换后的数据进行一次多项式拟合,计算出模型参数。
- 分别计算拟合模型和指定模型的预测值。
- 输出实际成绩与预测成绩的比较。
- 计算2020年东京奥运会的折合成绩并进行排名。
4. 主要代码段分析
coeffs = polyfit(log_weights, log_records, 1);
b = coeffs(1); % 斜率
log_a = coeffs(2); % 截距
a = exp(log_a); % 计算 a
分析:使用线性回归得到拟合的幂函数模型的参数,其中b是斜率,a是经过指数变换后的截距。
equivalent_scores = a * (weights_olympics .^ b);
[ranked_scores, rank_indices] = sort(equivalent_scores, 'descend');
分析:根据拟合模型计算奥运会各级别的折合成绩,并进行降序排序。
- 运行结果图
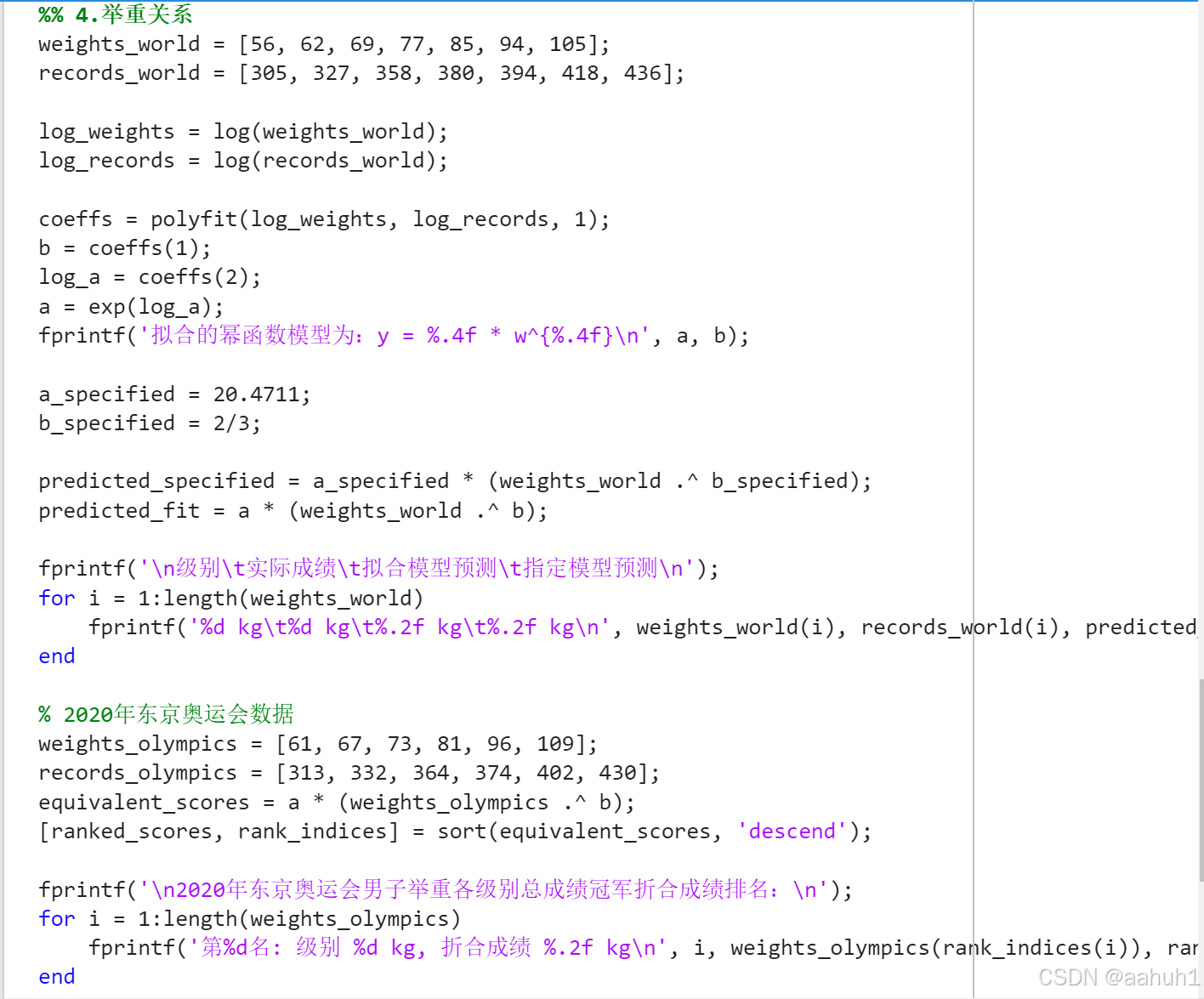
图 9 总代码1

图 10 总代码2
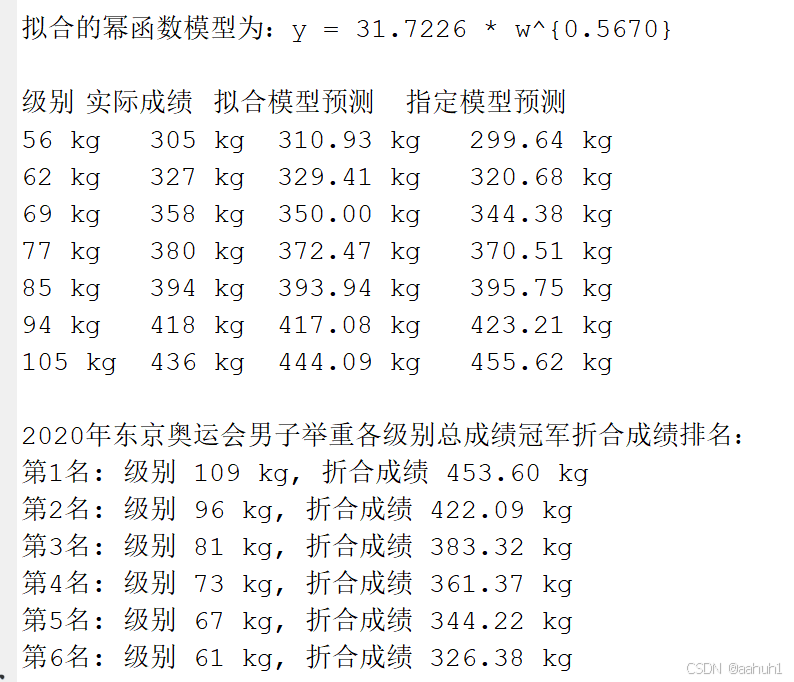
图 11 运行结果图
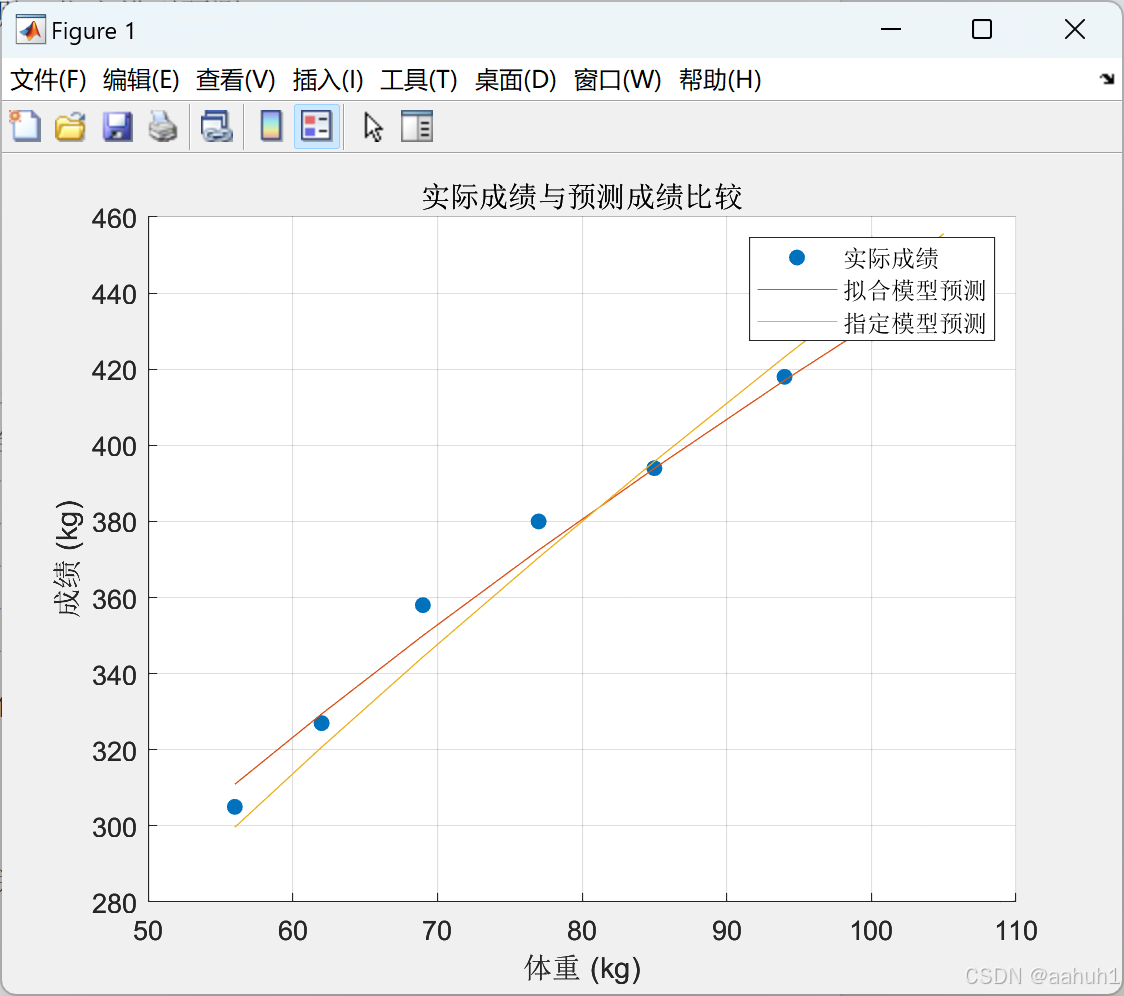
图 12 实际成绩与预测成绩比较图
三、实验使用环境(本次实验所使用的平台和相关软件)
MATLAB
四、实验步骤和调试过程(实验步骤、测试数据设计、测试结果分析)
1. 实验步骤
- 对于实验二的每一题都是先定义题中的自变量和因变量,以便进行后续分析。
- 前两题进行线性拟合与非线性拟合,刹车问题利用物理公式计算出未知数,而最后一题是先对重量和成绩进行对数变换,使其符合线性关系,后使用polyfit函数对对数变换后的数据进行一次多项式拟合,计算出幂函数模型的参数(斜率和截距)。
- 打印拟合的模型公式,展示模型的形式及参数。
- 制作直观图或带入问题计算。
2. 测试数据设计
1)多项式拟合:
自变量 x:包含10个数据点。
因变量 y:与 x 对应的一组观察值,展示非线性关系。
2)刹车问题:
初速度 v0:设置为 10, 20, 30, 40, 50 m/s,测试不同速度下的刹车效果。
加速度 a:固定为 8 m/s²,以模拟特定制动条件。
3)体重问题:
- 世界级别数据:
重量(kg):[56, 62, 69, 77, 85, 94, 105]
成绩(kg):[305, 327, 358, 380, 394, 418, 436]
这些数据用于建立基本的幂函数模型,反映不同级别运动员的表现。
- 2020年东京奥运会数据:
重量(kg):[61, 67, 73, 81, 96, 109]
成绩(kg):[313, 332, 364, 374, 402, 430]
这些数据用于评估在实际赛事中运动员的表现,并计算出折合成绩以便进行排名。
3. 测试结果分析
1)多项式拟合:
- 输出的二次多项式系数提供了函数的具体形式。
- 散点图与拟合曲线的结合展示了拟合效果,便于判断模型的拟合程度。图中显示了数据点和拟合曲线的吻合程度。
2)刹车问题:
曲线图显示刹车距离随初速度平方增长,反映出较高速度下刹车需求增加。
3)举重问题:
- 拟合模型参数:
通过线性回归得到的幂函数模型形式为 y = a * w^b,其中a和b是通过数据拟合得到的参数。打印出的模型可以用于预测其他级别的成绩。
- 预测值比较:
将实际成绩与拟合模型和指定模型的预测值进行比较,以评估模型的准确性。通过输出的表格,可以直观地观察到哪个模型更接近实际成绩。
五、实验小结(实验中遇到的问题及解决过程、实验中产生的错误及原因分析、实验体会和收获)
- 这次实验使我明白了在任何数据分析中,确保数据的准确性和完整性是基础。只有验证数据才能保证后续分析的有效性。
- 我初步掌握了初等模型的建模方法,对简单的初等模型能借助Matlab工具软件进行辅助建模和求解。
- 本次实验暴露出来的最大的问题还是和实验一一样,对于基础函数的了解不够深刻,在每一题都需要重新上网搜索,了解新函数的用法。
- 在实验中,我对于浮点数和整数的格式使用不当,导致输出结果混乱。而后我检查每个 fprintf 的调用,确保格式字符串与传入参数的类型一致。并且使用 %f 替代 %d 处理浮点数,确保输出的可读性。




















 1146
1146

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








