机器学习读书笔记----决策树

原创于 2018-10-12 15:49:42 发布 · 400 阅读

·

0

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

机器学习（周志华）学习笔记专栏收录该内容

4 篇文章

订阅专栏

基本介绍

决策树是一类常见的机器学习方法。

举个简单的例子，我们分辨一个艺术品是否具有艺术价值，可以从色彩，线条两方面去评价（不会美术，只是打个比方）。

例如下面这幅画，我们可以先判断色彩不鲜艳，再判断线条不美观，从而得出这没有艺术价值。

这判断的过程就是一棵决策树。如图

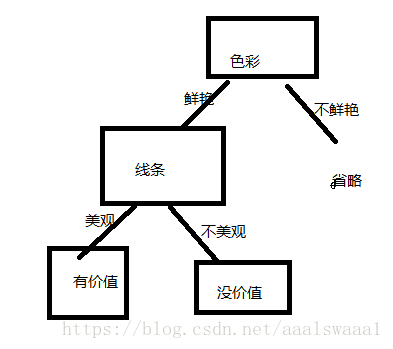
这是决策树学习基本算法

可以看出，关键在第8行，我们要如何选取最优的划分属性呢，从上例来说为什么要先看色彩而不是先看线条呢，当训练数据有一定量的时候，比如很多幅画，那么我们希望随着划分过程的不断进行，在分支结点所包含的样本尽可能来自同一类别，即结点的纯度越来越高。信息熵就是度量样本集合纯度最常用的一种指标。

划分选择

信息熵

$Ent(D)=-\sum^{|y|}_{k=1}p_klog_2(p_k)$

其中，D是数据集，y是类别数，p是在D中第k类样本所占的比例。

显然，信息熵的值越小，D的纯度越高。

信息增益
$Gain(D,a)=Ent(D)-\sum^{V}_{v=1}\frac{|D^v|}{|D|}Ent(D^v)$

假定离散属性a有v个取值，如色彩（鲜艳，暗淡，平淡），就有3个，Dv是第v个分支结点包含了D中所有在a上取值为 $a^v$ 的样本。

一般来说，信息增益越大，则说明使用该属性划分所获得的纯度提升越大。ID3就使用这个来划分。

实际上，信息增益准则对可取值数目较多的属性有所偏好。

增益率

为了减少信息增益的偏好的不利影响，也可以用增益率来作为划分标准。

$Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}$

其中

$IV(a)=-\sum^V_{v=1}\frac{|D^v|}{|D|}log_2\frac{|D^v|}{|D|}$

需要注意的是，增益率准则对可取值数目较少的属性有所偏好，因此在C4.5中是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

基尼指数

CART决策树使用基尼指数来选择划分属性。

数据集D的纯度可以用基尼值来表示，直观地说，Gini（D）反映了从数据集D中随机取两个样本其类别标记不一致的概率，因此Gini（D）越小，数据集D的纯度越高。

$Gini(D)=\sum^{|y|}_{k=1}\sum_{k^{'}\neq k}p_kp_{k^'}}$

$=1-\sum^{|y|}_{k=1}p^2_k$

属性a的基尼指数为

$Gini\_index(D,a)=\sum^{V}_{v=1}\frac{|D^v|}{|D|}Gini(D^v)$

代码实现

https://blog.youkuaiyun.com/aaalswaaa1/article/details/83005728

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。