上一节呢,我们初探了《概率与数理统计》,这次我们续接上一节的内容,来专题学习《条件概率、全概率、贝叶斯公式》
注! 声明,本文转载,本文转载,本文转载!
本文转载,侵删! 感谢博主”hearthougan”(✈机票点我)
一、条件概率公式
举个例子,比如让你背对着一个人,让你猜猜背后这个人是女孩的概率是多少?直接猜测,肯定是只有50%的概率,假如现在告诉你背后这个人是个长头发,那么女的概率就变为90%。所以条件概率的意义就是,当给定条件发生变化后,会导致事件发生的可能性发生变化。
条件概率由文氏图出发,比较容易理解:
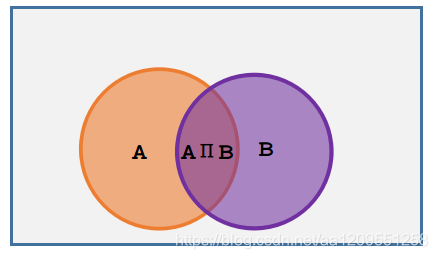
p ( A ∣ B ) p(A|B) p(A∣B)表示B发生后A发生的概率,由上图可以看出B发生后,A再发生的概率就是 P ( A ∩ B ) P ( B ) \frac{P(A\cap B)}{P(B)} P(B)P(A∩B),
因此: p ( A ∣ B ) = P ( A ∩ B ) P ( B ) p(A|B) = \frac{P(A\cap B)}{P(B)} p(A∣B)=P(B)P(A∩B)
由:
p ( A ∣ B ) = P ( A ∩ B ) P ( B ) ⇒ p ( A ∩ B ) = p ( A ∣ B ) × p ( B ) p(A|B) = \frac{P(A\cap B)}{P(B)}\Rightarrow p(A\cap B) = p(A|B) \times p(B) p(A∣B)=P(B)P(A∩B)⇒p(A∩B)=p(A∣B)×p(B)
⇒ p ( A ∩ B ) = P ( B ∣ A ) × P ( A ) \Rightarrow p(A\cap B) = P(B|A) \times P(A) ⇒p(A∩B)=P(B∣A)×P(A)
得:
p ( A ∣ B ) = P ( A ∩ B ) P ( B ) = p ( B ∣ A ) × P ( A ) p ( B ) p(A|B) = \frac{P(A\cap B)}{P(B)}=\frac{p(B|A) \times P(A)}{p(B)} p(A∣B)=P(B)P(A∩B)=p(B)p(B∣A)×P(A)
这就是条件概率公式。
假如事件A与B相互独立,那么:
p ( A ∩ B ) = P ( A ) × P ( B ) p(A\cap B)=P(A) \times P(B) p(A∩B)=P(A)×P








 本文介绍了条件概率、全概率和贝叶斯公式,通过实例详细阐述了这三个概念。条件概率是给定条件变化后事件发生的可能性;全概率公式用于计算通过多种途径达到某一目标的概率;贝叶斯公式则是在已知结果的情况下,求导致该结果的原因概率。
本文介绍了条件概率、全概率和贝叶斯公式,通过实例详细阐述了这三个概念。条件概率是给定条件变化后事件发生的可能性;全概率公式用于计算通过多种途径达到某一目标的概率;贝叶斯公式则是在已知结果的情况下,求导致该结果的原因概率。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








