[Uva P11168] Airport

最新推荐文章于 2025-10-29 21:13:13 发布

转载最新推荐文章于 2025-10-29 21:13:13 发布 · 141 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/whc200305/p/7076766.html

本文探讨了一种寻找平面上n个点到某直线平均距离最小的解决方案，通过构建点集的凸包并枚举其边，利用直线方程计算平均距离，最终找到最优直线。

题目是英文的，这里就不给出来了。

题目的大意是说，在平面上有n个点，要找一条直线，使所有点到直线的平均距离最小，且这些点都在该直线的同一侧（包括直线上）。

那么，既然要使距离最小化，还要使所有点一定在这条直线的同一侧或在这条直线上。恰好，所有点构成的凸包的每条边所在直线都满足了这一要求，并且，凸包上的边比凸包外

边更优。

那么，我们完全可以现将凸包上的点算出（这次用了快而稳的Andrew），然后枚举相邻两点构成的直线。那么，问题来了——平均距离怎么求？如下：

我们已知直线的两个点：(x1,y1),(x2,y2)，也就知道了直线的两点式：

(x1-x)/(x1-x2)=(y1-y)/(y1-y2)，整理一下：

x1y1-x1y2-xy1+xy2=x1y1-x1y-x2y1+x2y

(y2-y1)x+(x1-x2)y+(x2y1-x1y2)=0（也就是一般式Ax+By+C=0）

其中A=y2-y1,B=x1-x2,C=x2y1-x1y2。

这有什么用？

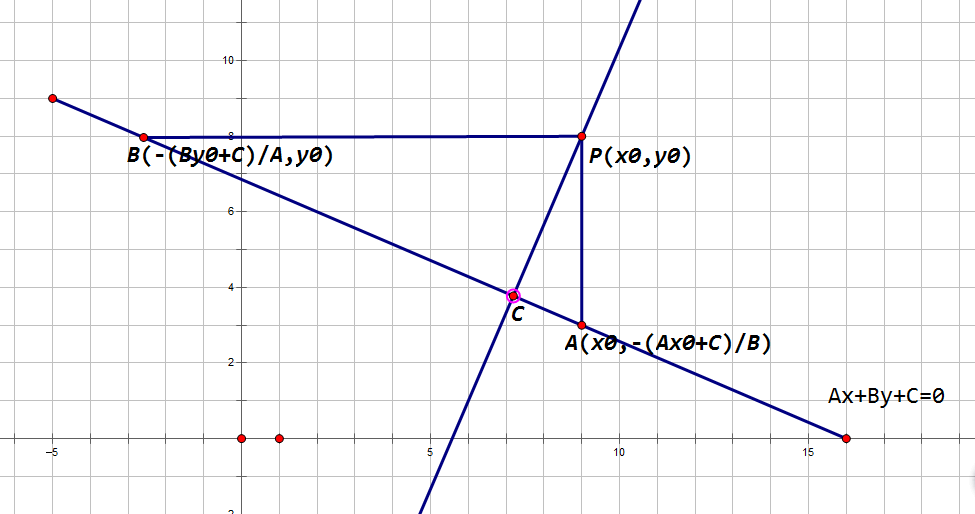
如图，AP*BP=AB*CP，我们所需要的是CP。

CP=AP*BP/AB=(|(Ax0+By0+C)/A|*|(Ax0+By0+C)/B|)/根号(|(Ax0+By0+C)/A|^2+|(Ax0+By0+C)/B|^2)

=|(Ax0+By0+C)^2/AB|/根号((Ax0+By0+C)^2*(A^2+B^2)/A^2*B^2)

=|(Ax0+By0+C)^2/AB|/[(Ax0+By0+C)/AB)*根号(A^2+B^2)]

=|Ax0+By0+C|/根号(A^2+B^2)

= |Ax0+By0+C|

-----------------

根号(A^2+B^2)

然后就显而易见了。对于每条直线，A，B，C是固定的，我们只需要提前求出Σx和Σy就行了。

所以

ans=min(

|AΣx+BΣy+C*n|

---------------

根号(A^2+B^2)

)

代码如下：

 1 #include<cmath>
 2 #include<cctype>
 3 #include<cstdio>
 4 #include<cstring>
 5 #include<algorithm>
 6 using namespace std;
 7 const int maxn=10005;
 8 struct point{
 9     int x,y;
10 }a[maxn],st[maxn];
11 struct line{
12     int A,B,C;
13 };
14 int n,len,Sum_x,Sum_y;
15 double ans;
16 inline int read(){
17     int x=0,f=1; char ch=getchar();
18     while (!isdigit(ch)){if (ch=='-') f=-f; ch=getchar();}
19     while (isdigit(ch)) x=x*10+ch-'0',ch=getchar();
20     return x*f;
21 }
22 point operator - (point a,point b){
23     point c; c.x=a.x-b.x,c.y=a.y-b.y;
24     return c;
25 }
26 double cross(point u,point v){
27     return (double)u.x*v.y-(double)v.x*u.y;
28 }
29 bool cmp(point u,point v){
30     if (u.x!=v.x) return u.x<v.x; else return u.y<v.y;
31 }
32 void Tubao(){
33     sort(a+1,a+n+1,cmp); len=0;
34     for (int i=1; i<=n; i++){
35         while (len>1&&cross(st[len]-st[len-1],a[i]-st[len-1])<=0) len--;
36         st[++len]=a[i];
37     }
38     int orilen=len;
39     for (int i=n-1; i>=1; i--){
40         while (len>orilen&&cross(st[len]-st[len-1],a[i]-st[len-1])<=0) len--;
41         st[++len]=a[i];
42     }
43 }
44 double abso(double x){
45     return x<0?-x:x;
46 }
47 line getline(point u,point v){
48     line li; li.A=v.y-u.y,li.B=u.x-v.x,li.C=v.x*u.y-u.x*v.y;
49     return li;
50 }
51 double calc(line li){
52     double v;
53     if (li.A!=0&&li.B!=0){
54         double v1=abso((double)li.A*Sum_x+(double)li.B*Sum_y+(double)li.C*n),v2=sqrt((double)li.A*li.A+(double)li.B*li.B);
55         v=v1/v2;
56     }else
57     if (li.A==0){
58         v=abso((double)Sum_y-(double)n*(-li.C)/li.B);
59     }else
60     if (li.B==0){
61         v=abso((double)Sum_x-(double)n*(-li.C)/li.A);
62     }
63     return v;
64 }
65 int main(){
66     int T=read();
67     for (int kase=1; kase<=T; kase++){
68         n=read(),Sum_x=Sum_y=len=0,ans=1e18,memset(a,0,sizeof a),memset(st,0,sizeof st);
69         for (int i=1; i<=n; i++){
70             int x=read(),y=read();
71             a[i].x=x,a[i].y=y,Sum_x+=x,Sum_y+=y;
72         }
73         if (n<=2){printf("Case #%d: %.3f\n",kase,0.000); continue;}
74         Tubao();
75         for (int i=1; i<len; i++){
76             line li=getline(st[i],st[i+1]);    ans=min(ans,calc(li));
77         }
78         printf("Case #%d: %.3f\n",kase,ans/(double)n);
79     }
80     return 0;
81 }

View Code

转载于:https://www.cnblogs.com/whc200305/p/7076766.html