机器学习性能评估指标之F1分数（F1 Score）

F值（F-Measure），也称为F1分数（F1 Score），是分类任务中用于综合评估模型精确率（Precision）​和召回率（Recall）​的指标，尤其适用于类别不平衡的场景。以下是关于F值的详细解析：

---

​一、F值的定义与公式

1. ​核心公式

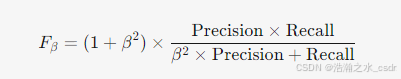
• ​默认形式（F1 Score）​：当 β=1 时，精确率和召回率的调和平均：

  

• ​β的意义：
  • β>1：更重视召回率（如疾病诊断）。
  • β<1：更重视精确率（如垃圾邮件分类）。

2. ​调和平均 vs 算术平均

• ​调和平均：对低值敏感，要求精确率和召回率均较高时F值才会高。
• ​算术平均：可能掩盖某一指标的低值（例如Precision=0.1，Recall=0.9时，算术平均=0.5，F1=0.18）。

---

​二、F值的适用场景

1. ​类别不平衡问题

• ​示例：欺诈检测（欺诈样本占1%），需平衡精确率（避免误判正常交易）和召回率（减少漏检欺诈）。
• ​优势：比单独使用准确率更能反映模型对少数类的识别能力。

2. ​需要权衡FP和FN的场景

• ​高FN代价：医疗诊断（漏诊患者风险高）→ 使用 β>1（如F2）。
• ​高FP代价：法律判决（误判无辜者风险高）→ 使用 β<1（如F0.5）。

3. ​多分类任务

• ​宏平均F1（Macro-F1）​：对每个类别的F1取平均，平等对待所有类别。
• ​微平均F1（Micro-F1）​：按样本权重计算全局F1，受大类别影响更大。

---

​三、F值的局限性

1. ​依赖阈值选择

• F值计算基于分类阈值（如0.5），不同阈值下F值可能变化显著。
• ​解决方法：结合PR曲线​（Precision-Recall Curve）观察不同阈值下的表现。

2. ​忽略绝对数值

• F值无法反映具体TP、FP的数量，需结合混淆矩阵分析具体错误类型。

3. ​对概率不敏感

• 若模型输出的概率未校准（如过于自信），F值可能无法反映真实性能差异。

---

​四、F值与其他指标的关系

​指标	​公式	​关注点
​精确率 (P)	TP/(TP+FP)	预测为正类的准确性
​召回率 (R)	TP/(TP+FN)	真实正类的覆盖率
​F1 Score	2×PxR/(P+R)​	平衡精确率与召回率
​Fβ Score	(1+β2)×P×R​/(βxβxP+R)	自定义权重平衡P和R

---

​五、代码示例（Python）​

from sklearn.metrics import f1_score, classification_report

# 真实标签和预测标签
y_true = [1, 0, 1, 1, 0, 1, 0]
y_pred = [1, 0, 0, 1, 1, 1, 0]

# 计算F1 Score
f1 = f1_score(y_true, y_pred)
print(f"F1 Score: {f1:.2f}")  # 输出: 0.75

# 多分类任务（宏平均与微平均）
y_true_multi = [0, 1, 2, 0, 1, 2]
y_pred_multi = [0, 2, 1, 0, 0, 1]

macro_f1 = f1_score(y_true_multi, y_pred_multi, average='macro')  # 宏平均
micro_f1 = f1_score(y_true_multi, y_pred_multi, average='micro')  # 微平均
print(f"宏平均F1: {macro_f1:.2f}, 微平均F1: {micro_f1:.2f}")

# 输出详细分类报告
print(classification_report(y_true, y_pred))

---

​六、实际应用案例

场景：新闻分类（3个类别：体育、科技、政治）

• ​模型A：宏平均F1=0.85，微平均F1=0.88（科技类别样本多，拉高微平均）。
• ​模型B：宏平均F1=0.90，微平均F1=0.87（各类别表现均衡）。
• ​选择依据：若需平等对待所有类别，选择模型B；若允许大类别主导，选择模型A。

---

​七、总结

• ​F值的核心作用：在精确率和召回率之间提供平衡，避免单一指标的片面性。
• ​使用建议：
  1. 类别不平衡时优先选择F1 Score。
  2. 根据业务需求调整β值（如F2或F0.5）。
  3. 结合混淆矩阵和PR曲线全面分析模型表现。
• ​局限性补充：对于概率敏感的模型（如风险预测），建议同时参考对数损失（Log Loss）​或校准曲线。

参考：

1. 机器学习：分类、多分类、回归模型的评估_多分类模型的评价标准-优快云博客